8．4．検定の例
8．4．1．母平均の検定
（1）両側検定の場合
製品をn=10個抜き取り、長さを測ったところ、平均\( \bar{X} \)=10.1cm、不偏分散から求めた標準偏差\( s \)=0.15cmだったとします。 このとき「製品の要求長さ10cm」に対して要求どおりといえるか？確認してみます。前提として、製品の長さは正規分布\( N(\mu,\sigma^2) \)に従い、5%の有意水準で検定を行います。
まず、仮説として「製品の長さは要求どおり10cmである」とします。 今わかっている平均10.1cm、標準偏差0.15cmは標本の値です。 このとき、次の統計量\( t \)は平均の推定（7.4.2節）で見たt分布に従います。
\[
t
=
\frac{ \bar{X} - \mu}{s/\sqrt{n}}
\]
そこでt分布表から、自由度9（=10-1）、片側2.5%（両側で5%）の値を拾ってくると、2.26になります。
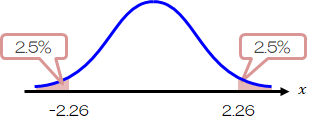次に、\( t \)の式にそれぞれの値を代入すると\( t=2.11 \)となり、\( -2.26 \leq t \leq 2.26 \)となるため棄却域に入りません。
\[
t
=
\frac{10.1-10 \quad }{0.15 / \sqrt{10} }
=2.11
\]
従って仮説は棄却できません
（ただし8.2節で見たように、製品は要求通りだ！と断言まではできません）。
（2）方側検定の場合
先ほどの例に対して、今度は「製品の長さを10cm以下にする」という要求にこたえられているか？を確認します。この場合も仮説として「製品の長さは10cmである」とします。
先ほどの例と異なるのは「10cm以上だと問題あり」になるので、右片側検定になることです。 従って、t分布表から自由度9（=10-1）、片側5%の値を拾ってくると、1.83になります。
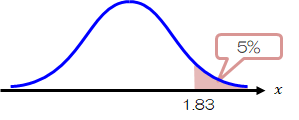\( t \)の値は先ほどと同じ\( t=2.11 \)なので、\( 1.83 \leq t \)となって、この場合は棄却域に入ります。
従ってこの場合、仮説は棄却され「製品の長さは要求どおりではない」と判断されます。
8．4．2．母分散の検定
例年収穫するいちご1粒の重さが平均\( mu \)=50g、標準偏差\( \sigma \)=5gだとします。 今年、25個のいちごの1粒の重さが平均\( \bar{X} \)=53gで標準偏差\( s \)=7gだったとすると、今年のいちごは例年と同じような粒ぞろいといえるでしょうか？前提として、いちごの重さは正規分布\( N(\mu,\sigma^2) \)に従い、5%の有意水準で検定を行います。
仮説として「例年どおり粒ぞろいである」とします。つまり母分散は\( \sigma^2 = 25 \)とします。 対立仮説として「\( \sigma^2 \neq 25 \)」とします。 このとき、次の統計量\( \chi^2 \)は分散の推定（7.4.3節）で見た\( \chi^2 \)分布に従います。
\[
\chi
=
\frac{(n-1) s^2}{\sigma^2}
\]
そこで\( \chi^2 \)分布表から、自由度24（=25-1）、片側2.5%（両側で5%）の値を拾ってくると、左側=12.4、右側=39.4になります。
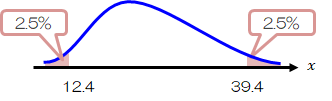次に、\( \chi^2 \)の式にそれぞれの値を代入すると\( \chi^2 =47.0 \)で、\( 39.4 \leq \chi^2 \)となり棄却域に入ります。
\[
\]
従って仮説は棄却され、今年のいちごはいつもよりも粒がばらついている、と判断します。
もし\( n=10 \)とすると\( \chi^2=17.6 \)となり、棄却域に対して\( 2.70 \leq \chi^2 \leq 19.0 \)となるため、仮説は棄却されません。 つまり、\( n \)数によって判断は変わる、ということになります。
