1．統計とは何か？
この章は“まえおき”なので、興味がなければ飛ばしてください。統計とは「着目している現象について調査し、数量として把握すること」です。 例えば、視聴率、選挙の投票率、平均身長、偏差値などがあてはまります。
統計学は「着目している現象を把握するために、集められたデータから現象の持つパターンや原因となる構造をあぶりだすこと」を目的とした学問です。
統計学によってあぶりだされた構造を知ることで、私たちは将来起こりうることについての予測が可能となります。 一番身近な例としては、選挙速報の結果が挙げられます （開票率0%なのになぜか当選確実、と出るのは統計学によるものです）。
統計学は、物理学、化学、経済学、社会学、心理学、工学、医学など、実証を必要とし、数値的根拠を指し示す必要のあるあらゆる分野で必要不可欠な学問となっています。
さて、統計を語る上で必要不可欠なのが“確率”です。
確率とは「出来事の起こりやすさを数値によって表す」ことを目的としています。 この確率が統計とどのように結びついているのか、以下に例を挙げて説明します。
統計ではデータを集めなければなりませんが、対象としている現象について、すべてのデータを揃えることは非常に困難（あるいは不可能）です。
例えば、20代日本人男性の平均身長を知るために、すべての人の身長を集めるのは不可能といっていいでしょう。 ではどうやって平均身長を知ることができるのか？というと、対象となる人の中から適当（ランダム）に1000人とか10000人を選び出し、その平均身長を求めることで、20代日本人男性の平均身長を推定する方法がとられます。
このとき、10000人全員の身長が極端に低い人ばかり集められる確率が極めて低いことは想像がつくと思います。 本来適当に選べば、身長の低い人から高い人までまんべんなく選ばれ、20代日本人男性全体の縮図がかなりの確率で再現されるはずです。
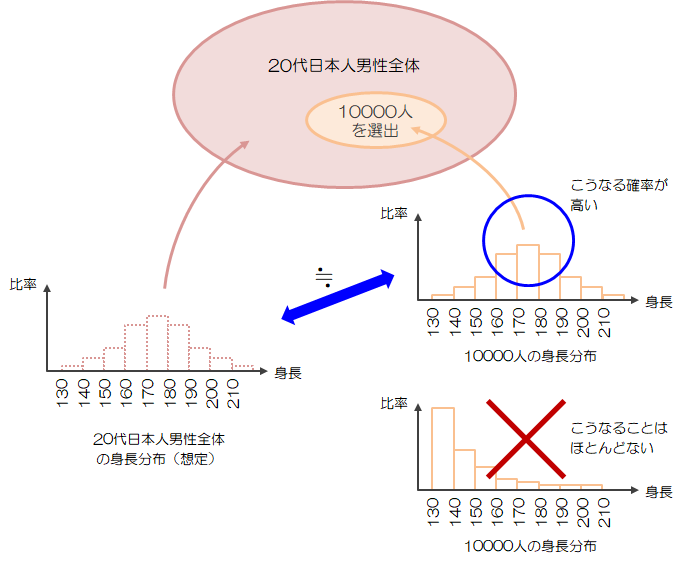ただし、全体を完全に再現した縮図とはならないため、いくらかの誤差を含みます。
また、別の10000人を選出した場合も平均にばらつきが生じます。
上記の説明は感覚的に過ぎますが、実際、全体の中からある程度の数を抽出すれば、その抽出分の平均が全体の平均として扱えることは、確率によって数学的に証明されています。 このように“統計”と“確率”は切っても切れない関係にあります。
