2．代表的な統計量
本章では、1クラス20人、A組～E組の5クラス分のテスト結果（100点満点）を例にとって説明していきます。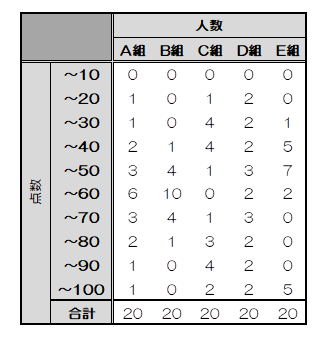
2．1．ヒストグラム
例えば、A組のテスト結果を10点刻みで集計してグラフ化してみます。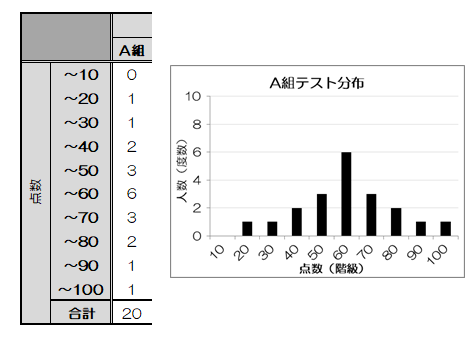
このとき、10点刻みの各段階を階級、各階級に含まれる人数（あるいは割合）を度数と呼びます。
この度数を縦軸、階級を横軸にとってグラフ化したものをヒストグラム（histogram）と呼びます。
グラフによってデータを視覚化することで、データの全体像、傾向を把握しやすくなります。
ヒストグラムは「データの分布状況を視覚的に把握する」のにうってつけの方法です。 しかしながら、階数の数や幅を適切にとらないと特徴が消えてしまい、データの性質をうまく取り出せなくなります （同じデータを50点刻みでグラフ化した場合）。
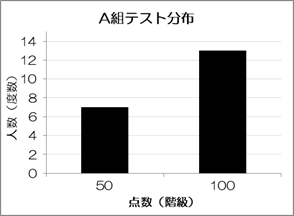またヒストグラムとは別に、階級が進むごとに度数を足し合わせて表現したグラフを累積度数図と呼びます。
ヒストグラムよりも累積度数図にした方がわかりやすいケースもあります。
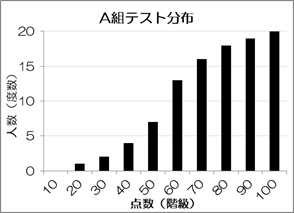せっかく例を挙げたので、5クラス分のヒストグラムを描いて見ます。
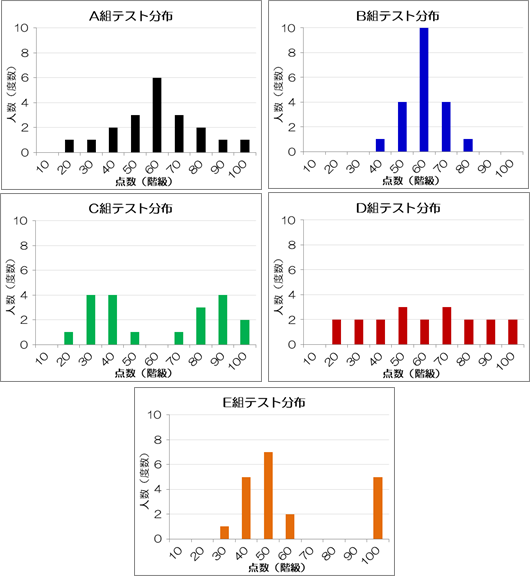すると、ヒストグラムから次のことがわかります。
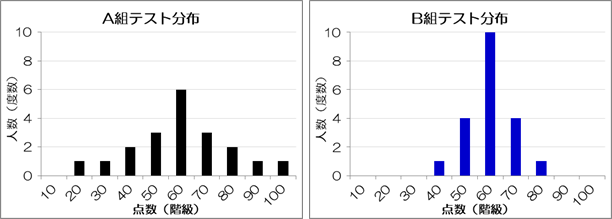
- A組とB組は60点あたりに人が集中しており、特にB組の人たちは学力が拮抗しています。
- C組とE組は、優秀な人たちとそうでない人たちに二分されています。 特にE組の優秀な人たちは極めて優秀です。
- D組は、優秀な人からそうでない人がまんべんなく集まっています。
2．2．平均・メジアン・モード
データを代表する主な値である “平均”、 “メジアン”、 “モード”の3つについて説明します。（1）平均（データの重心）
n個のデータ\(x_1,x_2,\cdots,x_n \)があるとき、平均\( \bar{x} \)は次のように計算します。\[
\bar{x}
=
\frac{x_1+x_2+\cdots+x_n}{n}
\]
各クラスのテスト結果の平均を計算すると、実はすべて60点になっています。
しかしヒストグラムをみると、その中身は違います。
A組、B組、D組のグラフは60点を境にほぼ対称形になっています。
C組、E組のグラフを見ると、60点の人はいないのに平均は60点です。 ただグラフを見ていると、やじろべぇのように60点を支点にして左右のバランスをとっているように見えます（つまり重心）。
以上のことから、平均は“データの重心”としての意味を持つことがわかります。
（2）メジアン（中央値または中位数）
データを小さい値から順に並べた真ん中の値のことをメジアンまたは中央値といい、算出方法は次のようになります。n個のデータ\(x_1 \leq x_2 \leq \cdots \leq x_n\)があるとき、
a）ｎが奇数の場合
\( n=2k+1 \)（\( k \)は自然数）で表せるので、\(x_1,\cdots, x_k, x_{k+1}, x_{k+2 \ } ,\cdots,x_n \)と並べれば、"\( x_{k+1} \)"がメジアン（中央値）になります（\( 1 \sim k \)で\( k \)個、\( k+2 \sim k+1 \)で\( k \)個）。
b）nが偶数の場合
\( n=2k \)となるので、\(x_1,\cdots, x_k, x_{k+1},\cdots,x_n \)と並べれば、\( 1 \sim k \)で\( k \)個、\( k+1 \sim n \)で\( k \)個となるので真ん中の値は1つに決まりません。
そこで\( n \)が偶数の場合は“\( x_k, x_{k+1} \ \)の平均=\( (x_k + x_{k+1})/2 \)”をメジアンとします。
ここで各クラスのテスト結果のメジアンを計算すると、A～D組は60点、E組は50点になります。
このことから、メジアンは平均と一致するわけではないことがわかります。
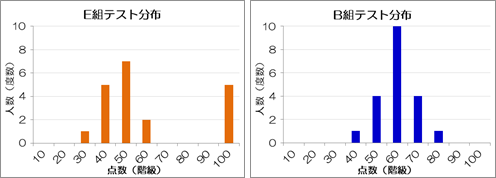
また、メジアンと平均が一致しないE組に着目します。
E組の中で極めて優秀なのは5人だけで、その他の15人は平均点以下です。 メジアンもまた平均より低い値を示しています。 ということは、E組は他のクラスと比較すると総じて学力は高くないことがわかります。 もし平均だけを見て評価すると、E組とB組は同程度の学力である、と誤った判断をしてしまいます。
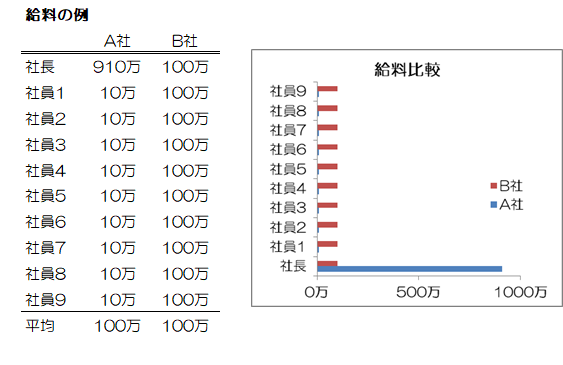
もっと極端な例を挙げれば、社員10人の会社で社長の給料だけ910万円、残りの従業員は10万円とします。
すると平均給料は100万円になりますが、決して従業員はいい生活が送れるわけではありません。
このときメジアンは10万円となり、E組の学力と同じようになります。
逆に社長も社員も給料が100万円なら平均もメジアンも100万円になり、B組の学力と同じになります。
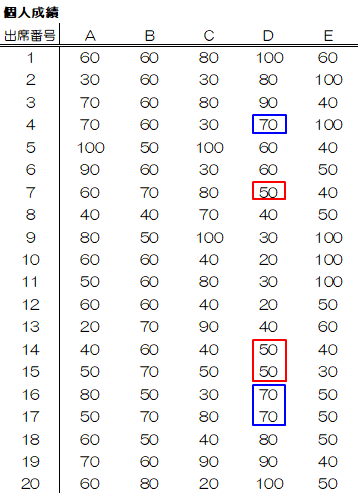
（3）モード（最頻値）
データの中で最も頻繁に現れる値のことをモードまたは最頻値といいます。モード（最頻値）は、値が1つとは限りません。 例えばD組でいえばモードは50点と70点の2つあります。
モードを用いるのに適しているケースは、メジアンの例で挙げた「社員10人の会社で社長の給料だけ910万円、残りの従業員は10万円」といった場合です。
このときの代表値を平均とすると100万円になりますが、これは実体と合いません。 この場合の代表値は最頻値である10万円とするのが適切でしょう。
このときの違いは何か、といえば分布のばらつき幅です。 そこで次節では、ばらつきの大きさを測る値について説明していきます。
2．3．分散・標準偏差
A組とB組は平均、メジアン、モードの値がすべて同じなのに、ヒストグラムの形は異なります。 A組は平均値からより遠くの点数まで幅広く分布しているのに対し、B組は平均値の周りに集中しています。 つまりA組とB組の点数には、ばらつきに差があることがわかります。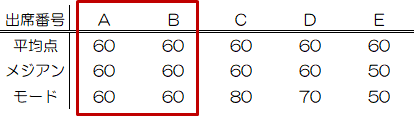
そこで本節では“ばらつき”を表す値について説明していきます。
まずは、A組とB組の各生徒の平均点との差=偏差を計算し、その平均をばらつきの尺度としてみましょう。
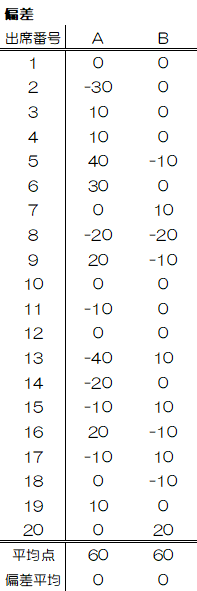すると、残念なことに偏差の平均はどちらも0になってしまいます。
これは偏差に正負の符号がつくからで、平均点はデータのバランス均衡点（重心）の意味を持つことからも、偏差平均\( \bar{a} \)が0になるのは当然の結果でしょう。
この結果は次の式変形からもわかります。
\[
\bar{a}
=
\frac{(x_1 - \bar{x}) + \cdots + (x_n - \bar{x})}{ n }
\]
この式を変形すると
\[
\bar{a} + \bar{x}
=
\frac{x_1 + \cdots + x_n}{ n }
\]
平均の式と比較すると、\( \bar{a} \)は必ず0でなければなりません。
この問題を解決するために偏差を二乗すれば、すべて0か正の値となり好都合です※。 偏差の二乗の平均を“分散”と呼びます。
※：正負の符号を消す方法として絶対値も使えるが、数学的に扱いづらい
\[
V
=
\frac{(x_1 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{ n }
\]
分散によってばらつきの大小を評価することはできますが、偏差を二乗しているため分散の単位は平均の単位の二乗となり、扱いづらさが残ります。
そこで分散の平方根をとった“標準偏差”をデータ分析で用いるのが一般的です。
\[
\sigma
=
\sqrt{ V }
=
\sqrt{
\frac{(x_1 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{ n }
}
\]
早速A組とB組（ついでにC～E組）の標準偏差を計算してみると、次のようになります。
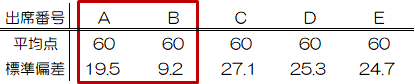標準偏差は“A組> B組”となって、ヒストグラムの分布の違いと一致する結果が得られました。
ところで、分散や標準偏差の計算式でよくみられるのが分母をn-1にした式
\[
\sigma
=
\sqrt{ V }
=
\sqrt{
\frac{(x_1 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{ n - 1 }
}
\]
です。分母にn-1をとる理由は後ほど（6.2.3節の不偏分散）説明しますのでしばらくお待ちください。
以上、統計の代表値として、分布の形を表す“ヒストグラム”、中心的な意味を表す“平均”“メジアン”“モード”、ばらつきを表す“分散”“標準偏差”について説明しました。
データ分析を行う上でこれらの値は非常に重要な役割を持ちますので十分理解し、活用できるようになっておく必要があります。
あと、数学的な表記にも慣れておく必要があります。 多数のデータの和はΣ記号を用いて表すのが一般的です。
あと、数学的な表記にも慣れておく必要があります。 多数のデータの和はΣ記号を用いて表すのが一般的です。
\[
\sum_{i=1}^{n} {x_i}
=
\frac{x_1 + \cdots + x_n}{ n - 1 }
\]
平均、標準偏差をΣ記号を用いて表すと、次のようになります。
\[
\begin{eqnarray}
& \bar{x}
& =
\frac{ \sum{ x_i }}{ n }
\\
& \sigma
& =
\sqrt{
\frac{ \sum{(x_i - \bar{x})^2}}{ n }
}
\end{eqnarray}
\]
