4．3．試行と事象
確率の話を理解する上で、次の二つの言葉を知っておく必要があります。- 試行：同じ条件のもとで繰り返すことができ、偶然によって決まる実験や観測
- 事象：試行の結果として起こる事柄
ここで、事象と前節の集合との対比を行います。
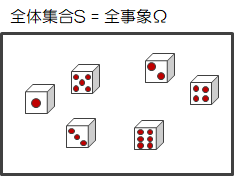
サイコロを1回振ったときに出る目の全事象\( \Omega \)は{1,2,3,4,5,6｝であり、前節の全体集合\( S \)と一致します。
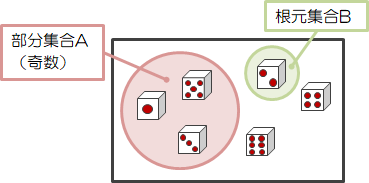
次に、奇数が出る事象\( A \)は{1,3,5}であり、前節の部分集合\( A \)と一致します。
同様に{2}が出る事象\( B \)は根元集合\( B \)と一致します。 特にこの場合の事象を根元事象と呼びます。
さらに、決して起こらない事象を空事象と呼び、これは空集合と一致します。
上図の\( A \cap B \)がこれに相当します。
このように事象\( A \)と事象\( B \)が決して同時に起こりえないとき、\( A \)と\( B \)は互いに排反である、といいます。
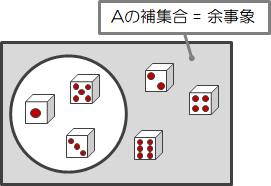
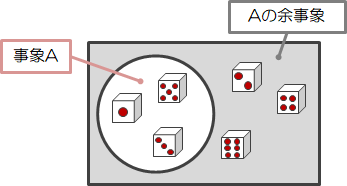
最後に、奇数が出ない事象は\( A \)でない集合、つまり前節でいう\( A \)の補集合と一致します。 このような事象を余事象と呼びます。
このように、事象と集合は次のような対応関係にあります。
- 全体集合\( S \) ⇔ 全事象\( \Omega \)
- 部分集合\( A \) ⇔ 事象\( A \)
- 根源集合\( B \) ⇔ 根元事象\( B \)
- 空集合\( \phi \) ⇔ 空事象
- 補集合\( A^c \) ⇔ 余事象
4．4．確率の定義
4．1節ですでに確率とは何か？について簡単に説明しています。 本節では、より数学的な確率の定義についてお話しします。“確率”とは「ある事象の発生割合」を表すもので、「対象としている事象に含まれる根元事象の数\( n(A) \)を、全事象に含まれる根元事象の数\( n(\Omega) \)で割ったもの」として定義されます。 なお、事象\( A \)の起こる確率は一般に\( P(A) \)で表します。
\[
P(A)
=
\frac{n(A)}{n(\Omega)}
\]
またまたサイコロを1回振ったときに出る目の確率を例にとって話を進めます。
まず、2が出る事象\( B \)の発生確率\( P(B) \)はいくらになるでしょうか？
全事象\( \Omega \)に含まれる根元事象の数（=サイコロの目の数）は6個あるので、\( n(\Omega)=6 \)になります。 この中から「2」という根元事象を1つを選び出すので、\( n(B)=1 \)になります。
従って確率\( P(B) \)は
\[
P(B)
=
\frac{n(B)}{n(\Omega)}
=
\frac{1}{6}
\]
になります。
当然、1, 3, 4, 5, 6の出る確率もすべて1/6になります。
次に、サイコロの目が奇数となる事象\( A \)の発生確率\( P(A) \)はいくらになるでしょうか？
奇数の出る事象\( A \)に含まれる根元事象は{1, 3, 5}の3個ですから、\( n(A) = 3 \)になります。
従って確率\( P(A) \)は、
\[
P(A)
=
\frac{n(A)}{n(\Omega)}
=
\frac{3}{6}
=
\frac{1}{2}
\]
になります。
さて、確率は取りうる値に範囲があります。 それは、空事象の発生する確率から全事象の発生する確率の間を取る、ということです。 具体的に言えば、確率\( P(A) \)の値は
\( 0 \leq P(A) \leq 1 \)
の間に必ず存在します。 空事象に含まれる根元事象の数は\( n(\phi)=0 \)なので\( P(\phi)=0 \)になります。全事象の確率は\( P(S)=n(\phi)/n(\phi)=1 \)になります。
今度は複数の事象に関する確率について見ていきましょう。
「サイコロを1回振る」の例で、事象\( A \)と事象\( B \)は同時に発生しないので、排反事象になります。 つまり、\( A\ \cap B= \phi \)（空事象）です。
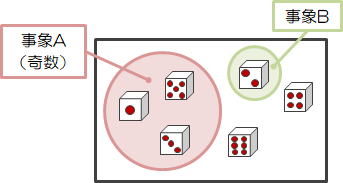このとき、事象\( A \)または\( B \)が起きる確率\( P(A \cup B) \)を求めてみましょう。
このとき\( n(A)=3, n(B)=1 \)です。 さらに上図からわかるように、\( n(A \cup B)=n(A) + n(B) \)が成り立つので、\( n(A \cup B)=4 \)になります。 全体事象\( n(\Omega) = 6 \)は変わりませんので、
\[
P(A \cup B)
=
\frac{n(A \cup B)}{n(\Omega)}
\]
になります。
この式は、次のように変形できます。
\[
\begin{eqnarray}
P(A \cup B)
& = &
\frac{n(A \cup B)}{n(\Omega)}
\\
& = &
\frac{n(A) + n(B)}{n(\Omega)}
\\
& = &
\frac{n(A)}{n(\Omega)} + \frac{n(B)}{n(\Omega)}
\\
& = &
P(A) + P(B)
\end{eqnarray}
\]
このように、排反事象の場合“\( P(A \cup B)=P(A)+P(B) \)”が成り立ち、これを確率の加法定理と呼びます。
次に余事象の確率について計算してみます。
\( A \)の余事象\( A^c \)が\( A \)と排反の関係にあることは、ベン図を見ると明らかです。
従って、
\( P(A \cup A^c)=P(A)+P(A^c) \)
となります。 ところで\( \Omega = A \cup A^c \)なので、\( P(A \cup A^c)=1 \)です。 従って、\( P(A^c)=1-P(A) \)
が成り立ちます。ここでは、排反事象における\( P(A \cup B) \)の確率を計算する方法についてみてきました。 となれば\( P(A \cap B) \)の確率はどうなるの？と疑問を持つかと思います。 これについては次節で見ていくことにします。
4．5．独立事象
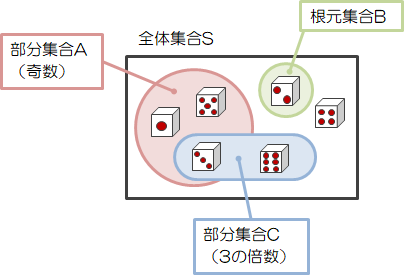
ここでは、次のような例を考えてみます。サイコロを1回振ったとき「奇数の目が出て、それが3の倍数である確率」を求めてみましょう。
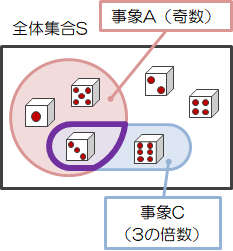これは「事象\( A \)が起きたときに事象\( C \)が起こる確率」、言い換えると「事象\( A \)の中で事象\( A \cap C \)が起こる確率」を求める問題になります。
このような問題を“条件付き確率”といい、\( P(C|A) \)で表します。これは次の関係式で表せます。
\[
P(C|A)
=
\frac{n(A \cap C)}{n(A)}
\]
なお、\( n(*) \)は事象*に含まれる根元事象の数です。
このケースでは\( n(A)=3, n(A \cap C)=1 \)なので、\( P(C|A)=1/3 \)になります。
さて、この\( P(C|A) \)は次のように変形できます。
\[
\begin{eqnarray}
P(C|A)
& = &
\frac{n(A \cap C)}{n(A)}
\\
& = &
\frac{P(A \cap C)}{P(A)}
\end{eqnarray}
\]
\[
\Leftrightarrow \
P(A \cap C)
=
P(C|A) \times P(A)
\]
この関係式を確率の乗法定理といいます。
先ほどの例をこの乗法定理を用いて計算してみます。
ベン図から\( n(C \cap A)=1 \)なので
\[
P(C \cap A)
=
\frac{n(A \cap C)}{n(\Omega)}
=
\frac{1}{6}
\]
\( n(A)=n(A)/n(\Omega)=3 \)なので\( P(A)=1/2 \)となって、
\[
P(C|A)
=
\frac{P(A \cap C)}{P(A)}
=
\frac{1/6}{1/2}
=
\frac{1}{3}
\]
が得られ、結果は一致します。
このとき実は「事象\( A \)の確率と事象\( C \)の確率は互いに影響を及ぼさない」、つまり「事象\( A \)の確率は事象\( C \)に関係なく決まり、事象\( C \)の確率も事象\( A \)に関係なく決まる」という前提に立っています。 これを“独立事象”と呼びます。
乗法定理“\( P(A \cap C) = P(C|A)×P(A) \)”が成り立つには、“\( A \)と\( C \)が独立”であることが条件です。
4．6．重複事象
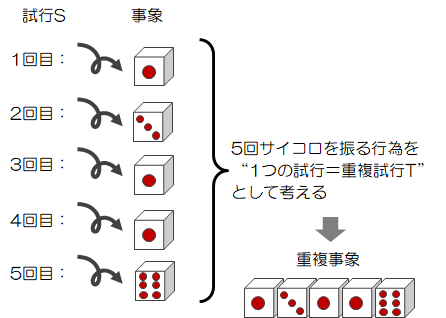
今度は、サイコロを5回振ったとき「1の目が3回出る確率」を求めてみましょう。ちょっとややこしいですが、次のように考えます。
- 「サイコロを1回振る」試行\( S \)において、「1の目が出る」事象\( A \)の確率を\( P(A) \)とします。
- \( S \)を5回繰り返し行います。 このように同じ試行を繰り返す行為を重複試行と呼びます。 今回はこの重複試行を\( T \)とします。
- \( T \)において「1の目が3回出る確率」事象\( B \)の生じる確率\( P(B) \)を求めます。 このときの事象\( B \)を重複事象と呼びます。
サイコロを1回振って出る目は、それぞれ独立に決まります。
従って、乗法定理が成り立ちます。
1回振ったときに1の目が出る確率は\( P(A)=1/6 \)ですので、これが3回出る確率は(1/6)3、残り2回は1以外の目が出る確率で(5/6)2になります。
ただし、5回のうちどのタイミングで1が5回出るかは指定されていません。
つまり、どこで1が出ても構いません。
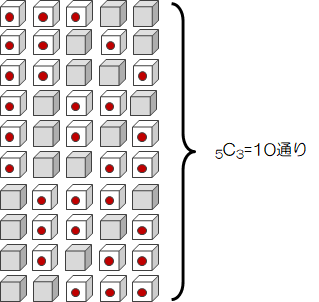
従って、5回中3回1が出る組み合わせは\( {}_5 C_3 = 10 \)通りになります。
以上から、
\[
P(B)
=
{}_5 \mathrm{C}_3 \times \left( \frac{1}{6} \right)^3 \times \left( \frac{5}{6} \right)^2
=
10 \times \frac{25}{6^5}
=
\frac{128}{3888}
\]
になります。
ここで重複事象の確率計算を一般化すると、次のようになります。
くどいですが細かく説明すると、
- ある試行\( S \)に伴う事象を\( A \)とします。
- \( S \)を複数回（全部で\( n \)回）繰り返し行い、重複事象\( T \)とします。
- 試行Tのうち、\( A \)が\( k \)回起きる事象を\( B \)とします。 このとき、\( B \)には\( A \)が起きない事象が\( (n-k) \)回含まれます。
\[
P(B)
=
{}_nC_k \times P(A)^k \times (1-P(A))^{n-k}
\]
