8．検定
8．1．検定とは？
コイントスを例に検定の話をします。1枚のコインを10回トスしたら8回“表”が出ました。
あなたならこれを“偶然”と考えますか？それとも“いかさま”と考えますか？
検証してみましょう（心の中では「“いかさま”やろ」と思ってください）。
まずは「“いかさま”はない」とする仮説を立てます（主張したいことと逆を仮説に立てます）。 この仮説を前提に10回中8回“表”が出る確率を計算します。 “いかさま”がなければ表の出る確率は1/2なので、二項分布により5.5%となります。
\[
\begin{eqnarray}
P(X \leq 8)
& = &
P(X=8) + P(X=9) + P(X=10)
\\
& = &
0.44 + 0.010 + 0.001
\\
& = &
0.055
\end{eqnarray}
\]
この“5.5%”を十分小さいと考えるなら「極めて稀なことが起きた」ことになります。
めったに起きないことが起きたんやから、これは“いかさま”や！！ということになります。
つまり、仮説である「“いかさま”はない」は間違っていると判断します。
このように検定は、
- ある仮説を立て
- その仮説を前提に、発生した事象の確率を計算し
- 確率が小さい場合は仮説を棄却し、そうでない場合は仮説を棄却しない
ところで、今回の例ではコイントス10回で“いかさま”のあるなしを判断しました。 しかし実際は、無限回コイントスをして表の出る確率が1/2かどうかを判断しなければなりません。 つまり、コイントス10回は“標本”であって、無限回のコイントスが“母集団”になります。
ということから、検定は「母集団に対する仮説を標本によって検証する作業」になります。
8．2．帰無仮説と対立仮説
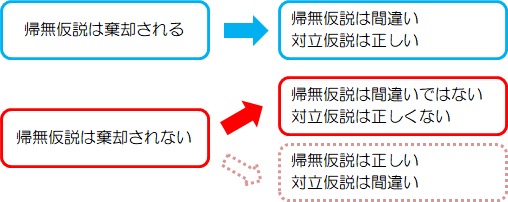
先ほどのコイントスで設定した仮説「“いかさま”はない」に対して、「“いかさま”はある」は対立しています。 設定した仮説を“帰無仮説”※、これと対立する仮説を“対立仮説”と呼びます。帰無仮説と対立仮説の間には互いに否定の関係にあり、次のようなマトリクスができます。
| 帰無仮説は正しい | 帰無仮説は正しくない 対立仮説は正しい |
|
|---|---|---|
| 帰無仮説を棄却しない | 〇 | × （第二種の誤り） |
| 帰無仮説を棄却する | × （第一種の誤り） |
〇 |
| ※： | 仮説は、コイントスの例でもあったように「主張したい結論の逆」をとるのが通例です。 棄却されることを想定して、「無に帰することを予定して」の意味を含んでいる“帰無”が仮説の前にくっついている、とイメージしてもらうのがよいでしょう。 ただし、常に無に帰するわけではないので“帰無”に深い意味はありません（帰無は省略することもあります）。 |
〇の部分は正しい判断となりますが、×については次のような意味合いがあります。
- 第一種の誤り：
- 正しいものを誤りと判断することで、例えば、良品を不良品と判断するような場合が該当します。
- 第二種の誤り：
- 誤りを正しいと判断することで、例えば、不良品を良品と判断するような場合が該当します。
8．3．仮説の棄却
検定では「仮説を棄却するか否か？」でその妥当性を判断します。そこで必要になるのが、仮説を棄却するかどうかを判断する閾値です。 先ほどのコイントスの例で5.5%を小さく見るには、何か基準となる値が必要です。 その基準となる閾値を“有意水準”あるいは“危険率”といい、一般に\( \alpha \)で表します （危険率という言い方は、「仮説は正しのに、それを棄ててしまう危険性は5.5%しかない」と言い換えられることからきています）。 有意水準は本来想定される値からのずれが「意味が有るほどずれているか？」という意味が込められています。
8.1節のコイントスの例に戻って、「“5.5%”を十分小さいと考えるなら」といいました。 これ、実に他人まかせな表現だと思いません？
実は、5.5%を小さいと判断する“有意水準”の決め方に決まりはありません。 目的や状況によって、有意水準を10%にしたり、1%にしたり、いろいろです。 有意水準を何%にするかは、その判断を必要とする人たち全員と手を握っておく必要があります。 ただ、有意水準を5%か1%にとることが一般的とされています。
あと仮説の棄却について、もう一つ知っておかなくてはならないことがあります。
それは“両側検定”と“片側検定”です。
例えば、仮説としておみくじで「大吉が10本入っている」としたとき、次の3つのパターンが考えられます。
- 大吉は10本入っていない → 10本かどうかを調べる
- 大吉は10本より多い → 10本より多いかを調べる
- 大吉は10本より少ない → 10本より少ないかを調べる
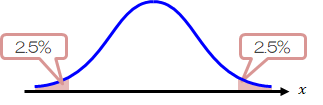
（1）は10 という値からどれくらい離れるか？が焦点になるため、左右両方に棄却域が現れます。 このとき、左右均等に2.5%の棄却域を設けます。 このような検定を“両側検定”といいます。
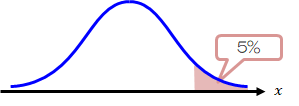
（2）は10より多い方が焦点になるため、右側に棄却域が現れます。
このような検定を“右片側検定”といいます（先ほどのコイントスの例はココに当てはまります）。
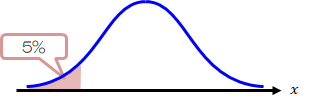
（3）は10より小さい方が焦点になるため、左側に棄却域が現れます。
このような検定を“左片側検定”といいます。
以上のように、どの検定を用いるかは、その目的と性質に応じて決める必要があります。
