7．4．推定の例
7．4．1．大標本での母平均の推定
例として、全国の中学3年生が受ける英語のテストの平均点について推定してみましょう。母集団は全国の中学3年生で、母平均を\( \mu \)、母分散を\( \sigma ^2 \)とします。
さて、標本として1000人を抽出し、その平均点\( \bar{X} \)が60点、不偏分散\( s ^2 \)から求めた標準偏差\( s \)が12点だったとします。 このときの95%信頼区間を求めます。
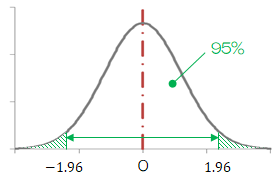
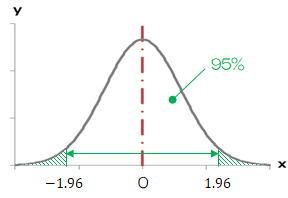
まず標本は十分大きいので、標本平均\( \bar{X} \)は正規分布\( N(\mu,\sigma ^2/n) \)に従います （6.2.2節）。 従って、信頼区間の幅は標準正規分布表※より\( P(-1.96 \leq Z \leq 1.96) = 0.95 \)を得ます （決まるのは1.96という値です）。
※：統計の教科書の巻末に掲載されています。
\( Z \)は標準正規変数で、確率変数\( \bar{X} \)（標本平均）、母平均\( \mu \)、母分散\( \sigma ^2 /n \)との間に以下の関係を持ちます。
\[
Z
=
\frac{ \bar{X} - \mu }{ \sigma / \sqrt{ n } }
\]
これを\( P(-1.96 \leq Z \leq 1.96) \)に代入すると信頼区間は
\[
\bar{X} - 1.96 \frac{ \sigma }{ \sqrt{n} }
\leq
\mu
\leq
\bar{X} + 1.96 \frac{ \sigma }{ \sqrt{n} }
\]
になります。
しかし残念なことに母分散\( \sigma \)は不明なため計算できません。
しかしながら\( n \)が十分大きい場合、母分散\( \sigma ^2 \)を不偏分散\( s ^2 \)で代用できるので、信頼区間を求めることができます。
\[
60 - 1.96 \frac{ 12 }{ \sqrt{1000} }
\leq
\mu
\leq
60 + 1.96 \frac{ 12 }{ \sqrt{1000} }
\]
\[
\because
59.3 \leq \mu \leq 60.7
\]
実はこの区間推定では母集団の分布に対して何も仮定していません。
制約としては「標本平均が正規分布に従えばよい」ということだけです。
7．4．2．小標本での母平均の推定
（1）では大標本（1000人）での推定を行いました。 この場合、標本平均が正規分布に従うことから信頼区間を求められました。しかし現実には大標本を得ることは簡単ではありません。 従って、小標本でも推定できることが望ましいといえます。
小標本で推定を行う場合「標本平均はt分布に従う」として区間推定を行います。 ただし（1）に対し、「母集団は正規分布に従う」という制約を付ける必要があります。
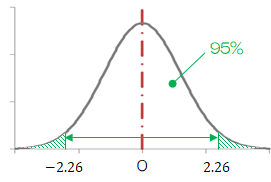
同じ例を使いますが、標本の大きさは10人とします（（1）は1000人）。 t分布の細かい説明は省きますが、t分布は標準正規分布の替わりとして使用し、不偏分散の自由度（標本の大きさ-1=9）をもとに信頼区間の幅が決まり、t分布表から\( P(-2.26 \leq t \leq 2.26) \)を得ます（自由度9、片側確率2.5%の値を拾います）。
ここからは（1）とほとんど同じです。
変数\( t \)は、確率変数\( \bar{X} \)（標本平均）、母平均\( \mu \)、不偏分散\( s^ 2/n \)との間に以下の関係を持ちます。
\[
t
=
\frac{ \bar{X} - \mu }{ s / \sqrt{ n } }
\]
これを\( P(-2.26 \leq t \leq 2.26) \)に代入すると信頼区間は
\[
\bar{X} - 2.26 \frac{ s}{ \sqrt{n} }
\leq
\mu
\leq
\bar{X} + 2.26 \frac{ s }{ \sqrt{n} }
\]
になりますので、\( \bar{X} = 60, s = 12, n = 10 \)を代入して95%信頼区間が計算できます。
\[
60 - 2.26 \frac{ 12 }{ \sqrt{10} }
\leq
\mu
\leq
60 + 2.26 \frac{ 12 }{ \sqrt{10} }
\]
\[
\because
51.4 \leq \mu \leq 68.6
\]
さて、（1）と（2）の違いは標本の大きさでした。
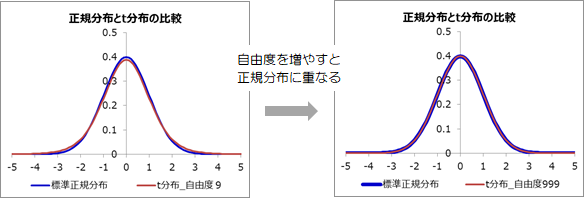
（2）はt分布を使うのに（1）は標準正規分布で良い理由は「標本が大きくなるほどt分布は標準正規分布に近づくため」です。
目安としては標本の大きさが30より小さければt分布を、それ以上の場合は標準正規分布を使います。
また（1）と（2）の結果を比べると、標本が大きいほど信頼区間は狭くなります。
- の結果：59.3≦μ≦60.7
- の結果：51.4≦μ≦68.6
7．4．3．母分散の推定
母分散の区間推定には、次に示す\( \chi ^2 \)分布を用います （（1）の標準正規分布、（2）のt分布と同じ役割を持ちます）。 母集団が正規分布に従うとき、大きさ\( n \)の標本から得られる不偏分散\( s^2 \)と母分散\( \sigma ^2 \)を含む変数\[
\chi ^2
=
\frac{ (n - 1) s^2}{ \sigma ^2 }
\tag{*}
\]
は自由度n-1（6.2.3節）の\( \chi ^2 \)分布に従います。
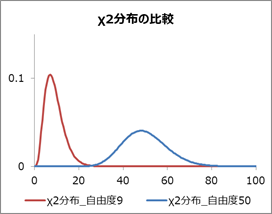負の方に分布がないのは\( \chi ^2 \gt 0 \)だからです。
ここで（2）の例を用いると、標本の大きさは\( n=10 \)なので自由度は\( n-1=9 \)になります。 （2）では母集団を正規分布としていますので、\( \chi ^2 \)分布が使えます。 今95%信頼区間を推定する場合、\( \chi ^2 \)分布表※から自由度9、確率5%の値を拾うことになります。 しかしながら、\( \chi ^2 \)分布はグラフからわかるように左右対称ではありません。 従って、左側2.5%、右側2.5%の値をそれぞれ\( \chi ^2 \)分布表から読み取る必要があります。 このとき左側は2.7、右側は19.0にります。
※：統計の教科書の巻末に掲載されています。
\[
P( 2.7 \leq \chi ^2 \leq 19.0)
=
0.95
\]
この\( \chi ^2 \)に（*）の関係式を代入すれば
\[
2.7 \frac{ \sigma ^2 }{ n-1 } \leq s^2 \leq 19.0 \frac{ \sigma ^2 }{ n-1 }
\]
\[
\Leftrightarrow
\quad
\frac{ n - 1 \ }{ 19.0 } s^2 \leq \sigma ^2 \leq \frac{ n - 1 \ }{ 2.7 } s^2
\]
となって、\( n=10, s=12 \)を代入して“\( 8.3 \leq \sigma \leq 21.9\)”を得ます。
ちなみに\( n=1000 \)で計算してみると“\( 11.5 \leq \sigma \leq 12.6\)”となって、信頼区間は大幅に狭まります。
7．4．4．二項分布の推定
視聴率\( p \)の推定をしてみましょう。少し前置きが長くなりますが、視聴率の定義とその特性について見ていきます。
視聴率\( p \)は、ある番組Aを見ているテレビの台数\( m \)の、全国すべてのテレビの台数\( N \)に対する割合です。
\[
p
=
\frac{m}{N}
\]
1家庭テレビ1台と仮定し、番組Aを見ているテレビの台数を確率変数\( X \)で表します。
視聴率\( p \)は次の理由から二項分布に従います。 各家庭は互いに影響を受けずに、番組Aを“見る”（確率=\( p \)）か“見ない”（確率=\( 1 - p \)）かの二択で決めています。 従って、番組Aを見ているテレビの台数が\( k \)のときの確率は、5.6節で見た二項分布\( B(n,p) \)に従います。
\[
P(X=k)
=
B(N,p)
=
{}_N C_k p^k (1-p)^{(N-k)}
\]
すると、番組Aを見ているテレビの台数の期待値μと標準偏差σは次のようになります。
\[
\begin{eqnarray}
\mu
& = &
np
\\
\sigma
& = &
\sqrt{Np(1-p)}
\end{eqnarray}
\]
さらにNが十分大きいとき、二項分布B(N,p)は正規分布N(μ,σ)で近似できます（5.6節）。
なお、推定したいのはpなので、μ、σとも推定するしかありません
（二項分布の母数は“p”ということです）。
以上を踏まえて、家庭数n=1000を対象に視聴率の標本調査を行います。
1000家庭の中から番組Aを見ているテレビの台数がkとなる確率P(X=k)は二項分布B(1000,p)に従います。
\[
\]
調査の結果、120の家庭で番組Aを見ていたとします（k=120）。すると標本内での視聴率p'は0.12となります。
また、今回の標本はn=1000と十分大きいため、二項分布B(1000,p)は正規分布N(μ,σ)で近似できるので、標本平均もまた正規分布に従います 。
ここで、信頼度95%で視聴率pの区間推定を行います。
標本の二項分布は正規分布で近似できることから、信頼区間の幅は標準正規分布表より\( P(-1.96 \leq Z \leq 1.96)=0.95 \)を得ます （決まるのは1.96という値です）。
標準正規変数\( Z \)は、確率変数\( X \)（番組Aを見ているテレビの台数）、母平均\( \mu = np \)、母分散\( \sigma^2 = np(1-p) \)との間に次式の関係を持ちます。
\[
Z
=
\frac{ X-np }{ \sqrt{ np(1-p) } }
\]
この\( Z \)を\( -1.96 \leq Z \leq 1.96 \)に代入すると、95%信頼区間の条件式が得られます。
\[
X - 1.96 \sqrt{ n p (1 - p) \quad }
\leq
\mu
\leq
X + 1.96 \sqrt{ n p (1 - p) \quad }
\]
ところで今推定したいのは視聴率\( p \)なので、両辺を\( n \)で割ると\( X/n \)は標本内の視聴率\( \hat{p} \)となるので、
\[
\hat{p} - 1.96 \sqrt{ \frac{ p (1 - p)}{n} \quad }
\leq
\mu
\leq
\hat{p} + 1.96 \sqrt{ \frac{ p (1 - p)}{n} \quad }
\]
が得られます。
しかし、ここまで来て残念なことに、上下信頼限界にともに視聴率\( p \)が含まれているため、信頼区間を計算できません。 ただし、今回は標本が十分大きいため、標本内の視聴率\( \hat{p} \)は大数の法則に従って母集団の視聴率\( p \)（母数）の点推定値として扱えます。 従って、\( \sqrt{ p(1-p)/n \quad } \)の\( p \)を、点推定の\( \hat{p} \)で置き換えて、さらに\( n=1000 \)、\( \hat{p} = 0.12 \)を代入すると、視聴率の区間推定を求めることができます。
\[
0.12-1.96 \times 0.01
\leq
p
\leq
0.12+1.96 \times 0.01
\]
\[
\because
0.10
\leq
p
\leq
0.14
\]
このように母集団が正規分布でなくても、正規分布で近似できるような場合は区間推定が可能になります。
7．4．5．推定実施の条件
区間推定を行う場合、いろいろな条件によって場合分けが必要になります。 そこで場合分けについての整理表を以下に示します （場合分けは、初学者向け用の範囲に限定します）。 なお、通常母集団分布や母分散\( \sigma \)はわかりませんが、母集団分布については経験的に判断されます。| 母集団分布 | 母分散 | 標本 サイズ |
標本平均 の分布 |
信頼区間 |
|---|---|---|---|---|
|
正規分布 \( N(\mu, \sigma) \) |
既知 | 正規分布 |
\[
\bar{X} - Z \displaystyle \frac{ \sigma }{ \sqrt{n} }
\leq
\mu
\leq
\bar{X} + Z \displaystyle \frac{ \sigma }{ \sqrt{n} }
\]
|
|
| 未知 | 大きい | 正規分布 |
\[
\bar{X} - Z \displaystyle \frac{ s }{ \sqrt{n} }
\leq
\mu
\leq
\bar{X} + Z \displaystyle \frac{ s }{ \sqrt{n} }
\]
|
|
| 小さい | t分布 |
\[
\bar{X} - t \displaystyle \frac{ s }{ \sqrt{n} }
\leq
\mu
\leq
\bar{X} + t \displaystyle \frac{ s }{ \sqrt{n} }
\]
|
||
|
二項分布 \( B(n, p) \) |
既知 | 大きい | ≒正規分布 |
\[
\hat{p} - Z \sqrt{\displaystyle \frac{ \hat{p}(1-\hat{p}) }{ n }}
\leq
p
\leq
\hat{p} + Z \sqrt{\displaystyle \frac{ \hat{p}(1-\hat{p}) }{ n }}
\]
|
