7．推定
7．1．統計学における推定
観測の対象を「統計学的に知る」とは[観測の対象となる母集団の性質を知ること]で、さらにはその「母集団の分布を知ること」に他なりません。 母集団の分布は6.2節で見たように母数で決まります。 しかしながら、この値を直接知ることは通常困難であり、推定するしかありません。統計学における推定は、母集団から無作為に抽出した標本の統計量から母数を推定することです （実はすでに6章で述べた内容そのままです）。
推定には次の二種類があります。
7．2．点推定
母平均を標本平均で推定する場合のように「母数の値を標本の統計量ズバリ1点で推定する」ことを“点推定”と呼びます。例えば母平均\( \mu \)を推定する場合、次のようになります。
- 大標本の場合、標本平均\( \bar{X} \)で推定（大数の法則） ：\( \mu = \bar{X} \)
- 標本平均\( \bar{X} \)の期待値\( E( \bar{X} ) \)で推定（6.2.1節） ：\( \mu = E( \bar{X} ) \)
\[
\sigma ^2
=
E(s^2)
\]
このように、点推定は値が1つに決まるのでわかりやすいのですが、欠点もあります。
推定には確率的な意味合いが含まれており、標本の抽出の仕方によって推定値はばらつきます。 標本平均\( \bar{X} \)の分散が\( V( \bar{X} ) = \sigma ^2 /n \)であることから（6.2.2節）、標本の大きさは小さいほど推定値のばらつきが大きくなり、母数の真値から外れる可能性が高くなります。 従って、その推定値の確からしさがわからないのが点推定の欠点です。
7．3．区間推定
“区間推定”は「母数の真の値が含まれる区間\( [L,U] \)を、ある確率\( \alpha ' \)%の範囲で推定する」ことです。 例えば、母平均\( \mu \)が\( L \leq \mu \leq U \)の範囲に入る確率が\( \alpha ' \)%である、という風に推定され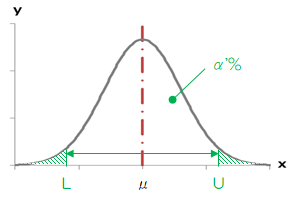ます。
\( \alpha ' \)は目的に応じて95%だったり99%といった値を使用するのが一般的です。
この\( \alpha ' \)を信頼度または信頼係数と呼びます。
また、区間\( [L,U] \)を信頼度\( \alpha ' \)%の信頼区間といい、\( L \)を下側信頼限界、\( U \)を上側信頼限界といいます。
区間推定では\( L \)と\( U \)、つまり信頼区間を推定します。 従って、標本の抽出の仕方によって信頼区間はばらつきます。 例えば信頼度95%だとすると、推定した100個の区間のうち、母平均\( \mu \)が信頼区間\( [L,U] \)に含まれるのはそのうち95個程度である、というのが区間推定の持つ意味になります。
