5．5．正規分布
これまでの話があってようやく「正規分布とは何か？」について話すことができます。さまざまな実験や観測を行い得られたデータのヒストグラムは、そのデータ数を増やせば増やすほど正規分布に近づいていくため、統計学において正規分布は非常に重要な役割を担っています。
5．5．1．正規分布とは？
まずは“正規分布”とはどんな確率分布か？について話をします。“正規分布”は「連続値をとるデータが平均値の周りに集積する、左右対称な釣り鐘型の確率分布」で、下図のような連続的なグラフを示します。
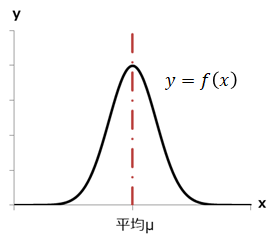
| ※： | 正規分布の導出は“わかりやすい”という部分から逸脱するため、説明は割愛しますが、誤差に関するガウスの公理を元に導出されます。 |
|
正規分布は連続型の確率分布のため、関数f(x)は確率密度関数になります。
正規分布の確率密度関数はデータの平均値μ、標準偏差σを用いて、以下の式で表します。
\[
f(x)
=
\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(x - \mu)^2}{2 \sigma^2}}
\]
なお、自然対数のべき乗は次のように表すこともできます（以降、expを用います）。
\[
e^x
=
\exp(x)
\]
正規分布には次のような特徴があります。
-
f(x)は標準偏差σで変曲点をとり、その大きさは分布の幅を決めるもので、大きいほど幅広い分布になります。
-
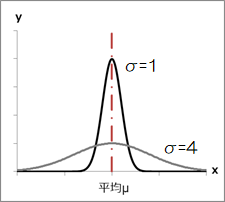
平均μの値に応じてf(x)はx軸方向に平行移動します。
-
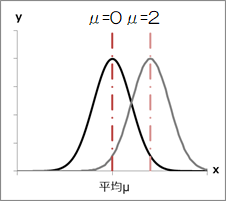
xがμ-σ≦x≦μ+σの範囲に入る確率は68.3%になります。
さらにxがμ±2σに入る確率は95.5%、μ±3σに入る確率は99.7%になります。
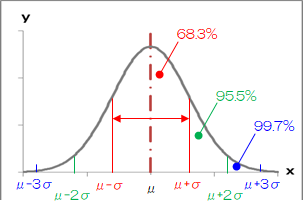
- 正規分布を-∞～+∞まで積分すると1になります。
5．5．2．標準正規分布
正規分布の特徴（1）、（2）から、任意の正規分布は平均μ=0、σ=1の正規分布に変換できます。 このμ=0、σ=1の正規分布を“標準正規分布”といいます。\[
f(x)
=
\frac{1}{\sqrt{2 \pi}} \exp \left( {-\frac{x^2}{2}} \right)
\]
標準化は次のようにして行います。
\( z=(x-\mu)/\sigma \)とおくと、\( \sigma dz=dx \)となるので、
\[
\frac{1}{\sqrt{2 \pi \sigma^2}}
\int_{-\infty}^{\infty} \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
=
\frac{1}{\sqrt{2 \pi}}
\int_{-\infty}^{\infty} \exp \left( {-\frac{z^2}{2}} \right) dz
\]
あらゆる正規分布は標準化できます。標準化する主な目的は次の通りです。
統計学の本では通常、巻末に標準正規分布表が添付されています。 この表から、確率変数の値がどのくらいの確率で出現するか？がわかります。 また、正規分布に従うデータどうしを比較する際、同じ土俵で比較できるようになります。
5．5．3．正規分布の期待値と分散
正規分布の期待値と分散を求めます。この時点でμ、σが何を表すかはわかっていません。そもそも平均と分散を使って正規分布を定義しているのに、この節の話に何の意味があるのか？と思う人もいるかと思います。 この節の目的は、正規分布関数に含まれる定数μとσが本当に平均と分散の意味を持つのか？というのを確認することです。 つまり、μとσはあくまで何らかの定数である、ということから始めて、この関数の期待値と分散を求めると、μとσになりました、ということが言えればよい、ということになります。
μとσが正規分布の平均と分散であることを問題なく受け入れる場合は、この節は読み飛ばしてください。
（1）正規分布の期待値
\[
\begin{eqnarray}
E(X)
& = &
\frac{1}{\sqrt{2 \pi \sigma^2}}
\int_{-\infty}^{\infty} x \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\\
& = &
\frac{1}{\sqrt{2 \pi \sigma^2}}
\int_{-\infty}^{\infty} (x -\mu + \mu) \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\\
& = &
\frac{1}{\sqrt{2 \pi}}
\int_{-\infty}^{\infty} \frac{(x -\mu)}{\sigma} \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\\
& \ & +
\frac{\mu}{\sqrt{2 \pi \sigma^2}}
\int_{-\infty}^{\infty} \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\end{eqnarray}
\]
ここで、第二項の積分は
\[
\int_{-\infty}^{\infty} \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
=
\sqrt{2 \pi \sigma^2}
\]
第一項の積分は、\( z=(x-\mu)/\sigma \)とおいて、\( \sigma dz=dx \)
\[
\begin{eqnarray}
& \ &
\frac{1}{\sqrt{2 \pi}}
\int_{-\infty}^{\infty} \frac{(x -\mu)}{\sigma} \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\\
& = &
\frac{1}{\sqrt{2 \pi}}
\int_{-\infty}^{\infty} \exp \left( {-\frac{z^2}{2}} \right) dz
\\
& = &
\left[
-\exp \left( -\frac{x^2}{2} \right)
\right]_{ \quad -\infty}^{ \quad \infty}
\\
& = &
0
\end{eqnarray}
\]
以上より、
\[
E(X)
=
0 + \frac{ \mu }{ \sqrt{ 2 \pi \sigma^2 }} \sqrt{ 2 \pi \sigma^2 }
=
\mu
\]
（2）正規分布の分散
\( V(X) = E(X^2) - \{E( \bar{X} )\} , E( \bar{X} )=\mu\)はわかっているので、ここでは\( E(X^2) \)を計算します。\[
E(X^2)
=
\frac{1}{\sqrt{2 \pi \sigma^2 }} \int_{-\infty}^{\infty} x^2 \exp \left\{ {-\frac{(x - \mu)^2}{2 \sigma^2} \ } \right\} dx
\]
\( z=(x-\mu)/\sigma \)とおいて、\( \sigma dz=dx \)から
\[
\]
第二項は積分=0、第三項は積分=\( \sqrt{2 \pi} \)
\[
\begin{eqnarray}
& \ &
\int_{-\infty}^{\infty} z^2 \exp \left( -\frac{x^2}{2} \right) dz
\\
& = &
\int_{-\infty}^{\infty} z \cdot z \exp \left( -\frac{x^2}{2} \right) dz
\\
& = &
\left[ -z \exp \left( -\frac{z^2}{2} \right) \right]_{\quad -\infty}^{\quad \infty}
+ \int_{-\infty}^{\infty} \exp \left( -\frac{x^2}{2} \right) dz
\\
& = &
\sqrt { 2 \pi }
\end{eqnarray}
\]
以上より、
\[
\begin{eqnarray}
E(X^2)
& = &
\sqrt{2 \pi} \frac{\sigma^2}{\sqrt{2 \pi}}
+ \frac{\mu-2}{\sqrt{2 \pi}} \sqrt{2 \pi}
\\
& = &
\sigma^2 + \mu^2
\end{eqnarray}
\]
従って、
\[
\begin{eqnarray}
V(X)
& = &
E(X^2)-\{ E(\bar{X}) \}^2
\\
& = &
\sigma^2 + \mu^2 - \mu^2
\\
& = &
\sigma^2
\end{eqnarray}
\]
5．6．二項分布
これまでは対象としている全事象の数が小さい例を扱ってきました。 しかし、現実には全事象の数が無数とも思えるほど大きな事象を扱うことが多々あります。 そこで本節では、全事象の数が大きくなる（無数になる）ようなケースについて説明します。ここでもまたサイコロの例で話を進めます。
まずは計算できる範囲で、サイコロを5回連続で振ったときに1の目が出る回数を確率変数Xとしたときの確率分布表を求めます （4.6節を参考にしてみてください）。
- P(X=0) = 5C0(5/6)5 = 0.40188
- P(X=1) = 5C1(1/6)(5/6)4 = 0.40188
- P(X=2) = 5C2(1/6)2(5/6)3 = 0.16075
- P(X=3) = 5C3(1/6)3(5/6)2 = 0.03215
- P(X=4) = 5C4(1/6)4(5/6)1 = 0.00322
- P(X=5) = 5C5(1/6)5 = 0.00013
P(X=k)=nCkpk(1-p)(n-k)
（n：サイコロを振る回数、k：1の目が出た回数、p：1の目が出る確率）
このような確率分布を二項分布と呼びます。 二項分布の確率は特に記号B(n,p)を用いて表現します。この計算式をもとに、n=10回、20回、50回、100回の確率分布を計算しグラフ化すると、下図のようになります。 また、各回数でのXの期待値は下表のとおりです。
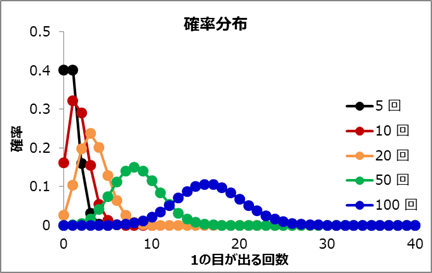上図を見ると、nを増やしていくごとに確率分布は期待値を中心に左右対称な形に近づいていくことがわかります（下図はn=100回）。
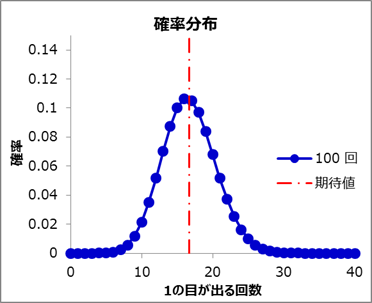二項分布は確率変数の数nはいくらでも増やすことができ、無数に増やすことも可能です。
また、nの数を増やすほど二項分布は正規分布に近づくため、n数が多い場合は正規分布で近似して計算を行うのが一般的です。
最後に、二項分布の期待値（平均）と分散の計算方法について説明しておきます（証明が不要な方は、式だけ確認してください）。
- 期待値：E(X)=np
- 分散 ：V(X)=np(1-p)
