4.1.確率とは?
まずは“確率”というものを感覚的につかむために、「サイコロを1回振ると何の目が出るか?」を例に見ていくことにします。サイコロに細工はなく、どの目も同じように出現するとします。 このとき、サイコロを1回振って2が出る割合はどの程度になるでしょうか?
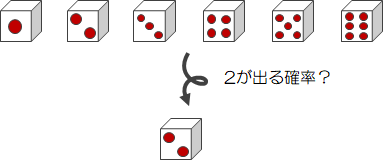 さいころの目は6個あるので、どの目が出るかは6通りあります。
その中で2が出るのは1通りだけです。
そこで、6通りの中から「2が出る」1通りの割合、つまり“1/6”を確率と呼びます。
さいころの目は6個あるので、どの目が出るかは6通りあります。
その中で2が出るのは1通りだけです。
そこで、6通りの中から「2が出る」1通りの割合、つまり“1/6”を確率と呼びます。
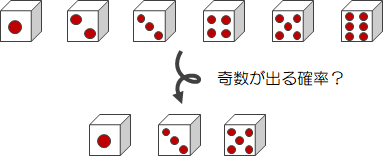
今度は、サイコロを1回振って奇数の目が出る確率はいくらになるでしょうか?
奇数のサイコロの目は1, 3, 5の3つです。 この3つならどれでもよいので、奇数の出る確率は、6通りの中から3通り発生する割合、「確率 = 3/6 = 1/2」になります。
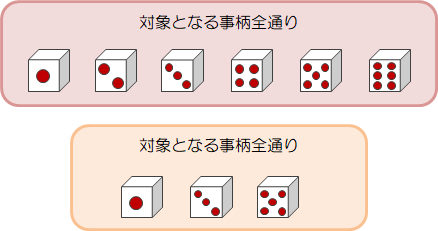
 このように確率は「対象となる事柄全通りのうち、着目している事柄が発生し得る割合」のことを言います。
このように確率は「対象となる事柄全通りのうち、着目している事柄が発生し得る割合」のことを言います。
 以上で、確率についての簡単な説明は終わりです。
ですが、これだけではもっと複雑な事柄に対する確率を求めることはできません
そこで次節からは、もう少し数学的な言葉を取り入れて、確率についての理解を深めていきましょう。
以上で、確率についての簡単な説明は終わりです。
ですが、これだけではもっと複雑な事柄に対する確率を求めることはできません
そこで次節からは、もう少し数学的な言葉を取り入れて、確率についての理解を深めていきましょう。
4.2.集合のはなし
“確率のはなし”なのに集合?となるかもしれませんが、確率は集合の概念があって成立するものです。 なので、集合について簡単に説明します。「ものの集まり」を集合といい、集合を構成する“もの”を元または要素といいます。
ただし集合は、元がその中に含まれているかどうかを明確に区別できなければなりません。 例えばサイコロの目は1, 2, 3, 4, 5, 6の数字が刻まれているので、1,…,6は集合の元、それ以外は集合に含まれないことがはっきりと区別できます。
 この場合{1, 2, 3, 4, 5, 6}はサイコロの目全体の集合となります。
このように、とりうる元すべての集合を全体集合と呼びます。
この場合{1, 2, 3, 4, 5, 6}はサイコロの目全体の集合となります。
このように、とりうる元すべての集合を全体集合と呼びます。
また{1, 3, 5}はサイコロの奇数の目の集合となります。 これは全体の中の部分的な集合になるので部分集合と呼びます。
さらに{1}, {2}, …, {6}のように1つの元で構成される集合を根元集合と呼びます (根元集合は部分集合の一部です)。
最後に{ }のように元を含まない集合も存在します。 これを空集合と呼びます。
集合を考えるとき、図式化すると便利です。
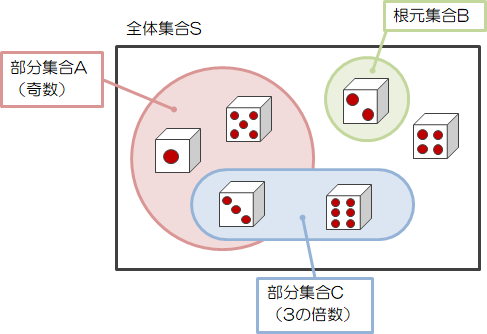 上図のように、複数の集合の関係や集合の範囲を図式化したものをベン図と呼びます。
上図のように、複数の集合の関係や集合の範囲を図式化したものをベン図と呼びます。
ベン図から次のような集合の存在が明らかになります。
(1)和集合
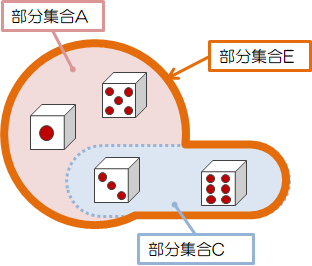
部分集合\( A \)の元と\( C \)の元をすべて含む集合\( E = \{1, 3, 5, 6 \} \)を作ることができます。 このように複数の集合の元をすべて含む部分集合を和集合と呼び、次のように表します。\( E = A \cup C \)(\( A \)または\( C \))
(2)積集合
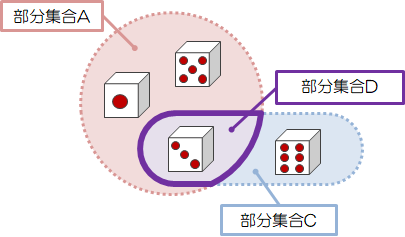
部分集合\( A = \{1, 3 ,5 \} \)(奇数)と\( C = \{3, 6 \} \)(3の倍数)の両方に属している元\( \{ 3 \} \)が存在し、部分集合\( D \)を作っています。 このように、複数の集合に同時に属する部分集合を積集合(共通集合)と呼び、次のように表します。\( D = A \cap C \)(\( A \)かつ\( C \))
(3)空集合
部分集合\( A \)と\( B \)の両方に属している元は存在しません。 つまり空の集合=空集合です。\( \phi = A \cap B \)
(4)差集合
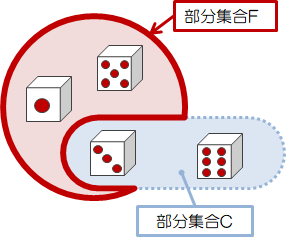
部分集合\( A \)から\( C \)に属する元を差し引いた部分集合\( F = \{1, 5 \} \)を作ることができます。 この\( F \を差集合と呼び、次のように表します。\( F = A - C \)
(5)補集合
全体集合\( S \)から部分集合\( E \)を差し引いた部分集合\( G = \{2, 4 \} \)は\( E \)でない集合でもあり、\( G \)を\( E \)の補集合と呼び、次のように表します。\( G = E^c \)
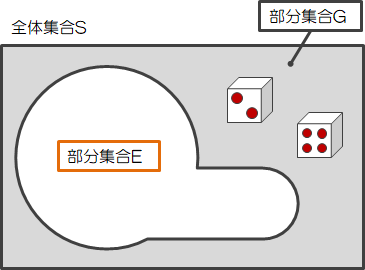 さて、“~でない”は文字の上に-をつけて表します。例えば、“\( E \)でない”は\( \overline{E} \)で表します。
従って、\( E \)の補集合\( G \)は
さて、“~でない”は文字の上に-をつけて表します。例えば、“\( E \)でない”は\( \overline{E} \)で表します。
従って、\( E \)の補集合\( G \)は
\( G = \overline{E} \)
でも表せます。(6)ド・モルガンの法則
ここで、集合の演算として“~でない”=否定の性質について見ていきます。補集合\( G \)の例をとれば“\( E \)でない”は“\( A \cup C \)でない”ということになります。
\[
\overline{E}
=
\overline{ A \cup C }
\]
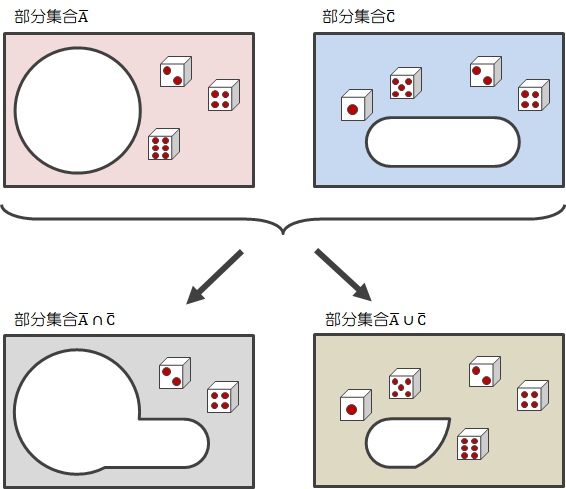
さらに、“\( A \cup C \)でない”は“\( A \)でない\( \cap \)(かつ)\( C \)でない”と言い換えられることは、ベン図を見るとわかります(下図右側)。
\[
\overline{ A \cup C}
=
\overline{A} \cap \overline{C}
\]
また、“\( A \cap C \)でない”は“\( A \)でない\( \cup \)(または)\( C \)でない”と言い換えられることも、ベン図をみればわかります(下図左側)。
\[
\overline{ A \cap C}
=
\overline{A} \cup \overline{C}
\]
このように、否定の中に\( \cap \)や\( \cup \)を含む場合、否定から出すとひっくり返ります。
- \( \overline{ \cap } \rightarrow \cup \)
- \( \overline{ \cup } \rightarrow \cap \)