3．相関
本章では、あるクラスの数学、国語、理科、社会のテスト結果から、それぞれの科目間に何らかの関係性があるか？を調べてみます。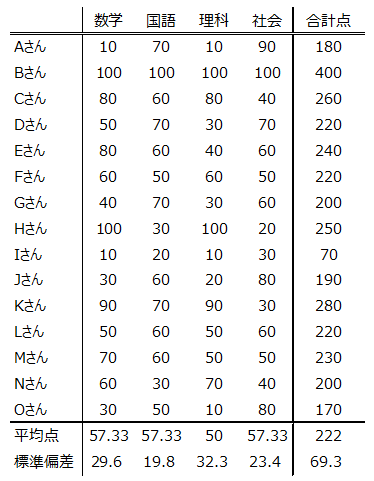
3．1．相関とは？
先ほどの点数表を見ただけでは正直何の傾向もつかめません。そこで“散布図”を利用して、それぞれの科目の結果をグラフ化＝視覚化してみます。
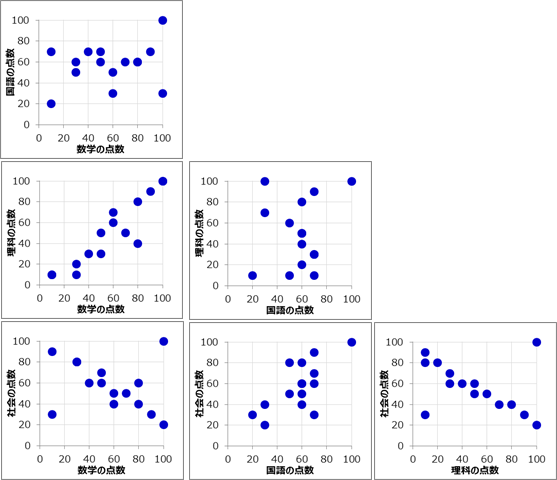散布図から、次の関係性が読み取れます。
- 数学の成績が良いほど、理科の成績も良い
- 国語の成績がよいほど、社会の成績も比較的良い
- 社会の成績が良いほど、数学と理科の成績は悪い
- 国語と数学、理科の間には傾向がみられない
さて、（1）と（2）は一方が増えれば他方も増える傾向にあり、これを“正の相関”といいます。 それに対し（3）は一方が増えれば他方は減る傾向にあり、これを“負の相関”といいます。
また、（4）のように一方の結果が他方に影響を及ぼさない場合を“無相関”といいます。
このように、一般に「両者の間に直線的な関係を持つ傾向がある」とき、“相関関係がある”といいます。
また、両者の関係が完全な直線であれば相関関係は強い、なんとなく直線的であれば相関関係は弱い、という風に表現します。
ただし、見た目の判断は、人によって主観の入る余地があり、客観性に乏しく、根拠薄弱です。
また、相関関係の強弱の判断もあいまいです。
そこで必要になるのが、相関の強さを表す値=“相関係数”になります。
3．2．相関係数
相関係数は相関の強さを表す値で、以下で定義されます。2種類の対応するデータをそれぞれ\( \{x_1, \cdots, x_n \}, \{y_1, \cdots, y_n \} \)、それぞれのデータの平均を\( \bar{x}, \bar{y} \)とするとき、相関係数\( r \)は次式になります。
\[
r
=
\frac{ \sum{(x_i - \bar{x})(y_i - \bar{y})} }
{ \sqrt{ \sum{(x_i - \bar{x})} \sum{(y_i - \bar{y})}}}
\]
ここで前節の点数表から各科目の間の相関係数を計算すると、次のようになります。
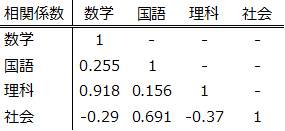同じ科目どうしの相関係数が1になるのはグラフを見れば明らかです。
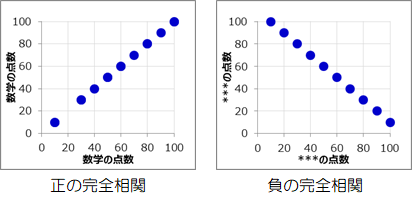
このように完全な正の直線関係をとるとき、“正の完全相関”と呼びます。
逆に相関係数が-1になるときは“負の完全相関”と呼びます。
前節の関係性が妥当か？を相関係数と照らし合わせて見てみます。
- 数学の成績が良いほど、理科の成績も良い
→ \( r = 0.92 \) - 国語の成績がよいほど、社会の成績も比較的良い
→ \( r = 0.69 \) - 社会の成績が良いほど、数学と理科の成績は悪い
→ \( r = -0.29 \)（社会と数学）、\( r = -0.37 \)（社会と理科） - 国語と数学、理科の間には傾向がみられない
→ \( r = 0.255 \)（国語と数学）、\( r = 0.156 \)（国語と理科）
3．3．相関関係と因果関係
相関関係と因果関係には大きな違いがあります。因果関係とは「二つ以上のデータの間に原因と結果の関係があること」です。 つまり因果関係においては、両者の連動についてきちんと理由を証明できなければなりません。 例えば、人口が増えればごみの量が増えるとか、犯罪が増える等があります。
それに対し相関関係は「二つ以上のデータの間に何等かの関係があること」です。 つまり、相関関係は何かしら傾向として両者が連動していることがわかっているだけです。 相関関係があるからといって因果関係があるとは限りません。 ごみの量が増えれば犯罪が増える、に直接的な因果関係はありませんよね。
なお、相関関係は因果関係を包含しています。
