6．母集団と標本
6．1．母集団と標本
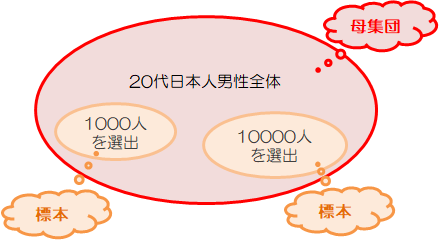
日本の成人男性の平均身長を調べるとしましょう。もし全員の身長を知ることができれば、平均身長は簡単に計算できます。 しかしながら、実際は骨折してまっすぐ立てない人、失踪して連絡がつかない人、誤って2回身長を測ってしまった人など、さまざまな要因で身長を正確に測れない人がたくさんいます。 それに、そもそも日本の成人男性はあまりにもたくさんいるので身長を測ること自体非常に困難です。 従って、全員の身長を知ることはほぼ不可能といっていいでしょう。
では、どうやって日本の成人男性の平均身長を知ることができるのでしょうか？
実際は、日本の成人男性の中から無作為（ランダム）に1000人とか10000人を選び出し、その平均を日本の成人男性の平均身長と推定する方法がとられます （この妥当性については後で説明します）。
このとき、「調査の対象となるもの全体」を“母集団”、そこから「分析のために抽出されたもの」を“標本”（サンプリング）と呼びます。 また、抽出した要素の数を標本の大きさといいます。 今の例では、日本の成人男性全員＝母集団、無作為に選びだされた1000人=標本、1000=標本の大きさになります。
また4.1節で見た集合でいえば、母集団=全体集合、標本=部分集合になります。
先ほどの例から言える重要なことは、私たちが知りえるのは標本の特性であって、母集団の特性はは推定するしかない、ということです。
なお、“母集団”と“標本”はここから先、何度も出てくる重要な言葉なので、ここでしっかりと覚えておいてください。
標本に関しては次の注意点があります。
標本は部分集合なので、抽出した要素1個のことも、1つのかたまり（部分集合の部分集合）も標本ということがあります。 そのため、標本が集団のことを指すか、要素のことを指すかは文脈から読み取る必要があります。
6．2．母数と統計量
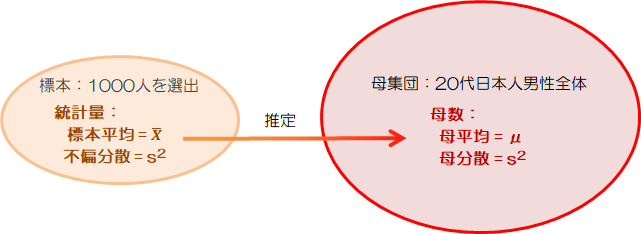
私たちは今、母集団の特性を知ろうとしています。統計学的に見て「母集団の性質を知る」とは「母集団の分布を知る」ことに他なりません。 もし母集団が正規分布なら、母集団の平均（母平均μ）と分散（母分散σ2）がわかれば、母集団分布を特定できます。 このように、母集団分布を特徴付ける定数を“母数”（パラメータ）といいます。
ただ前節で見たように、通常母集団の特性を直接知ることはできません。 例えば母平均や母分散を知るには、標本の平均（標本平均\( \bar{x} \)）や分散（不偏分散\( s^2 \)）から推定するしかありません。 このように、標本から計算される、母数の推定に使われる量を“統計量”と呼びます。
6．2．1．母平均と母分散
母集団の分布関数をf(x)で表すとき、母集団の平均（期待値）μと分散σ2は次式で計算できます （5.4節）。\[
\mu
=
E(X)
=
\left\{
\begin{eqnarray}
& \displaystyle \int_{-\infty}^{ \infty } x f(x) dx &
\quad （連続的）
\\
& \sum{x_i f(x_i)} &
\quad （離散的）
\end{eqnarray}
\right.
\]
\[
\sigma^2
=
V(X)
=
\left\{
\begin{eqnarray}
& \displaystyle \int_{-\infty}^{ \infty } (x - \mu)^2 f(x) dx &
\quad （連続的）
\\
& \sum{(x_i - \mu)^2 f(x_i)} &
\quad （離散的）
\end{eqnarray}
\right.
\]
この母集団の平均を母平均μ、分散を母分散σ2といいます。
6．2．2．標本平均
母集団から抽出したn個の標本\( X_1, X_2, …\cdots, X_n \)から得られる平均\( \bar{X} \)を標本平均といいます。\[
\bar{X}
=
\frac{X_1 + \cdots + X_n}{n}
=
\frac{1}{n}
\sum_{i=1}^n{X_i}
\]
標本平均\( \bar{X} \)は必ずしも母平均μとは一致しません。
例えば1～10の整数の平均を母平均と標本平均で比べてみます。
- 母平均：
\[ \mu=\frac{1+2+\cdots+9+10}{10}=5.5 \] - 標本平均：
\[ \begin{eqnarray} & \bar{X} &=\frac{1+5+10}{3}=5.3\cdots \\ & \bar{X} &=\frac{2+5+8}{3}=5.3\cdots \\ & \bar{X} &=\frac{1+2+9+10}{4}=5.5 \end{eqnarray} \]
それだと「母平均μは標本平均\( E( \bar{X}) \)から推定できないじゃないか！！」となりますが、ここで標本平均\( \bar{X} \)の期待値\( E( \bar{X}) \)を計算してみます。
各標本は母集団から抽出されたものなので、その期待値は\( E(X_i)=\mu \)となります。 それに加えて5.4節の性質を利用して\( E( \bar{X}) \)を計算すると、
\[
\begin{eqnarray}
E( \bar{X})
& = &
E \left( \frac{X_1 + \cdots + X_n}{n} \right)
\\
& = &
\frac{1}{n} E(X_1 + \cdots + X_n)
\\
& = &
\frac{1}{n} \{ E(X_1) + \cdots + E(X_n) \}
\\
& = &
\frac{ n \mu }{n}
\\
& = &
\mu
\end{eqnarray}
\]
となって、標本平均の期待値\( E( \bar{X}) \)は母平均μと一致します。
さらに、標本平均の分散\( V(\bar{X}) \)を求めてみます（標本分散ではありません）。
これも期待値同様、母分散をσ2とすると各標本の分散は\( V(X_i) = \sigma^2 \)となります。 それに加えて5.4節の性質を利用して\( V(\bar{X}) \)を計算すると、
\[
\begin{eqnarray}
V( \bar{X})
& = &
V \left( \frac{X_1 + \cdots + X_n}{n} \right)
\\
& = &
\frac{1}{n^2} V(X_1 + \cdots + X_n)
\\
& = &
\frac{1}{n^2} \{ V(X_1) + \cdots + V(X_n) \}
\\
& = &
\frac{ n \sigma^2 }{n^2}
\\
& = &
\frac{ \sigma^2 }{n}
\end{eqnarray}
\]
となります。標本の大きさnが大きくなるほど\( V(\bar{X}) \)は0に近づくので、標本平均\( E(\bar{X}) \)は母平均μに近づいていくことになります。
このように、標本平均\( \bar{X} \)自体は母平均μと一致するとは限りませんが、その期待値\( E(\bar{X}) \)は母平均μと一致します。
標本平均のように、標本から算出した推定量の期待値が母集団の期待値に一致するような量を“不偏推定量”といいます。
6．2．3．不偏分散
母集団の分散を知るには、標本の分散が前節でみた不偏推定量でなければなりません。 母集団から抽出したn個の標本X1、X2、…、Xnから得られる、不偏推定量となる分散s2を不偏分散といい、次式で表します（\( \bar{X} \)は標本平均）。\[
\begin{eqnarray}
s^2
& = &
\frac{1}{n-1}
\{
(X_1 - \bar{X} )^2 + (X_2 - \bar{X} )^2 + \cdots + (X_n - \bar{X} )^2
\}
\\
& = &
\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X} )^2
\end{eqnarray}
\]
不偏分散の特徴は、標本の大きさnではなくn-1で割っていることです。
ここで、s2が不偏推定量であること、つまりE(s2)=σ2を証明します
（s2がσ2と必ずしも一致するわけではありません）。
証明 **********
各標本は母集団に属するので、その期待値と分散は、
次に、Yi=Xi-μとおきます。 すると、次の関係式が得られます。
以上で、"s2"が不偏分散であることを証明できました。
E(Xi)=μ、V(Xi)=σ2
を満たします。また、標本はランダムに抽出されているので互いに独立である、と考えます。次に、Yi=Xi-μとおきます。 すると、次の関係式が得られます。
- \( E(Y_i) = E(X_i) - \mu = 0 \)
- \( E(\bar{Y}) = E \left( \displaystyle \frac{Y_1 + \cdots + Y_n}{n} \right) = 0 \)
- \( \bar{X} = \displaystyle \frac{X_1 + \cdots + X_n}{n} = \frac{Y_1 + \cdots + Y_n}{n} + \mu = \bar{Y} + \mu \)
- \( X_i - \bar{X} = (Y_i + \mu) - (\bar{Y} + \mu) = Y_i - \bar{Y} \)
- \( V(Y_i) = V(X_i - \mu) =V(X_i) = \sigma ^2 \)
- \( V(\bar{Y}) = V(\bar{X} - \mu) = V(\bar{X}) = \displaystyle \frac{\sigma^2}{n} \)
- \( V(Y_i) = E(Y_i^2) \)
- \( V(\bar{Y}) = E(\bar{Y}^2) \)
\[
\begin{eqnarray}
E(s^2)
& = &
E \left\{ \frac{\sum(X_i - \bar{X})^2}{n-1}\right\}
\\
& = &
\frac{E\{ \sum (Y_i - \bar{Y})^2 \}}{n-1}
\\
& = &
\frac{E\{ \sum (Y_i^2 - 2Y_i \bar{Y} + \bar{Y}^2) \} \quad}{n-1}
\\
& = &
\frac{E( \sum Y_i^2) - 2E( Y_i \bar{Y} ) + nE( \bar{Y}^2) \quad}{n-1}
\\
& = &
\frac{n \sigma^2 - 2nE( \bar{Y}^2 ) + nE( \bar{Y}^2) \quad}{n-1}
\\
& = &
\frac{1}{n-1} \left( n \sigma^2 - n \frac{\sigma^2}{n} \right)
\\
& = &
\sigma^2
\end{eqnarray}
\]
********** おわり
もし標本の分散に5.4節で定義した分散"S2"
\[
S^2
=
\frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X} )^2
\]
を用いると、その期待値E(S2)は
\[
E(S^2)
=
\frac{n - 1}{n} \sigma^2
\]
となり、nが小さいときにσ2の推定量を過小評価してしまいます。
ところで、不偏分散の分母n-1にどういった意味があるのでしょうか？
不偏分散の式に用いられる標本平均\( \bar{X} \)から次の関係式が得られます。
\[
(X_1 - \bar{X}) + (X_2 - \bar{X}) + \cdots + (X_n - \bar{X})
=
0
\]
これはn個の確率変数に対する拘束条件となっていて、\( (X_1 − \bar{X})、(X_2− \bar{X} ), \cdots \)を自由に動かすと、勝手に\( (X_n - \bar{X} ) \)が決まってしまいます。
\( \bar{X} \)は母平均μの推定量として代用しているので、拘束式がある分自由に動ける変数の数が減ってしまいます
（今回は1個）。
これがn-1の正体です。
このように、互いに自由に動ける変数の数を自由度と呼びます。
6．3．大数の法則と中心極限定理
ここでは統計学の基本定理となる“大数の法則”と“中心極限定理”がどういったものか？について紹介します。 次章以降の推定や検定の考え方の基礎となるものですので、知っておく必要があります。なお、どちらも証明可能な定理ですがここでは割愛します。興味のある方はWikipedia等を参考にしてください
大数の法則
大標本の平均\( \bar{X} \)は母集団の平均μとみなしてよく、母集団の分布にかかわらず成立します。中心極限定理
母集団の分布が何であっても、確率変数の和X1+X2+…+Xnの確率分布は、nが大きくなれば正規分布とみなせます。n個の確率変数の和
Sn=X1+X2+…+Xn
は、nが大きいとき正規分布に従う、と言っています。 ここでSnの両辺をnで割ると、\[
\bar{X}
=
\frac{S_n}{n}
\]
標本平均\( \bar{X} \)が得られるので、中心極限定理は「標本平均の確率分布はnが大きくなれば正規分布とみなしてよい」ということになります。
