gijyutsu-keisan.com

5．確率変数と確率分布

ここからいよいよ統計学の核心部に迫っていきます。
確率変数と確率分布は、統計学の醍醐味である推定や検定の根幹となる概念です。 また、正規分布は理論的にも実用的にも非常に重要で、統計学の中心的な役割を担っています。 ただ残念ながら、総和（Σ）や極限（微分積分）など、数学的に少し難しい表現が必要になってきます。 極力簡単にイメージできるよう、説明していきたいと思います。

5．1．確率変数と確率分布

ここでもサイコロの例を使って説明していきます。
サイコロを振ったときに出る目がいくつになるか？は、サイコロを振ってみないとわかりません。 つまり試行の前には決まらず、試行の結果によって決まります。
確率変数 中学の数学で「わからない値は文字＝変数で表す」と習ったと思います。 従ってサイコロの目は、試行前はいくつかわからないため、変数Xで表せます。
また、サイコロの目はそれぞれ確率1/6で現れます。 つまり、変数Xの値に対応する確率が存在します（下表参照）。
確率分布 このように、変数Xのとり得る値\(x_1, x_2, \cdots, x_n \)それぞれに、確率\(p_1, p_2, \cdots, p_n \)が与えられるとき、Xを“確率変数”といい、\(x_1, x_2, \cdots, x_n \)と\(p_1, p_2, \cdots, p_n \)の対応関係 = 関数を確率変数Xの“確率分布”といいます。
確率分布を関数で表せることは、後に非常に重要な意味を持ちます。
さて、確率分布には4.4節でみた確率の値に対する制約
  • 空事象の確率 = 0
  • 全事象の確率 = 1
から、次の条件を満たします。
\[ \begin{eqnarray} & p_1 \geq 0 &, p_2 \geq 0, \cdots, p_n \geq 0 \\ & \sum_{k=1}^n{p_k} & = p_1 + p_2 + \cdots + p_n =1 \end{eqnarray} \]
ここで、確率変数を使った確率計算の具体例を挙げておきます。
  1. サイコロの目が5となる確率
    \[ P(X=5) = \frac{1}{6} \]
  2. サイコロの目が2以下となる確率
    \[ \begin{eqnarray} & P(X\leq2) & = & P(X=1) + P(X=2) \\ & & = & \frac{1}{6} + \frac{1}{6} \\ & & = & \frac{1}{3} \end{eqnarray} \]
  3. サイコロの目が奇数になる確率
    \[ \begin{eqnarray} P(X mod 2 = 1) & = & P(X=1) + P(X=3) + P(X=5) \\ & = & \frac{1}{2} \end{eqnarray} \]
  4. 2回サイコロを振ったときの目の和が7になる確率
    \[ \begin{eqnarray} P(X_1+X_2=7) & = & P(X1=1, X2=6) + P(X1=6, X2=1) \\ & &+ P(X1=2, X2=5) + P(X1=5, X2=2) \\ & & + P(X1=3, X2=4) + P(X1=4, X2=3) \\ & = & \left( \frac{1}{6} \right)^2 \times 6 = 6/36 \end{eqnarray} \]

5．2．離散値と連続値

確率変数は、前節のサイコロの目以外にも、いろんな値をとることができます。
  1. サイコロを10回振ったときに1の目が出る回数
  2. 3つのサイコロを同時に振ったときのサイコロの目の和
  3. 日本男性の身長（180cm以上190cm以下など）
  4. 1年間の気温の変化

などなど


（1）や（2）のように確率変数の値が“とびとび”の場合を“離散値”、（3）や（4）のように任意の実数、つまり連続した値の場合を“連続値”といいます。
離散値と連続値 なお、離散値の場合でも、確率変数の取る値は無数に存在する場合があります（0～∞の整数など）。 連続値の場合は、範囲が限定されていても値は無数に存在します。

5．3．確率密度関数

次に、確率変数が離散型の場合と連続型の場合で、確率分布はどう変化するか？について見ていきます。

（1）離散型の確率分布

まずは離散型の確率分布について、5.1節の例を使って表すと次のようになります。
\[ P(X=x_k) = \left\{ \begin{eqnarray} & \frac{1}{6} & \quad (k=1,2,\cdots,6) \\ & 0 & \qquad (otherwise) \end{eqnarray} \right. \]
これを一般化すると次のようになります。
\[ P(X=x_k) = \left\{ \begin{eqnarray} & f(x_k) & \quad (k=1,2,\cdots) \\ & 0 & \quad (otherwise) \end{eqnarray} \right. \]
このとき、Xがaとbの間の値をとる確率は次のように計算できました。
\[ P(a \leq X \leq b) = \sum_{k=n_a}^{n_b}{f(x_k)} \qquad (x_{na}=a, x_{nb} = b) \]

（2）連続型の確率分布

離散型の場合、例えばサイコロの目のように確率変数が整数の場合、X=1、2、…に対応してP(X=1)=f(1)、P(X=2)=f(2)、…が決まりました。 しかし、Xが例えば身長のような連続型をとる場合、身長が180cmピッタリ、という人はこの世の中にはほとんどいないでしょう。 実際は180.1cmだったり、よ～く測ると179.9999998cmだったりするはずです。 となれば、P(X=180)≒0でなければなりません。 しかしf(180)=0だと、他の任意のXに対してもf(X)=0でなければならないので、確率分布は0になってしまいます。
連続型の確率分布 そこで、確率変数Xが連続型をとる場合は、次のように考えます。
下図のように関数f(x)をN個に区分けし、区分の幅をΔxとします。
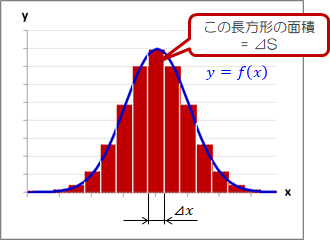連続型の確率分布 このとき、Δxが十分小さければ区分面積は以下で表せます。
\[ \Delta S \simeq f(x) \Delta x \]
この⊿Sをx～x+Δxの範囲の確率\( P(x \leq X \leq x + \Delta x ) = \Delta p \)と考えてみます。
\[ \Delta P = \Delta S \simeq f(x) \Delta x \]
すると、Δx > 0ならΔS > 0となって0でない確率が存在し、Δx→0とすればP(X=x)→0になり、身長が180cmピッタリの確率が0となる解釈と一致します。
ここで、連続型のP(a≦X≦b)の確率を次のようにして求めます。
まず、a～bの範囲をN個に区分けします。すると、区分1個の面積は次のようになります。
\[ \Delta S \simeq f(x) \Delta x = f(x) \frac{b-a}{N} \]
これをa～bの範囲分足し合わせるのですが、Δxのままでは離散型になってしまいます（Δx > 0）。 Xはあくまで連続型の変数ですから、Δx→0にするためにN→∞の極限をとる必要があります （区間を無数に細かくすれば、分割幅はおのずと0に近づいていきます）。 すると、総和の式は積分の式に変換され、
\[ P(a \leq X \leq b) = \displaystyle \lim_{ n \to \infty } \sum_{k=1}^N f(x_k) \Delta x = \int_a^b f(x) dx \]
になります。
確率変数Xが連続型のとき、関数f(x)は確率そのものを表すのではなく、単位面積当たりの確率＝“密度”を表している、と捉えることができます。
従って、確率変数が連続型のときの確率分布関数f(x)を“確率密度関数”と呼びます。

参考文献

▲