gijyutsu-keisan.com

2．6．締付トルクの算出

2．6．1．締付トルクの計算式

必要な軸力を得るには、ボルトを締め付けなければなりません。 このとき、座面とねじ面の摩擦力によって軸力が得られます。 この摩擦力によって発生する、座面に作用する摩擦トルク\(T_{fl} \ \)とねじ部に作用する摩擦トルク\(T_{th} \ \)の合計で締付トルク\(T_f \ \)が決まります。
\[ \begin{eqnarray} \left\{ \begin{array}{l} T_{fl} = D_{fl2} \ μ_{fl} \ \cfrac{F_{ax}}{2} \\ T_{thf} = \Bigl(\cfrac{D_2}{\cos⁡\alpha} \ μ_{th} + \cfrac{P}{\pi} \Bigr) \cfrac{F_{ax}}{2} \end{array} \right. \end{eqnarray} \] \[ \begin{eqnarray} \rightarrow T_{fl} & = & T_{fl} + T_{th} \\ & = & \Bigl( D_{fl2} \ μ_{fl} + \cfrac{D_2}{\cos⁡\alpha} μ_{th} + \cfrac{P}{\pi} \Bigr) \frac{F_{ax}}{2} \end{eqnarray} \] \[ \begin{eqnarray} \left( \begin{array}{lll} D \large{\text{：呼び径、}} & D_2 \large{\text{：有効径、}} & D_{fl2} \large{\text{：座面有効径}} \hspace{15pt} \\ P \large{\text{：ねじピッチ、}} & \alpha \large{\text{：ねじ山半角(30°)、}} \hspace{30pt} & F_{ax} \large{\text{：軸力}} \\ μ_{fl} \large{\text{：座面摩擦係数、}} & μ_{th} \large{\text{：ねじ面摩擦係数}} & \end{array} \right) \end{eqnarray} \]
（上式の力学的な導出については3章を参照ください。）
上式からわかるように、締付トルク\(T_f\)と軸力\(F_{ax} \ \)は比例関係にあります。 これをもとに、締付トルクと軸力の関係を簡易的に計算するのが次式になります。
\[ T_f = K_f F_{ax} D \large\text{[Nm]} \] \[ D \text{：ねじの呼び径}, \ K_f \text{：トルク係数と呼び、一般的に0.15～0.2} \]
簡易的に締付トルクと軸力の関係を計算するWebアプリ締付トルク（簡易版）と、より詳細に締付トルクと軸力の関係を計算するWebアプリ締付トルク（詳細版）を公開していますので、ご活用ください。

2．6．2．締付トルクの範囲

締付トルクは座面とねじ面の摩擦係数に依存します。 摩擦係数はばらつきがあるため、締付トルクもそれに合わせてばらつきます。 従って締付トルクは、摩擦係数のばらつきを考慮した上で必要な軸力を担保しなければなりません （他のパラメータもばらつき要因になりますが、摩擦係数による影響が最も大きい、と考えます）。
摩擦係数の上下限を\(μ_{low} \ \) 、\(μ_{up} \ \)として、締付トルクの範囲を決定する手順は次の通りです。
  1. 必要軸力\(F_{axo} \ \)から最小締付トルク\(T_{fmin} \ \)を決定する。
  2. 最小締付トルク\(T_{fmin} \ \)に対し、摩擦係数下限値\(μ_{low} \ \)での最小軸力\(F_{axmin} \ \)を算出する。
  3. 最小軸力\(F_{axmin} \ \)に対して摩擦係数上限値\(μ_{up} \ \)での締付トルク\(T_f'\)を算出する。
  4. \(T_f'\)に対して摩擦係数下限値\(μ_{low} \ \)での最大軸力\(F_{axmax} \ \)を算出する。
  5. 最大軸力\(F_{axmax} \ \)に対して摩擦係数上限値\(μ_{up} \ \)での最大締付トルク\(T_{fmax} \ \)を算出する。
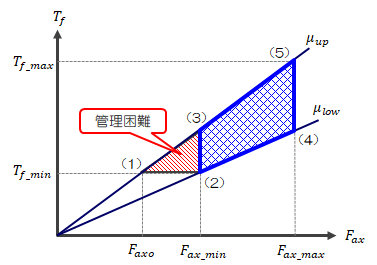
図2.6.2－1　締付トルク範囲
図2.6.2－1　締付トルク範囲
（1）～（5）のプロセスでは、締結体の強度を考慮していません。 実際は締付によっても締結体に応力が発生するため、ボルトが降伏しない軸力限界\(F_{axy} \ \)が存在します。 従って、
\[ F_{axy} < F_{axmax} \]
の場合は、最大軸力\(F_{axmax} \ \)を\(F_{axy} \ \)に置き換えなければなりません。

また本節の内容に基づいた締付トルク範囲計算をWebアプリページ 締付トルク（範囲）ページ で公開していますので、ご活用ください

2．6．3．標準ねじ締付トルク参考値

参考に、一般的なねじサイズでの締付トルクを記載しておきます。
表2.6.3－1　標準ねじ締付トルク参考値
ねじの
呼び径		 強度区分毎の締付トルク
8.8級 10.9級 12.9級
kgf·cm N·m kgf·cm N·m kgf·cm N·m
M3X0.5 10 1 15 1 17 2
M4X0.7 23 2 34 3 40 4
M5X0.8 47 5 69 7 81 8
M6X1 80 8 118 12 138 14
M8X1.25 195 19 286 28 334 33
M10X1.5 386 38 567 56 663 65
M12X1.75 674 66 990 97 1160 114
M14X2 1070 105 1580 155 1840 180
M16X2 1670 164 2460 241 2870 281
M18X2.5 2370 232 3380 331 3950 387
M20X2.5 3360 330 4790 470 5600 549
M22X2.5 4580 449 6520 639 7620 747
M24X3 5820 571 8290 813 9680 949

強度区分：JIS B 1051参照

参考文献

▲