gijyutsu-keisan.com

2．4．ばね定数の算出

2．4．1．締結体のばね定数

締結体に引張荷重\(W\)（被締結体を引き離す方向）が作用する場合を考えます。 ボルトは引張りばね、被締結体は圧縮ばねとみることができるので、ボルトのばね定数を\(K_{ex} \ \)、被締結体のばね定数を\(K_{bd} \ \)とします。 引張り荷重\(W\)の作用により、ボルトはさらに伸ばされ、軸力は\(F_{ax} \ \)→\(F_{B}\)に変化します。 また、被締結体の縮みは緩和され、圧縮力は\(F_{ax} \ \)→\(F_{C}\)に変化します。 すると、下図のようにボルトと被締結体はそれぞれ\(λ\)だけ伸びます。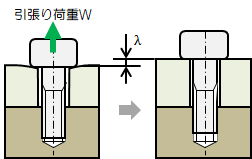
図2.4.1－1　引張り荷重
図2.4.1－1　引張り荷重
このとき、力の釣り合いから以下の式が導き出せ、\(F_{B}\)が求まります。
\[ \begin{eqnarray} \left \{ \begin{array}{l} F_B = W + F_C \\ F_B - F_{ax} = K_{ex} \lambda \\ F_C - F_{ax} = - K_{bd} \lambda \end{array} \right. \end{eqnarray} \rightarrow F_B = F_{ax} + \frac {K_{ex}} {( K_{ex} + K_{bd} )} W \tag{2.4.1-1} \]
これを図式化すると、次のようになります。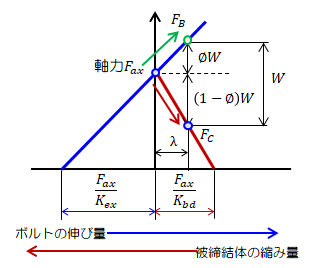
図2.4.1－2　外力作用時の締付線図
図2.4.1－2　外力作用時の締付線図
（2.4.1－1）式から、純粋に初期の軸力\(F_{ax} \ \)に外力\(W\)が足されるのではなく、外力\(W\)の
\[ \frac {K_{ex}} {( K_{ex} + K_{bd} )} = \phi 倍 (<1） \]
だけ足される、ということがわかります。 この倍数\( \phi \)を内外力比と呼びます。
この内外力比を踏まえた上でねじ計算をしないと、外力の引張り荷重に対して過剰な設計となってしまいます。

なお、本項で出てくる\(K_{ex} \ \)、\(K_{bd} \ \)は、材料の弾性係数と形状に依存します。 次節で示す簡易モデルを設定して手計算で求めるか、CAEによって求めることができます。

また本サイトではばね定数計算を、Webアプリページ ばね定数計算ページ で公開していますので、ご活用ください。

2．4．2．ボルトのばね定数

ボルトを下図のように各部位ごと（径が同じと考えられる範囲）に分割し、それぞれの部位を円筒ばねとみてばね定数を決定します。 最後にそれぞれのばねが直列につながっているものとして全体のばね定数\(K_{ex} \ \)を計算します。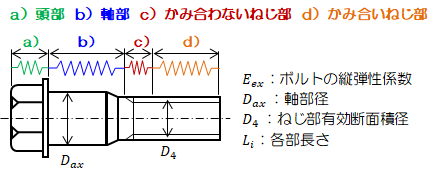
図2.4.2－1　ボルトのばね定数計算
図2.4.2－1　ボルトのばね定数計算
各部位のばね定数は次のように計算します。
\[ K_a = \frac {\pi D_{ax}^2 E_{ex}} {4 \times 0.6 D} \quad , \ K_b = \frac {\pi D_{ax}^2 E_{ex}} {4 L_b} \]
\[ K_c = \frac {\pi D_4^2 E_{ex}} {4 L_c} \quad , \ K_d = \frac {\pi D_4^2 E_{ex}} {4 \times 0.7 D} \]
これらを直列ばねとみて、ボルト全体のばね定数を算出します。
\[ \frac {1} {K_{ex}} = \displaystyle \sum_{ i = a,b,c,d }^{ n } \quad \frac {1} {K_i} \]

2．4．3．被締結体のばね定数

被締結体のばね定数\(K_{bd} \ \)は、その外径\(D_{bdo} \ \)と座面外径\(D_{fl} \ \)の関係により三通りに場合分けされます。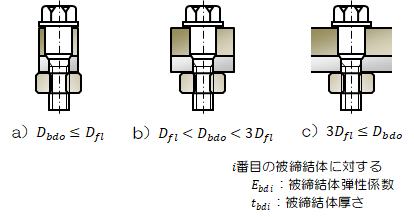
図2.4.3－1　被締結体のばね定数計算
図2.4.3－1　被締結体のばね定数計算
\[ \begin{eqnarray} &a) :& K_{bdi} = \frac {\pi E_{bdi}} {4 t_{bdi}} ( D_{bdo}^2 - D_{bdh}^2 ) \\ &b) :& K_{bdi} = \frac {\pi E_{bdi}} {4 t_{bdi}} \Biggl( (D_{fl} + \alpha_f k t_{bdi} )^2 - D_{bdh}^2 \Biggr) \\ & & k = \frac {1}{10} \Biggl\{ 1 - \frac{1}{4} \Biggl( 3 - \frac {D_{bdo}}{D_{fl}} \Biggr)^2 \Biggr\} \\ \\ &c) :& K_{bdi} = \frac {\pi E_{bdi}} {4 t_{bdi}} ( D_{bdo}^2 - D_{bdh}^2 ) \end{eqnarray} \]
この場合分けは、座面の押し付け力が効果を発揮する範囲を等価的に考慮した結果に基づいています。 また締結方法によって係数\(α_f\)が異なるのは、穴側の座面径の違いによるものです。 被締結体は複数の場合もあるため、各被締結体の厚さ、材質に合わせてそれぞれを計算し、直列ばねとして被締結体全体のばね定数を計算する必要があります。

2．5．軸力の算出

必要軸力をいくつに設定するか？は、締結ねじの設計上最も重要な検討項目となります。 軸力によって締結の能力が決まることは1.2節の説明の通りです。 締結において問題となる緩みにつながる事象が発生しないよう、軸力を設定しなければなりません。 この軸力設定で考えなければならない項目は以下の通りです。
  1. 被締結体の遊離（口開き）
  2. 被締結体のすべり
  3. 非回転緩みによる軸力変化量（座面のへたり、熱膨張差など）
それぞれに対する必要軸力の算出について見ていきます。

（1）被締結体の口開き（遊離）

締結体に引張り荷重\(F_t\)が作用するとき、その大きさによって下図のような締付線図が得られます。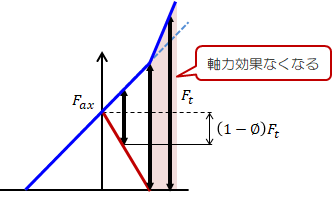
図2.5－1　被締結体遊離時の締付線図
図2.5－1　被締結体遊離時の締付線図
被締結体が口開きしないための条件は上図左から2本目の矢印線までで、被締結体の圧縮力が作用する範囲内となります。
\[ (1- \phi) F_t \lt F_{axt} \]
被締結体に口開きが生じないためには、この不等式が成立するような軸力に設定する必要があります。

（2）被締結体のすべり

締結体にせん断荷重\( F_s \)やねじり荷重\( M_{tor} \)が作用する場合に問題となります。 すべりが発生しないための条件は、軸力によって挟み込まれた被締結体が摩擦力によって動かないことであり、
\[ \begin{eqnarray} \frac {F_s}{μ} < F_{axs} （すべりの場合）\hspace{90pt} \\ \frac {2M_{tor}}{μD_{fl2}} < F_{axs} （ねじりの場合）( D_{fl2}：座面有効径) \end{eqnarray} \]
を満足することです。

(3) 非回転緩みによる軸力変化量

非回転緩みは、締結時に発生する面粗度のつぶれ等によるもの、使用温度環境に応じて材料の線膨張差によって発生するもの、座面陥没によるものなどが該当します。

非回転緩みによる軸力変化量の計算をWebアプリページ 軸力低下 ページで公開していますのでご活用ください。
（1）、（2）は締結体に作用する外力の影響が主であり、独立に起きたり、複合で起きたりとさまざまです。 使用条件に合わせて独立か、複合かを設定する必要があります。 （3）は使用上必ず発生する軸力変化量で、あらかじめ考慮しておく必要があります。
以上を考慮し、必要軸力\(F_{ax} \ \)は決まります（非回転緩みに対する必要軸力：\(F_{axres} \ \)）。
i）被締結体の口開きとすべりが独立に作用する場合
\[ F_{ax} > F_{axres}+Max(F_{axt},F_{axs} ) \]
ii）被締結体の口開きとすべりが同時に作用する場合
残存軸力がすべりを抑えられれば良いので、次のようになります。
\[ F_{ax} > F_{axres} + F_{axt} + Max(F_{axt} - (1-\phi) F_t,F_{axs} ) \]
軸力を大きくとりすぎると座面陥没、軸部破断やねじ山破壊などの破損につながります。 このように強度的な観点を考慮に入れて、適切な軸力範囲を設定する必要があります。

なお、必要最小軸力の計算をWebアプリページ 必要最小軸力 ページで公開していますので、ご活用ください。

参考文献

▲