1．物体の運動

1．1．運動の定義

力学における運動とは、「物体が時刻の変化とともに位置を変えること」です。 この運動の定義は、“空間”と“時間”という2つの基本概念^＊があって成立するものです。
さて、“空間”と“時間”はともに事物の存在範囲を示す概念であり、数学でいうところの集合を形成します。 特に空間は事物が存在する場所を示す点で構成され、時間は事物の変化を表す点（時点）で構成されます。 これらの点は、空間および時間に原点を設け、それとの位置関係によって区別され、 空間の点を位置、時間の点を時刻と呼びます。 またさらに、このように定義された位置の変化を変位、時刻の変化を時間といいます。

時間には2つの意味があり混同しそうですが、時刻も基準からの時間で定義される量のため、 時間の元も時間です。 そのため区別する必要なく扱えるはず、ということだと考えられます。

空間内の点の集合体には大きさと形が存在し、そこに何かしらの物理的性質が与えられたものを物体と呼びます。

図1.1－1　物体

以上で、運動を定義するための“物体”、“位置”、“時刻”、 それらの根本を形成する基本概念である“空間”、“時間”について言及しました。 ただし、空間と時間は非常に抽象的であり、明確な定義は今のところありませんし、その実態すらつかめていません。 そこで、空間と時間の理解を深めるには、様々な本に接するのが良いと思いますので、 ここでは次のような本を紹介しておきます。

1．2．座標系

位置や時刻を特定するには、距離と方向を決めるための“ものさし”が必要になります。 この“ものさし”は、点の位置を特定するのに必要となる数だけ設定します。 この数を次元と呼びます。 例えば、私たちが暮らす空間は（縦、横、高さ）の3つの値を決める“ものさし”が必要なため、三次元空間になります。 時間は1つの値で時刻を表せるので一次元になります。 このように、“ものさし”の組み合わせによって点を特定するシステムのことを座標系といい、 ものさしに相当するものを座標軸といいます。 また、各座標軸の値を順序づけた組（x,y,z）で表したものを座標といい、 各軸の値を成分と呼びます。

＊：順序組とは、（1,2）≠（2,1）のように順番が変わると異なる数値の組のことです。

座標は線形空間（線形代数を参照）の定義を満足すること、距離と方向という幾何学的な意味を持つことから、 位置ベクトルとも呼びます。 本サイトではベクトルを太文字、スカラーを普通字で表すことにします。
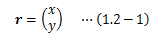なお、座標系は空間上に任意に設定可能で、その任意性により私たちは扱いやすい座標系を好きに設定してよいことになります。 ここで、力学で一般的に用いられる座標系と位置の表し方について見ていきます。
一次元の座標系は1本の数直線を座標軸とし、距離に正負の符号をつけて点を特定します。 二次元の座標系は2本の座標軸によって平面上の点を特定します。 その中で最も一般的なものは平面直交座標系（下図左側）で、 原点で直交する2本の軸（x,y軸）によって位置を特定します。 また、別の方法として平面極座標系（下図右側）があり、 原点からの距離rとx軸からの方位角θを成分とするものです。 なお、θの回転方向は、紙面から見て反時計回りを正とします。

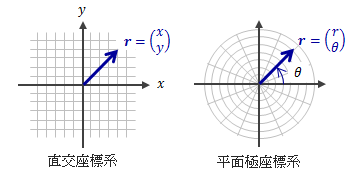
図1.2－1　二次元（平面）座標系

特に極座標については、位置ベクトルrの方向を動径方向、 このrを反時計回りに90度回転させたものを方位方向と呼びます。 そこで、各座標軸方向の単位ベクトルを次のように設定します。

図1.2－2　単位軸ベクトル

このとき位置ベクトルrは、軸方向単位ベクトルを用いて次のように表せます。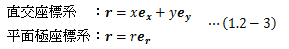
最後に三次元の主な座標系を列挙します。 三次元直交座標系は二次元直交座標系に直交するz軸を右手系に従う方向に追加したもので、 座標は（x,y,z）で表します。円柱座標系は、平面極座標系に同様のz軸を追加したもので、 座標は（R,θ,z）で表します。 極座標系は、動径rと2つの方位角θ、ψで座標（r,ψ,θ）を表したものです。

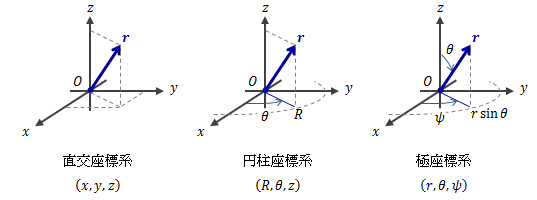
図1.2－3　三次元座標系

なお、極座標表現と直交座標表現の間には次式の関係があります。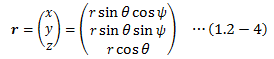

1．3．変位

1．3．1．変位の定義

変位とは「物体の移動に際し生じる元の位置からのずれ」のことで、 元の位置をr、移動後の位置をr’とすれば、変位uは次のように表せます。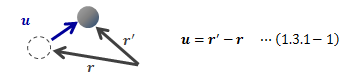

図1.3.1－1　変位

なお、力学では無限小（微小）変位が興味の対象となることから、以降では無限小変位について見ることにします。

1．3．2．回転変位

二次元の無限小変位drを極座標系で表すと、次のようになります。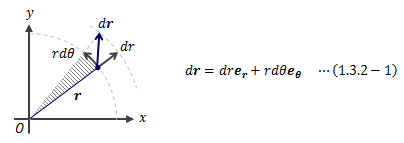

図1.3.2－1　平面極座標による変位

方位成分rdθは原点Oまわりの回転によって得られる変位であり、これを回転変位と呼びます。 特に無限小変位の場合、回転変位は直線近似できます。 さて回転変位は、位置ベクトルrを掃引することによって扇形の平面を張ります（上図斜線部）。 つまり回転変位が存在する条件は、この扇形の面積が0でなければよい、 もっと簡単に言えば空間的な広がりが生じればよいことになります。 ただし注意点として、直線運動でも回転変位が生じる場合があります。 それは、rとdrが原点Oを通る1つの直線上に乗らない場合、 時々刻々とe_rの向きが変わるためです。
次に、三次元に話を拡張します。 三次元における無限小変位drの極座標表現は次のようになります。

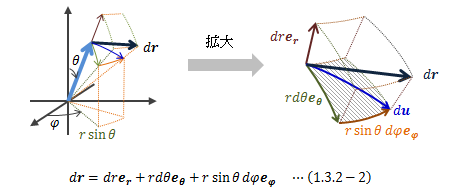
図1.3.2－2　三次元極座標での無限小変位

ただし、各軸方向の単位ベクトルは次の通りです。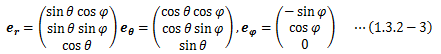
この内容からわかることは、次の通りです。 （1.3.2－2）式の第二項と第三項の和をduとします。 このduは半径rの球面上の変位であるから、duもまた原点Oまわりの回転変位になります。 そこで、ある無限小回転角をdεととれば、（1.3.2－2）式は平面極座標と同じ形で表すことができます。
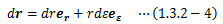このように、三次元における無限小変位の回転成分は、原点を通る1つの軸まわりの回転で表すことができます。
さて、無限小回転変位の存在は、前述のように位置ベクトルrの掃引によって得られる面の面積dSを求めればよく、 それは位置ベクトルrと無限小変位drの外積の絶対値によって求められます。
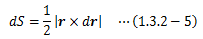さらに、この面積をベクトルとして以下のように定義したとき、
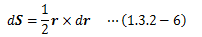このベクトルの向きはr、dr、dSの順に右手系を成す方向になります。

1．3．3．回転ベクトル

ここでは、複数の軸まわりの無限小回転変位について考えます。 1つ目の軸まわりの無限小回転角dεで得られる変位の大きさduは次式で表せます。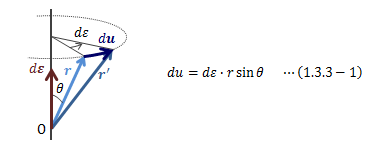

図1.3.3－1　回転変位

このとき、右ねじの法則に従う回転軸方向にdεの大きさを持つ無限小回転ベクトルdεを定義します（上図の赤矢印線）。 すると回転変位duはdεとrの外積によって得られます。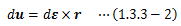
したがって、回転によって得られる新たな位置ベクトルr’は次式で表せます。
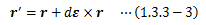同様に、このr’を別の軸まわりに無限小回転角dε’で回転させれば、 新たな位置ベクトルr’’は二次以上の微小項を無視して次のように表せます。
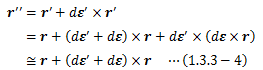ところで、回転変位がベクトルの外積によって定義できるのであれば、 複数の軸まわりの回転変位はそれぞれの軸の回転ベクトルの和（dε’＋dε）の外積によって定義できるはずです。 （1.3.3－4）式はこの条件を満たしていますが、回転角が無限小（二次以上の項が無視可能な微小角） であることが制約としてついています。 もし回転角が無限小でなければ、少なくとも（1.3.3－4）式導出過程の三重積が残り、 回転ベクトルの和は回転変換に対し交換則を満足しません。 そのため、ベクトルに要求される線形空間の定義を満たせなくなるため、 無限小でない回転ベクトルはベクトルではないことになります。 以上から、無限小回転の概念によってはじめて回転ベクトルが定義されることになります。
この無限小回転の概念に関する詳細は、こちらの書籍に詳しく掲載されています。

1．4．速度

1．4．1．速度の定義

物体の運動は時間とともに変位を生じることですから、単位時間あたりの変位によって運動の勢いを表すことができます。 これを速度といいます。 特に無限小変位に対する速度、つまり位置rの時間微分によって速度を定めれば、 その位置での瞬時速度が求まります。 一般にはこの瞬時速度を速度として扱い、有限な変位に対する速度を平均速度として扱います。 なお、速度の大きさ|v|＝vを速さといいます。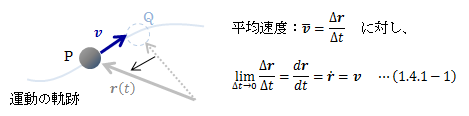

図1.4.1－1　速度

速度は、その定義からわかるように運動の軌跡に接するのが特徴です。 また、速度を時間で積分すると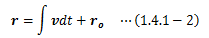
が得られ、初期値を設定することで、運動の軌跡を特定することができます。 この特定によって、物体の位置があらゆる時刻で予測可能となり、 力学的状態の決定とはまさにこのことを指します。 特に速度vが一定の場合、（1.4.1－2）式は非常に簡単になります。
これは、時間とともに速度方向に直線的に移動する運動であり、等速度運動といいます。 それに対し、速さvが一定の運動を等速運動といいます。 等速運動は速さが一定で運動の方向が変わる運動、例えば円運動も含まれます。

1．4．2．角速度

速度を、直交座標系と極座標系で成分表示すると次のようになります。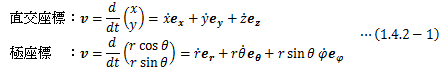
当然ですが、これらは微小変位を微小時間dtで割ったものと一致します。 ところで、極座標表現については1.3節で見たように、 その瞬間において1本の軸周りの平面回転運動として扱うことができるので、方位角をεとおいて
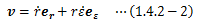と書き直すことができます。 このとき、速度の方位成分には角度の時間微分が現れます。 これを角速度といい、ある基準点周りの回転の勢いを表すものであり、 また運動の方向変化の勢いを表すものです。
この角速度は瞬時の回転変位に対して定義されていることから、無限小回転の概念 （1.3.3節）が適用できます。 そこで、無限小回転ベクトルdθを微小時間で割ったもの、 つまり方位角の時間微分を角速度ベクトルωと定義します（図1.3.3－1参照）。
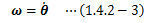すると速度の方位成分は、回転変位（1.3.3－2）式を微小時間で割って得られることから
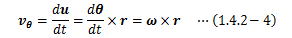になり、速度の極座標表現は次のように書き直すことができます。
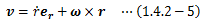さて、回転変位の存在はrの掃引によって得られる面の面積ベクトルdS（1.3.2－6）式を 微小時間で割れば単位時間あたりの面積変化を表すことができます。 これを面積速度と呼びます。
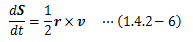1.3.2節の話から、この面積速度を求めることで、回転変位の存在を知ることができます。

1．5．モーメントの概念

1.3、1.4節において、回転運動がベクトルの外積と強く結びついていることがわかりました。 そこで本節では、回転に関する基本概念であるモーメントについて見ることにします。 ただし、ここでは力学に限らない一般的なモーメントの概念から入ることにします。
空間内の原点Oから距離rの位置に、何らかの量aが生じているとします。 このrとaに直交関係^＊があるとき、 rとaの積によって定まる量をモーメントといいます。

＊：ここでは幾何学的な直交以外にも、“変数として独立”の意味も含めます。

モーメントとは距離に何らかの量の重みづけを与えたもので、基準点から遠ければ遠いほど、 あるいは重みづけ量が大きければ大きいほど、モーメントは大きくなります。 このような考え方が重要となるものに、統計学における平均や分散などが挙げられます。
次に、幾何学的観点からモーメントを捉えれば、位置ｒとその点に生じる何らかのベクトルAの外積が、 基準点まわりのモーメントベクトルMになります。 その理由は次の通りです。

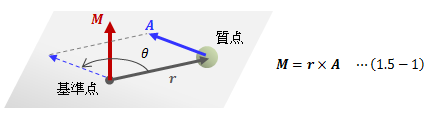
図1.5－1　モーメントの定義

モーメントベクトルMの大きさは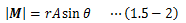
であり、この式はAの、rに対して垂直な成分を掛け合わしたものを表します。 よって、ベクトルの外積による定義はモーメントの一般定義に合致します。 1.3.2節の回転変位でも見たようように、 この位置ベクトルrとある物理ベクトルAが張る面の面積が0でなければ、 モーメントMによって空間的な広がりが生まれることがわかります。 つまり、モーメントは回転運動と強く結びついていると考えることができます。

参考文献

関連ページ