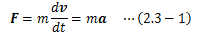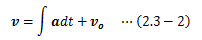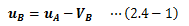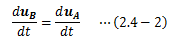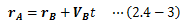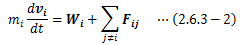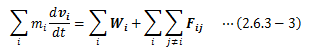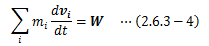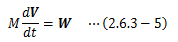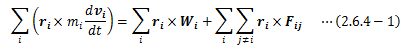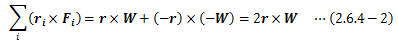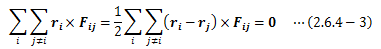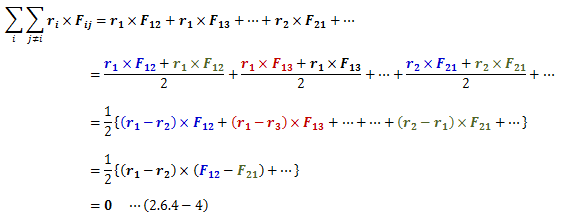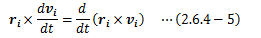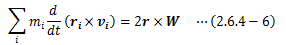運動の法則
2.1.ニュートンの運動の法則
私たちにとって“力”は当たり前の存在ですが、その正体は残念ながら不明です。 そのため、今の科学では“力”の存在を無条件に肯定し、 力と運動の間にある法則を明らかにする方法をとっています。 この力と物体の運動との間にある法則を、ニュートンは3つにまとめました。第一法則:慣性の法則
物体は力の作用を受けない限り、静止または一直線上の一様運動を続ける*慣性:現状の運動を維持しようとする性質
第二法則:運動の法則
物体の運動の変化は、その物体に働く力に比例し、力の働く向きに生じる第三法則:作用・反作用の法則
物体1が物体2に力を及ぼすとき、物体2は物体1に対して同じ大きさで逆向きの力を及ぼす力学はこの3つの法則を公理として構築されており、 これらをあわせてニュートンの運動の法則といいます。 この法則の経緯については、様々な本で紹介されていますが、 ここではその一部を紹介しておきます。
2.2.慣性系
慣性の法則(第一法則)は、力の作用がない限り物体の運動に変化は生じないことを宣言しています。 これは空間と時間に対し、次の性質を暗に要求しています。- 空間の一様性と等方性
- 時間の一様性と等方性
空間の一様性と等方性は、位置や方向によって空間の性質は変わらないことを意味しています。例えば、ボールの中に入ってボールの内面を走り回る状況が当てはまります (ゴルフボールのように凹凸があったりラグビーボールのように曲率の違うところがあるものはだめです)。 時間の一様性と等方性は、時刻や過去~未来によって時間の性質は変わらないことを意味しています。 つまり、物体の運動は空間や時間によって変化するのではなく、あくまで“力”によってのみ起こる、 という制限を設けていることになります。 このような空間と時間の性質を保持する座標系を慣性系といいます。 慣性系は運動の法則(第二法則)の前提条件となる非常に重要な概念です。 もし空間や時間にこれらの性質がなければ、 物体に力が作用しなくても勝手にその運動を変えることになり、 運動の法則(第二法則)に反するためです。 なお、この概念を基本に力学を展開する本を以下に紹介します。
2.3.運動方程式
1.4節で見たように、速度によって物体の運動を表すことができます。 そのため、運動の変化とは速度の時間変化を含みます。 運動の法則(第二法則)では、この速度の時間変化と力が比例することを宣言しています。 そこで、比例定数をmととれば運動の法則は次のように数式化できます。この式を運動方程式と呼び、比例定数mを質量、速度の時間微分aを加速度といいます。 質量とは、物体それぞれの動かし難さ、つまり物体固有の慣性を定量化したスカラー量であることが経験的にわかっています。 質量はスカラーゆえ空間や時間に対して不変です。
*:重量と質量の違いについては別途話をします。 なお、質量についても力同様未解明なものであり、その詳細については下記に譲るものとします。
さて、加速度を積分することで速度を特定でき、(1.4.1-2)式によって最終的には運動の軌跡を特定することができます。
運動方程式によって加速度が決まることで、最終的には物体の運動の軌跡が特定されます。 つまり、運動方程式の本質的な意味は、加速度を座標および速度と結びつけることで、 力学的状態を決定することにあります。
最後に、運動方程式から得られるいくつかの見解について触れておきます。
まず、運動方程式は力の定義式ではなく、加速度と力が等価であることを意味しているだけです。 力が作用すれば加速度は生じ、加速度が生じれば力が作用する、どちらが先、というものではありません。
二点目として、力がベクトルであることに由来して、力には独立性があります。 1つの物体に2つ以上の力が同時に働く場合、それらはベクトル的に重ね合わさるだけで、 元の力が影響し合って別の力に変化することはありません。
三点目は、力Fが物体の位置のみで定まるとき、時刻toで速度を向きだけ反転させると、 任意のtに対し、時刻to+tとto-tで同じ位置を通過します。 これは、加速度が時間で2回割って決まることから直ちに理解できます。 このような運動の特性を可逆性と呼びます。 この可逆性は時間の方向性に依存しないことを意味しており、時間の等方性に起因する性質になります。 この運動の可逆性は熱力学において重要な概念となります。
2.4.ガリレイの相対性原理
慣性系が無数に存在することを証明します。 慣性系Aと、Aに対して任意の一定速度VBで運動する座標系Bを設定します。 Aから見た物体の速度uAをBから見ると次式で表せます。この式の両辺を時間tで微分すれば、物体の加速度はA、Bとも同じになります。
さらに、質量は座標系に対し不変なため、運動方程式はA、B全く同じになります。 つまり座標系Bもまた慣性系となります。 また、速度VBは任意ゆえ無数の慣性系が存在し、以上で証明は完了です。 このように、任意の慣性系が力学的に完全に同等であることをガリレイの相対性原理と呼びます。 この原理において、2つの慣性系A、Bから見た質点の位置をrA、rBとすると、
の関係式が成り立ちます。 このときの前提として、時間の進み方は2つの慣性系で同じであることが暗に仮定されています。 このように、任意の座標系に対して時間の進み方が不変となる概念を絶対時間と呼びます。 この概念はニュートン力学における前提条件になっていますが、アインシュタインの相対論と矛盾します。しかしながら、私たちの身近な運動において、絶対時間の概念を取り入れても問題はありません (唯一身近なところといえば、人工衛星の時間補正ぐらいでしょうか)。
2.5.相互作用
現時点で力とは何か?について知ることはできませんが、 どんな力があるか?については知られている範囲で答えられます。 現在、基本的な力として考えられているのは、次の4つです。- 万有引力
- 質量を持つものの間に働く引力
- 電磁気力
- 電荷を持つものの間に働く引力/斥力
- 弱い核力
- 原子核や素粒子の間に働く力*
- 強い核力
*:実際の分類は(1)、(2)と(3)、(4)という形で、 (3)(4)をひとくくりにはしないようです。
世の中にある物質や系は、これらの力によって構成され、形作られています。 ところで、これら4つの力に共通しているのは“~の間に働く”ということです。 つまり1つのものだけでは力は働かない、ということを示唆しており、 複数の物体の間に働く相互作用が力の源になっている、と考えることができます。 この相互作用による力の発生が物体の接触を必要としないことは、 上記4つの力から言えます (むしろ接触という現象自体が人間の感覚的で、 ミクロで見れば接触もまた結局は非接触な力によるものです)。 さらに、相互作用による力は、作用・反作用の法則(第三法則)によって両物体に同じ大きさで互いに逆向きに働きます。 このときニュートン力学では、力の伝達が一瞬で行われることを前提としており、 これを遠隔作用の力と呼びます。これは絶対時間 (2.4節)によって得られる概念です。 実際、力の伝達は有限の速さで行われるのですが、 私たちの身近な現象において力を遠隔作用として扱っても特に問題はありません。 ちなみに、有限の速さで伝達される力を近接作用の力と呼びます。
2.6.質点の概念
2.6.1.並進と回転
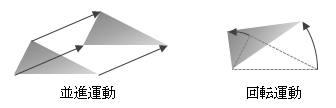
物体は、以下に示す2つの運動の複合形態をとるのが一般的です。- 並進運動
- 物体は向きを変えず、平行に移動する運動
- 回転運動
- 物体はその内部の基準点まわりに向きだけを変える運動
図2.6.1-1 並進運動と回転運動
この定義に従えば、惑星の運動における公転は並進運動、自転は回転運動に該当します。 公転と自転の明確な違いは、公転では惑星の大きさを考慮しなくてよいのに対し、 自転はその大きさを考慮する必要がある、ということと、 回転の基準点が公転では惑星の外部に、自転ではその内部にある、という2点です。
2.6.2.質点の概念
質点とは、その大きさや形状を考慮せず1つの点として扱う概念です。 物体を質点として扱うか否かは考察対象とする運動の条件によって異なり、 前節のような回転(自転)や変形を考慮しない場合に適用します。 それに対し、複数の質点の集合体を質点系と呼びます。 物体を細かな領域に分割すれば、その各々を質点とみなすことができるため、 物体を質点系として扱うこともできます。 質点の運動として表せない場合、物体を質点系として扱うことで運動を表現できます。図2.6.2-1 質点の概念
なお、ニュートンの運動の三法則は質点に対する法則であって、 回転運動に対してはそのままの形で適用できません。 ただしほんの少しの工夫を施せば、回転運動もニュートンの運動の法則に従います。 この点については2.6.4節でその詳細を見ることにします。
2.6.3.質点系の運動方程式
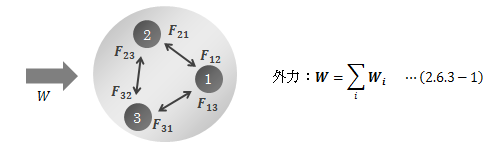
今、質点系の外から作用する力(外力)をWとし、 系内部の質点間相互作用をFijで表しします。図2.6.3-1 質点系内の質点の運動
このとき、系内の1つの質点について運動方程式を書くと次のようになります。
これを系内のすべての質点に対して足し合わせると、
となりますが、作用・反作用の法則(第三法則)によりFij=-Fjiであり、 内力の合計は“0”となります。 そのため、最終的に質点系の運動方程式は次式になります。
もし質点系が一つの物体で変形も回転もしない場合、すべての質点の速度は同じになるため、 物体の質量をM、質点の速度をVと表せば、質点の運動方程式と全く同じ形になります。
さて、外部からなんら影響を受けない系を孤立系と呼びます。 孤立系は外力の作用は受けませんが、内力の作用は考慮します。
2.6.4.回転運動に対する問題
下図のように変形しない一様な棒の両端に、同じ大きさで反対向きの力Wを与えます (平面内の運動を仮定します)。図2.6.4-1 力の与え方による違い
棒を質点とすれば、運動方程式(2.3-1)式からどちらのケースも運動を行わないはずです。 しかしながら、ケース2は棒の中心Oを基準に回転し、ケース1の状態になって静止します。 これは力の作用線が、ケース1では一致しているのに対し、ケース2では一致していないためです。 つまり、回転運動は力が作用する位置と方向に依存します。 よって、棒を質点として扱えないことがわかります。 さらに棒を質点系として捉えたとしても、系に加わる外力が0であることは変わらず、 (2.6.3-4)式から結局は回転運動を運動方程式によって表すことはできません。以上の結果から、回転運動を表すには新たな概念の導入が必要になります。 そこで、 1.5節 で見たモーメントの概念を質点系の運動方程式(2.6.3-3)式に適用します
ただし、外力は棒の両端のみに作用しているので、右辺の力のモーメントは
となります。 さらに、(2.6.4-1)式右辺第二項である内力の項は、 作用反作用の法則(第三法則)を用いることで0となり、 運動方程式のとき同様内力の影響は受けません。
具体的な計算は以下の通りです。
また、左辺については
の関係があることから、(2.6.4-1)式は次のように書き換えられます。
この式から、各質点の位置ベクトルと速度ベクトルの外積が0でなければ棒は回転運動を行うことになり、 また逆に力のモーメント(位置ベクトルと外力の外積)が0でなければ棒は回転運動を行うことになります。