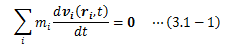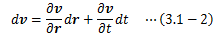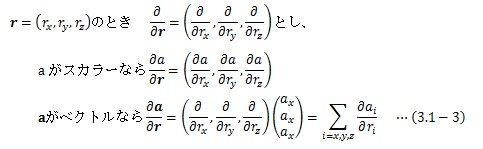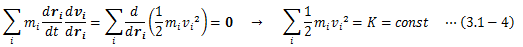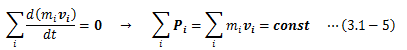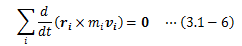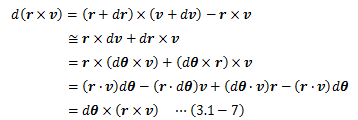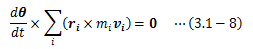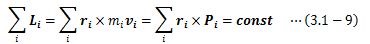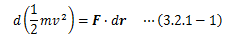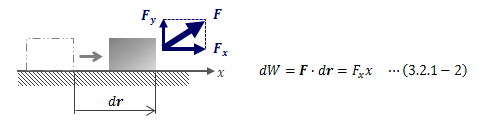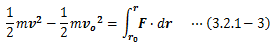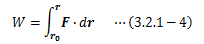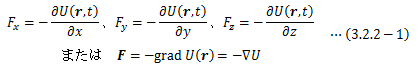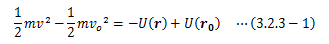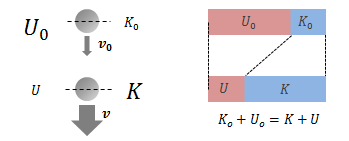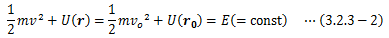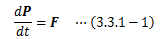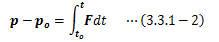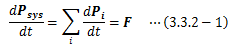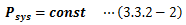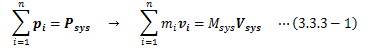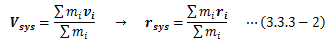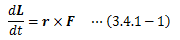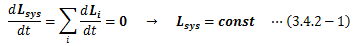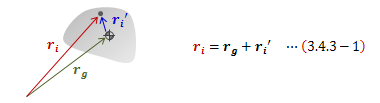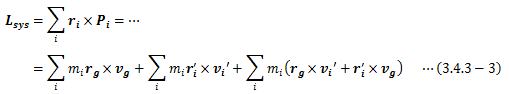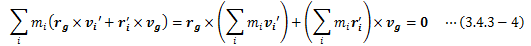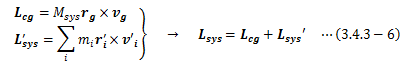力学

3．運動の積分形と保存則

3．1．保存量に必要な概念

今、外部とのやり取りを一切行わない質点系について考えます。このような系を孤立系と呼び、力学的には質量が不変かつ外力が作用しない系のことを言います。このとき、孤立系の運動は慣性の法則（第一法則）に従い不変となり、運動のあいだ一定に保たれる量が存在します。この保存量は運動の初期条件から決まり、このような関数を運動の積分といいます。積分とつく理由は、運動方程式の積分から得られる関数、という意味合いが含まれるためです。
ここで、空間と時間の基本性質に基づく保存量の導出を、孤立系に対して行います。孤立系の運動方程式は次のようになります。

また、速度の完全微分形は以下で表せます。

なお、ベクトルによる微分は次の演算に従うことにします。

（1）時間の一様性に基づく保存量

時間の一様性によって、孤立系は時間変化のみでその運動を変えません。つまり、速度はtを陽に含みません。よって速度の完全微分形（3.1－2）式から右辺第二項を落とせるので、運動方程式は以下に示す保存量K（スカラー）を導き出せます。

このKを運動エネルギーと呼びます。運動エネルギーの詳細については 3.2節で見ることにします。

（2）空間の一様性に基づく保存量

空間の一様性によって、孤立系は位置変化のみでその運動を変えません。つまり、速度はrを陽に含みません。よって速度の完全微分形（3.1－2）式から右辺第一項を落とせるので、運動方程式は以下に示す保存量P（ベクトル）を導き出せます。

このPを運動量と呼びます。運動量の詳細については 3.3節で見ることにします。

（3）空間の等方性に基づく保存量

空間の等方性によって、孤立系は空間内のある1点を基準にした任意の回転移動によってその運動を変えません。この場合、系内の各点に与えられる回転変位の回転角はすべて共通です。ところで、回転については運動方程式そのものでは表現できず、運動方程式のモーメントをとった（2.6.4－6）式で表します（2.6.4節参照）。

このとき

が得られ、（3.1－6）式はとなります。

今、任意の回転移動に対して運動を変えないという条件から、（3.1－8）式はdθに対する恒等式である必要があります。よって、以下に示す保存量L（ベクトル）を導出することができます。

このLを角運動量と呼びます。角運動量の詳細については 3.4節で見ることにします。

以上が、空間と時間の基本性質に深く結びついた保存量となります。孤立系においてはこれらすべての運動の積分が保存量となります。しかしながら非孤立系においては、ある条件下にあった形で運動の積分が保存量となります。

3．2．エネルギー保存則

3．2．1．仕事とエネルギー

3.1節（1）では、時間の一様性に基づく孤立系の保存量＝運動エネルギーを導出しました。ここでは非孤立系に対して話を拡張します。なお、ここでは話を簡単にするため、質点系を質点として扱います。
孤立系では運動エネルギーが一定となりますが、非孤立系の場合外力を受けるので、運動エネルギーは変化します。このとき（3.1－4）式は次のように書き換えられます。

この式によって、運動エネルギーの変化に寄与するのは、ベクトルの内積の定義から変位方向と一致する外力成分のみであることがわかります。この“力と微小変位の内積”を（微小）仕事と呼びdWで表します。

図3.2.1－1　質点の移動に関与する力の成分（例）

（3.2.1－1）式は、質点の移動経路に沿ってr_oからrの範囲で積分でき、

となります。この式の左辺は、質点の移動に伴う運動エネルギーの変化量を表し、右辺は質点の移動に寄与した力成分と距離の積を表します。特に右辺を仕事と呼びます。

上式から仕事は物体の移動経路に依存します。最短で移動すれば仕事は少なく、寄り道をすれば仕事が増えるのは私たちの行う仕事とまったく同じです。
さて、ここでエネルギーの意味について考えてみます。質点の速さをv_oからvにするには、外からの仕事Wが必要になります。これを逆から見れば、質点が外へ仕事Wを行えば、その速さはvからv_oになることを意味します。このように、質点は速さに従う仕事を行う能力を持つことになります。つまり、エネルギーとは「仕事をする能力」を意味し、質点に与えられた仕事はエネルギーとして蓄えることができます。
さて、現実にはこのエネルギーをすべて仕事に変換できるわけではありません。これは熱力学の問題になりますが、エネルギーは熱によって放出される仕事として使えない無効エネルギーと、仕事に使える有効エネルギーの2つに分かれるためです。この詳細については、熱力学のページで見ることにします。

3．2．2．保存力

物体の相互作用によって得られるスカラー関数U(r,t)について、その座標の導関数が力となるものをポテンシャルと呼びます。

特にポテンシャルが時間tを含まず位置rの一価関数^＊U(r)である場合、そこから得られる力を保存力と呼びます。保存力の呼び名は、後で出てくる力学的エネルギー保存則を満足する力ということから付いています。

図3.2.2－1　一価関数

この保存力の行う仕事は

であり、経路に依存せず始点と終点の位置のみで決まります。さらに言えば、質点に蓄えられるエネルギーは、その位置によって決まることからU（r）を位置エネルギーと呼びます。位置エネルギーもまた時間tを陽に含まないことから、時間の一様性の条件を満足しています。

3．2．3．エネルギー保存則

エネルギー方程式（3.2.1－3）式の仕事に、保存力の仕事（3.2.2－2）式を代入します。

これは、質点が位置r₀からrに移動した際の運動エネルギーの増加量と位置エネルギーの減少量が等しく、さらに位置エネルギーが運動エネルギーに変換されたことを意味しています。

図3.2.4－1　運動エネルギーと位置エネルギーの関係

（3.2.3－1）式について初期条件を右辺にまとめて書き直せば、

となり、質点に保存力のみが作用する場合、運動エネルギーと位置エネルギーの和は時間に関係なく常に一定に保たれることになります。これを力学的エネルギー保存則と言います。このように、力学的エネルギー保存則は時間の一様性と深く結びついています。

3．3．運動量保存則

3．3．1．運動量と力積

3.1節（2）では、空間の一様性に基づく孤立系の保存量＝運動量を導出しました。ここでは、非孤立系に対して話を拡張します。
質点の運動量Pは、（3.1－5）式によって質量mと速度vの積で定義されており、これを運動方程式に当てはめれば次のように表すことができます。

この式から運動の法則（第二法則）は、「運動量の時間変化と力は等しい」、と言い換えることができます。次に、運動方程式（3.3.1－1）式を時間toからtの間で積分するとき、

この式の右辺を力積と呼び、力積と運動量の時間変化は等しいことを表しています。

3．3．2．運動量保存則

質点系全体の運動は内力に影響されず、外力のみで決まることは 2.6.3節で見たとおりです。そこで、系全体の運動量Psys、各質点の運動量Piとして、質点系の運動方程式（2.6.3－4）式は次のように書き換えられます。

この式から結局は3.1節（2）で見たとおり、質点系に外力が作用しなければ系全体の運動量は一定となり、 運動量保存則が成り立ちます。

質点系の運動量が保存される場合、系内の質点が乱雑に運動していたとしても、外力が作用しない限り系全体の運動に変化は生じません。
なお、運動量保存則はベクトル式であることから、各軸ごとに独立に運動量保存則が成立します。例えば、x軸のみ運動量が保存し、y、z軸方向は運動量が保存されない、といったようなケースも存在します（ボールの壁あてなど）。