締結ねじ設計
3.ねじの力学
ねじの締付トルク\( T_f \ \)は、座面摩擦トルク\( T_{fl} \ \)とねじ面摩擦トルク\( T_{th} \ \)の合計で定まります。\[
T_f = T_{fl} + T_{th}
\]
座面摩擦トルク\( T_{fl} \ \)は軸力\( F_{ax} \ \)と座面\( \mu_{fl} \ \)の積から簡単に求まりますが、ねじ面摩擦トルク\( T_{th} \ \)については少々厄介な計算が必要です。ここでは、ねじ面摩擦トルク\(T_{th} \ \)を決定付けるねじ面接線力\(F_{th} \ \)を、ねじ面の力学的関係から定めるところについて焦点をあてていきます。
まずは、ねじ面の展開図を考えます。
ねじ面上の微小領域Pに作用する軸力、垂直抗力、摩擦力、ねじ面接線力をそれぞれ\(dF_{ax} 、dR_{th} 、df_{{\mu}th} 、dF_{th} \ \)とするとき、次の積分が成り立ちます。
\[
F_i = \oint dF_i \quad (i=ax,th,{\mu} th)
\]
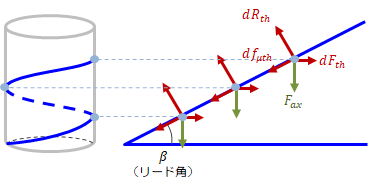
図3-1 ねじ面の展開図
この展開図からねじ面に作用する力は、ねじの回転に対して常に同一方向であることがわかります。次に、ねじ面上の任意の微小領域Pに着目します。
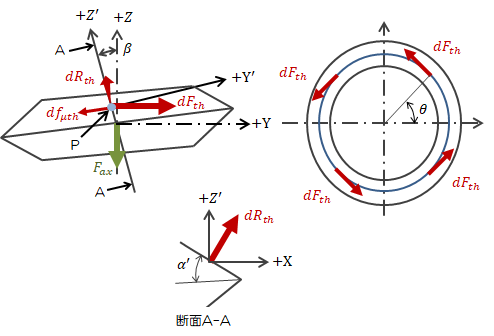
図3-2 ねじ面の力線
まずは、微小領域Pの単位法線ベクトルを求めるため、上図のように2つの座標系XYZ、XY’Z’をとります。 ただし、微小領域Pの位置に追従してX軸、Y軸、Y’軸は動くものとします(角度\( \theta \)に依存)。 まずは座標系XY’Z’から見た場合のねじ面法線ベクトルは、\[
n'_a = \left(
\begin{array}{c}
\sin { \alpha' } \\
0 \\
\cos { \alpha' }
\end{array}
\right)
\]
となります。
これをXYZ座標系から見るには、X軸まわりに\( \beta \)だけ回転させればよく、\[
n_a = \begin{eqnarray}
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos { \beta } & -\sin { \beta } \\
0 & \sin { \beta } & \cos { \beta }
\end{array}
\right)
\end{eqnarray}
\left(
\begin{array}{c}
\sin { \alpha' } \\
0 \\
\cos { \alpha' }
\end{array}
\right)
=
\left(
\begin{array}{c}
\sin { \alpha' } \\
-\sin { \beta } \cos { \alpha' } \ \\
\cos { \beta } \cos { \alpha' }
\end{array}
\right)
\]
となります。図3-1で見たように、ねじ面に発生している力は同じ方向を向いています。 これは、つる巻状に巻きつければ180度反対の位置の力は円柱断面に対してすべて反対向きになることを意味します (図3-2の円柱断面を参照)。 そのため、ねじ面の動径方向(中心に向かう方向)の力は打ち消し合い、最終的には径の接線方向と軸方向(z軸)のみとなります。
以上から、軸方向の力と径の接線方向のつり合いは次のようになり、
\[
\begin{eqnarray} \left\{
\begin{array}{l}
F_{ax} = R_{th} \cos { \alpha' } \cos { \beta } - f_{\mu {th}} \sin { \beta } \hspace{15pt} \\
F_{th} = R_{th} \cos { \alpha' } \sin { \beta } + f_{\mu {th}} \cos { \beta } \hspace{15pt} \\
f_{{\mu}th} \cos { \beta } = \mu_{th} R_{th}
\end{array}
\right.\end{eqnarray}
\]
軸力\( F_{ax} \)とねじ面接線力\( F_{th} \)の関係が明らかになります。\[
F_{th} =
\frac{ \cos { \alpha' } \sin { \beta } + \mu_{th} \cos { \beta } \hspace{ 15pt } }
{ \cos { \alpha' } \cos { \beta } - \mu_{th} \sin { \beta } \hspace{ 15pt }} F_{ax}
\tag{ 3-1 }
\]
次に、角度\( \alpha \)(ねじ山半角)、\( \alpha ' \)、\( \beta \)(リード角)の関係について調べます。\[
\tan \alpha ' = \frac {\sin \alpha \cos \beta}{\cos \alpha}
= \tan \beta \cos \beta
\tag{ 3-2 }
\]
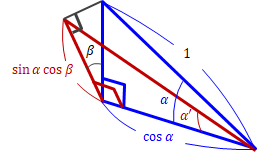
図3-3 角度の関係
リード角\( \beta \)については、ねじピッチP、呼び径Dを用いて次のように表せます。\[
\beta = \frac { P } { \pi D }
\]
ここで仮にM6の標準ねじの場合で計算してみると、\( \beta \)=0.05[rad]になり、2\( \pi \)(1回転)に対して十分小さいと言えます。
よって、(3-2)式は近似的に扱え、\( \alpha \)≒\( \alpha ' \)とすることができます。
そこで、この関係を(3-1)式に代入すると、\[
F_{th} =
\frac{ \cos { \alpha' } \sin { \beta } + \mu_{th} \cos { \beta } \hspace{ 15pt } }
{ \cos { \alpha' } \cos { \beta } - \mu_{th} \sin { \beta } \hspace{ 15pt }}
F_{ax} \fallingdotseq
\frac { \tan { \beta } + \cfrac { \mu_{th} } { \cos { \alpha } } \hspace{ 15pt } }
{ 1 - \cfrac { \mu_{th} } { \cos { \alpha } } \tan { \beta } \hspace{ 15pt } } F_{ax}
\tag{ 3-3 }
\]
となります。
実用的な範囲を考える場合\( \alpha \)=30°、\( \tan\beta \)≒0.05、\( \mu_{th} \ \)は大きくても0.5程度とみれば、分母は\[
1 - \frac { \mu_{th} } { \cos { \alpha } } \tan { \beta }
\fallingdotseq 1 - \frac { 0.5 \times 0.05 } { \sqrt { 3 } }
\fallingdotseq 1
\]
とできるので、\[
F_{th}
\fallingdotseq
\Bigl( \tan { \beta } + \frac { \mu_{th} } { \cos { \alpha } } \ \Bigr) F_{ax}
\tag { 3-4 }
\]
となります。
このねじ面接線力と軸力の関係が決まることで、締付トルクの設定計算ができるようになります。


