締結ねじ設計
2.7.強度検討
2.7.1.軸部の締付応力
ボルトを締めすぎると、ボルトの軸部をねじり切ってしまう場合があります。 これは締付時にはボルトの軸部に、軸力による引張り応力\(\sigma_{tf} \ \)とねじりによるせん断応力\(\tau_{tf} \ \)が同時に発生するためです。 このときボルトの降伏をミーゼスの降伏条件によって評価します。 これは、引張り応力\(\sigma_{tf} \ \)とせん断応力\(\tau_{tf} \ \)からなる次式で示す等価応力\(\sigma_{eq} \ \)が、材料の引張り降伏\(\sigma_y\)よりも小さければボルトは降伏しない、とする評価方法です。\[
\sigma_{eq}
=
\sqrt{ \sigma_{tf}^2+C_{eq} \tau_{tf}^2 } < σ_y
\]
\[
( C_{eq} \large{\text{:等価応力係数。一般に}} \normalsize{3か1.8} )
\]
これを図式化すると下図のようになります。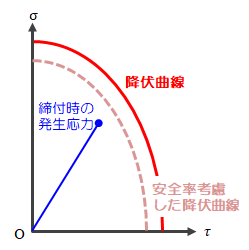
図2.7.1-1 ボルト軸部の降伏線図
軸部の断面径はねじ有効断面積径\(D_4\)と軸径\(D_{ax} \ \)の小さい方を用いて、引張り応力、せん断応力を求めます。\[
\sigma_{tf}
=
\frac{4F_ax}{\pi D_{min}^2 }
, \
\tau_{tf}
=
\frac{16T_{thf}}{\pi {D_{min}}^3 }
\\
(D_{min} = min(D_4, D_{ax} ))
\]
締付時の発生応力評価は、Webアプリページ
締付トルク(詳細版)
で公開していますので、ご活用ください。
2.7.2.ねじ山せん断応力
ボルトを締めすぎると、ねじ山がつぶれてしまうことがあります。 これはねじの軸方向に力が作用すると、ねじ部にはせん断応力が発生するためです。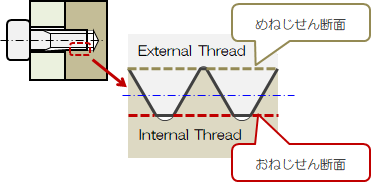
図2.7.2-1 ねじ山のせん断
おねじ、めねじのせん断に対する断面積は次のようにして求めます。\[
\large{\text{おねじ}} \normalsize{:} A_{in} = \pi D_1 \{ \frac{P}{2} + ( D_2 - D_1 ) \tan\alpha \} \frac{L_{eng}}{P} \\
\large{\text{めねじ}} \normalsize{:} A_{ex} = \pi D \{ \frac{P}{2} + ( D - D_2 ) \tan\alpha \} \frac{L_{eng}}{P}
\]
\[
\begin{eqnarray}
\left(
\begin{array}{lll}
D \large{\text{:呼び径、}} \hspace{20pt} &
D_1 \large{\text{:めねじ内径基準、}} \\
D_2 \large{\text{:有効径、}} \hspace{20pt} &
D_{fl2} \large{\text{:座面有効径}} \hspace{15pt} \\
P \large{\text{:ねじピッチ、}} &
\alpha \large{\text{:ねじ山半角}} \normalsize{(30°)、} \hspace{30pt} &
L_{eng} \large{\text{:かみ合い長さ}} \hspace{30pt}
\end{array}
\right)
\end{eqnarray}
\]
ねじ山に加わる荷重は軸力を\(F_{ax} \ \)、引張り荷重を\(F_t\)とするとき、\[
\begin{eqnarray}
F_{eng} =
\begin{cases}
F_{ax} + \phi F_t \quad \large{\text{(遊離していない場合)}}\\
F_t \large{\text{(遊離した場合)}}
\end{cases}
\end{eqnarray}
\]
となります。ねじ面は斜面であるからせん断面に作用する荷重は、次のようになります。\[
(1 + \mu_{th} \tan\alpha ) F_{eng}
\]
また、応力はかみ合い部に均等に発生するわけではなく、ねじ先端側ほど荷重分担が小さくなります
(サイト検索で「ねじ CAE」と打つと、いろいろな検証結果が表示されます)。
従って、かみ合い長さに対してかみ合い率\(\eta_{eng} \ \)を設定することで応力の分担を調整します。
例えば、かみ合い長さが1.3d以下と短い場合はかみ合い率を0.8程度、かみ合い長さが2d以上と長い場合は0.5程度をかみ合い長さに掛けるのが良いと考えられます。以上をもとに、せん断応力を算出します。
\[
\tau_i = \frac{(1 + \mu_{th} \tan\alpha ) F_{eng}}{\eta_{eng} \ A_i } \quad (i=ex,in)
\]
なお、ねじ山に発生する応力の算出は、Webアプリページ
ねじ山発生応力
ページで公開していますので、ご活用ください。
2.7.3.外力による発生応力
図2.7.3-1にねじに付加される荷重の種類を示します。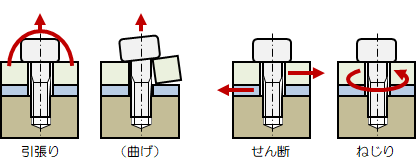
図2.7.3-1 ねじに働く外力
これらの外力が作用しても、ボルト、被締結体、ナットに塑性変形や破損などが生じないように設計する必要があります。(1)引張り荷重
締結時、締結体には軸力が作用しプリロードがかかっているため、 2.5節 でみたように引張り荷重\(F_t\)がすべて締結体に作用するわけではなく、内外力比\( \phi \)(<1)を掛けた分のみ軸力\(F_{ax} \ \)に上乗せされることになります。\[
\sigma_t = \frac{ 4 ( F_{ax} + \phi F_t )}{\pi D_{min}^2}
\]
引張り荷重については、破断よりもまずは降伏させないことを重視します。
ボルトが塑性変形すると永久ひずみが生じ、荷重を抜いても元の長さに戻らないことから軸力低下につながるためです。塑性域を積極的に用いた塑性域締付法(4章)もありますが、これは締付時のばらつきを抑えることが目的です。 変動荷重が大きい場合や衝撃荷重が作用するようなところでの使用は避けた方がよい、と考えています。
(2)曲げ荷重
圧力容器の締付などのように、ねじの軸線からずれたところに引張り荷重が生じるようなケースです。 このとき、ボルトには引張りと圧縮の両方が軸対象に作用します。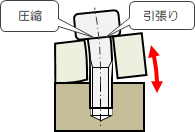
図2.7.3-2 曲げ荷重の例
この計算はモデル化が難しく、汎用的な計算ツールを作りづらく、用途に応じて都度計算ツールを作るのが一般的です。 また、CAEを活用するのも一つの手段です。(3)せん断荷重
せん断荷重はプリロードの影響を受けません。 被締結体がすべらない限り作用しません。 ただ、何等かの影響ですべりが発生したとしてもボルトが破損しないようにすることで、トラブルの発生を抑制することができます。また特殊事例として、座面の摩擦だけでは部品のすべりを抑えきれないような場合、キリ穴とボルト軸部がしまりばめになるリーマボルトを用いることがあります。
(4)ねじり荷重
これは主にシャフトに重いもの(慣性モーメントが大きいもの)を取り付けた際に生じる荷重です (例えば、クランクシャフトにフライホイールを取り付けるような場合)。 この場合、軸部にねじり荷重が発生します。ただし、せん断のときと同様、被締結体がすべらない限りねじり荷重は作用しません。 また、作用反作用の関係から、座面トルク以上のねじりトルクがボルトの軸部に作用することはありません。2.7.3.安全率
ねじに作用する荷重がどのような種類、性質なのかによって、安全率の設定は異なります。 表2.7.3-1に荷重の性質に対する安全率の例について示します。表2.7.3-1 ねじに働く荷重の性質(安全率の値は例とする)
| 負荷の種類 | 説明 | 例 | 安全率 |
|---|---|---|---|
| 静的荷重 | ねじ部に大荷重が静的に作用する。 | クレーン吊り下げ部(アイボルト)、圧力容器の締結部 | 1.5 |
| 繰返し荷重 | 振動環境等に曝され、ねじ部に繰返し荷重が作用する。 | 車等の各部締結部、ロケットや人工衛星の各締結部 | 2 |
| 衝撃荷重 | ねじ部に衝撃的な荷重が作用する。 | エンジンシリンダ締結部、火工品締結部、シートベルト固定部 | 10 |
2.7.4.温度負荷による影響
使用する温度条件によって、以下のような強度的懸念事項が考えられます。- 膨張差による応力の発生(熱応力)
- 材料特性の変化(弾性率や強度)
- 高温時のクリープ応力
- 低温時の脆性破壊等
(3)については部品に生じている応力が、使用時間と使用温度でのクリープ強度以下であることを確認します。
2.8.その他の観点
設計したねじがカタログ品で対応できればそれにこしたことはありません。 特に大量生産品であれば簡単に安く入手できます。 また大量生産≒使用実績となる場合が多いことから、品質保証の観点からも望ましいと考えられます。 まずはカタログ品などの大量流通品から選択可能かを検討します。流通品では対応できない場合、ねじを新作することを検討します。 その場合は2章で行った計算を元に、さらに生産性(製造の可否、値段の高低など)を考慮して設計していきます。 その場合はねじの材質、表面処理、熱処理、加工等製造に対する知識が必要となります。


