材料力学
1.材料力学の基本則
1.1.材料力学とは?
1.1.1.材料力学の目的
私たちの周囲にある機械や構造物は、その使用環境に応じた力の作用を受け変形します。 変形は自然の摂理として必ず生じるもので、有益な場合もあれば有害な場合もあります。 有益な変形には、ねじによる締結や、ばねによる蓄力といった例が挙げられます。 それに対し有害な変形には、機器の干渉や破壊といった重篤な問題を生じるものが挙げられます。 特に有害な変形に対しては、構造を頑丈にすることで問題を克服できますが、 材料を不必要に使用することになり、経済性を損なうことにつながります。 そこで、以下に示す観点を持って、機械や構造物を設計することになります。- 機械や構造物にどのような力が作用するか?
- その力によって機械や構造物にどのような変形が生じるか?
- この変形によって、機械や構造物は壊れないか?
- この変形によって、機械や構造物の機能に支障は出ないか?
1.1.2.材料力学の前提
材料力学では、次の仮定に基づき話が進められます。- 材料の均質性:材料内の性質はどこも均一で等しい
- 材料の等方性:材料内の性質は方向によって変化しない
- 材料の連続性:材料内に空洞や異物は存在しない
1.2.荷重・応力・ひずみ
1.2.1.荷重
荷重とは、物体に働く外力のことです。 一般的な荷重の分類は、(1)作用形態によるもの、(2)時間変化によるもので行われます。(1)作用形態によるもの
| 荷重 | 特徴 | 図 |
|---|---|---|
| 引張荷重 | 引っ張る方向に作用する力 |  |
| 圧縮荷重 | 圧縮する方向に作用する力 |  |
| せん断荷重 | 切断する方向に作用する力 | 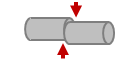 |
| 曲げ荷重 | 曲げる方向に作用する力 |  |
| ねじり荷重 | ねじる方向に作用する力 |  |
※引張荷重と圧縮荷重をまとめて垂直荷重といいます。
(2)時間変化によるもの
| 荷重 | 特徴 |
|---|---|
| 静荷重 | 力の大きさや方向が時間的に変化しない(と見れる)荷重 |
| 動荷重 | 力の大きさや方向が時間的に変動する荷重 |
| i)繰り返し荷重 | 荷重方向は変わらず、大きさのみ周期的に変化する荷重 (引張だけ、圧縮だけ...など) |
| ii)交番荷重 | 荷重の方向、大きさともに周期的に変化する荷重 (引張/圧縮の繰り返し) |
| iii)衝撃荷重 | 極めて短時間に、半正弦波的に作用する荷重 |
1.2.2.応力
物体に荷重(外力)が作用すると、作用反作用の法則に従い物体内部にも力が生じます。 これを内力と呼び、単位断面積あたりの内力を応力と呼びます。\[
応力
=
\frac{ 内力 }{ 断面積 }
\tag{1.2.2-1}
\]
応力は、断面に作用する向きによって、“垂直応力”と“せん断応力”の2つに分類されます。| 垂直応力 | せん断応力 | |
|---|---|---|
| 図 | 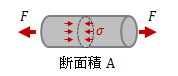 |
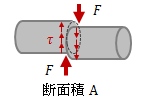 |
| 荷重方向 | 断面に対して垂直に作用(面外方向) | 断面に対して平行に作用(面内方向) |
| 式 | \( \sigma = \frac{ F }{ A } \) | \( \tau = \frac{ F }{ A } \) |
| その他 | 力Fが引張→σは引張応力 力Fが圧縮→σは圧縮応力 |
1.2.3.変位とひずみ
変位とは、空間上のある着目点が別の場所へ移動する際に生じるずれのことです。 物体に荷重を加えると、多かれ少なかれ必ず変形します。 この変形とは、物体内部のある点に変位が生じることです。 ただし、物体内部のすべての点が同じ変位を持つ場合は変形とはなりません。 この場合、物体全体が運動していることに他なりません。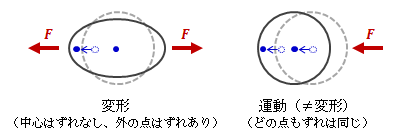
図1.2.3-1 物体の変形
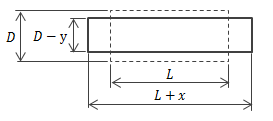
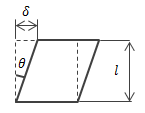
そのため、物体の変形を評価するには変位ではなく別のパラメータで評価する必要があります。 これがひずみになります。 ひずみとは、物体の変形枚の寸法に対する変形量の割合を表すもので、 その定義から無次元であることがわかります。 また、ひずみの大小によって、物体内の任意の位置における変位の度合いを知ることができます。 さて、物体に垂直荷重を与えるとき、荷重方向に対して伸び縮みするだけでなく、 荷重と直交する方向にも伸び縮みが発生します。 例えば、一様な丸棒に引張荷重を付加すると、荷重方向に棒は伸びるとともに、 直交方向は棒が細くなり、縮みます。 また、せん断ひずみについては、形状のゆがみを表しています。 このようにひずみには方向性があり、その方向によって“縦ひずみ”、 “横ひずみ”、“せん断ひすみ”の3種類に分類されます。| 縦ひずみ | 横ひずみ | せん断んひずみ |
|---|---|---|
 |
 |
|
| \( \epsilon = \frac{ x }{ L } \) | \( \epsilon ' = \frac{ t }{ d } \) | \( \gamma = \displaystyle \frac{ \delta }{ l } = tan \theta \simeq \theta \) |
\[
\nu
=
\frac{ \epsilon ' }{ \epsilon }
\tag{1.2.3-1}
\]
また、ポアソン比の逆数をポアソン数と呼びます。
ポアソン比は材料固有の物性値であり、次節で出てくる縦弾性係数と横弾性係数に密接に関連します。
1.3.荷重と変形の関係
1.3.1.弾性と塑性
変形している物体ら荷重を除いたとき(除荷)、完全に元の状態に戻る、 つまり変形のない状態に戻る性質を弾性といいます。 それに対し、除荷しても変形が残留する性質を塑性といいます。 一般に材料は、応力がある値を超えるまでは弾性を示し、それを超えると塑性を示すようになります。 この分岐となる応力を弾性限度と呼びます。 実際は弾性限度を明確に知ることはできないため、それに準ずる応力によって弾性域かどうかを判定します (詳細は1.4章)。1.3.2.フックの法則
力学でもよく知られているフックの法則とは、 物体に加えた力とそれにより生じる変位が比例関係にあることを言います。 この比例関係は付加/除荷のどちらでも成り立たなければなりませんので、 弾性範囲内でのみ成立する法則になります。 力学におけるフックの法則の公式は、力F、変位量x、ばね定数kとおいて\[
F = - k x
\tag{1.3.2-1}
\]
で表します。それに対し材料力学では、垂直応力σ、垂直ひずみεを用いて
\[
\sigma = E \epsilon
\tag{1.3.2-2}
\]
で表します。このときEは比例定数で、材料固有の値を表します。
このEを縦弾性係数あるいはヤング率と呼びます。
ひずみは無次元であることから、縦弾性係数は応力と同じ単位を持ちます。
今、長さLの一様断面積Aを有する棒に、引張荷重Fを作用させたときの伸びをxで表す時、(1.3.2-2)式は次のように書き換えられます。
\[
\frac{ F }{ A }
=
E \frac{ x }{ L }
\
\rightarrow
\
F
=
\frac{ EA }{ L } x
\tag{1.3.2-3}
\]
(1.3.2-1)式と比較するとわかるように、xの係数がばね定数に相当することがわかります。
また、フックの法則はせん断方向に対しても成り立ちます。せん断応力τ、せん断ひずみγとおいて、
\[
\tau
=
G \gamma
\tag{1.3.2-4}
\]
の関係が得られ、比例定数Gを横弾性係数あるいはせん断弾性係数と呼びます。
Gもまた材料固有の値になり、応力と同じ単位を持ちます。
材料固有の値である縦弾性係数Eと横弾性係数Gの間には、ポアソン比νと呼ばれる次式の関係があります。
\[
G
=
\frac{ E }{ 2 ( 1 + \nu ) }
\tag{1.3.2-5}
\]
この関係式によって、3つの値のうち2つが決まれば、残りの1つは算出できることになります。ここで、フックの法則に関する物理的解釈を付け加えておきます。 フックの法則は位置に関する一価関数であることから、保存力⊂ポテンシャルになります。 これは力学的エネルギー保存則が成り立つことを意味し、熱力学的観点から見れば可逆性が成り立つ系となります。 逆に言えば、変形が塑性域に入ると不可逆性が顕著に表れることを意味しています。
1.3.3.ひずみエネルギー
物体に荷重が作用し変形する過程をエネルギーの観点から捉えてみます。 このとき、荷重は物体を変形させるだけの仕事を行い、 それに対応して物体内部に発生したひずみによってエネルギーが蓄積された、と考えることができます。 このエネルギーをひずみエネルギーと呼びます。 ひずみエネルギーは、(1.3.2-3)式を変位で積分することで求められます。\[
U
=
\int_0^x F ( x ) dx
=
\int_0^x \frac{ EA }{ L } x dx
\tag{1.3.3-1}
\]
特に弾性変形においては、xの係数は定数と見ることができるので、
\[
U
=
\frac{ E A }{ 2 L } x^2
\tag{1.3.3-2}
\]
で表すことができます。
このとき荷重と変位は線形関係にあるため、下図の赤斜線部の面積がひずみエネルギーに該当します。
それに対し弾性変形でない場合は、一般に荷重と変位が非線形となり、例えば(赤+青斜線部)
の面積がひずみエネルギーとなります。
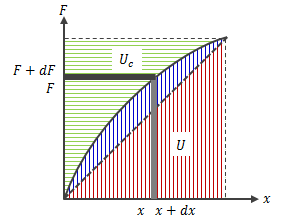
図1.3.3-1 ひずみエネルギー
ひずみエネルギーは変位xを変数として積分したエネルギーUに該当するのに対し、 力Fを変数とした積分エネルギーUc(上図緑斜線部)を コンプリメンタリエネルギーと呼び、次式で表します。\[
U_c
=
\int_0^F x ( F ) dF
=
\int_0^F \frac{ L }{ EA } F dF
\tag{1.3.3-3}
\]
ひずみエネルギーUとコンプリメンタリエネルギーUcの和は、常に上図四角形(全斜線部)の面積に該当します。
UcはUに対し相補的(Complementary)であることが、その名前の由来になります。
さらに、U、Ucの定義から、次式に基づき荷重Fと変位xを求めることができます。
\[
\frac{ \partial U }{ \partial x } = F
,
\frac{ \partial U_c }{ \partial F } = x
\tag{1.3.3-4}
\]
また、変形がフックの法則に従うとき、(1.3.3-3)式に(1.3.2-3)式を代入することで、
\[
U_c
=
\frac{ L }{ 2 E A } F^2
=
\frac{ L }{ 2 E A } \biggl( \frac{ E A }{ L } x \biggr)^2
=
U
\tag{1.3.3-5}
\]
ひずみエネルギーUとコンプリメンタリエネルギーUcは一致します。
以上のエネルギーの考え方は、後述する(予定の)カスティリアノの定理を用いた不静定問題で用いられます。


