1.塑性変形
1.1.塑性変形概要
一般に固体材料は、ある荷重の範囲内で弾性変形します。 しかしその荷重を超えると、荷重を取り除いても変形が残るようになります。 このような変形を塑性変形といいます。 下図に、ある金属材料の応力-ひずみ線図を示します。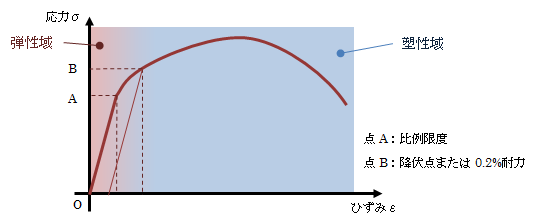
図1.1-1 応力-ひずみ線図
上図のように、点Bの降伏点通過後引き続き変形を増大させるには、 一般に荷重を増加させる必要があります。 このような特性をひずみ硬化または加工硬化と呼びます。次に材料を塑性変形させた後荷重を0にし、また荷重を掛けた場合について見ていきます。
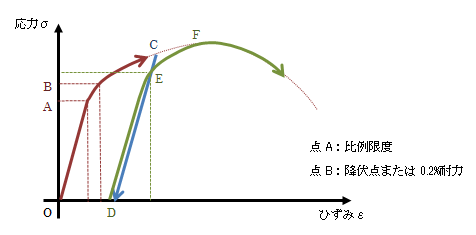
図1.1-2 塑性変形における応力-ひずみ線図
点Cまで塑性変形させた後荷重を0にすると、上図のように弾性応答とほぼ平行にひずみが減少します。 これは次のような理由によるものです。- 点O→Aの変形は、材料内部で均質に結晶粒の弾性変形が生じます。
- 点A→B→Cでは、材料内部で結晶粒の降伏が非均質的に生じます。
- 点C→Dへ移行するとき、材料内部には弾性変形と塑性変形の両方が存在し、 特に塑性変形部は材料内に不均一に存在します。
- 点D→E→Fへ移行すると、D→Eの変形は新しい比例限度E を伴ってその範囲でO→Aに平行な弾性変形を起こします。 点Eから先は新たな降伏が発生し、最終的に点Fで曲線BCの特性に従い変形が進展します。
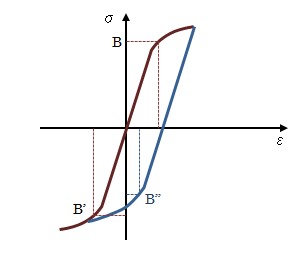
図1.1-3 バウシンガー効果
上図のように、塑性変形後もとの荷重と逆向きの荷重を掛けると降伏点B’’が現れますが、その応力は降伏前の材料の降伏点B’よりも絶対値として小さくなるのが一般的です。 このように、荷重の方向性によって塑性特性が決まる現象をバウシンガー効果と呼びます。1.2.真応力と対数ひずみ
単純引張り試験における応力-ひずみ線図を考えます。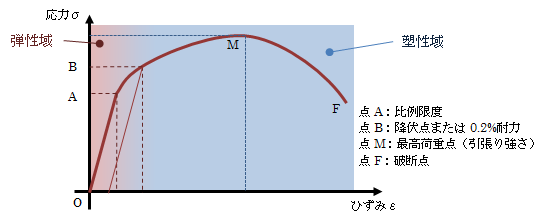
図1.2-1 公称応力-ひずみ線図
これまでの応力-ひずみ線図は“公称応力-ひずみ線図”を暗黙知としていました。 この公称応力-ひずみ線図に対する降伏応力、引張り強さ、伸び率、断面縮小率は次のように求められます。| 降伏応力 | \[ \sigma_y = \frac{P_y}{A_o} \] |
| 引張り強さ | \[ \sigma_{\mu} = \frac{P_{\mu}}{A_o} \] |
| 伸び率 | \[ \phi_F = \frac{l_F-k_o}{l_o} \] |
| 断面縮小率 | \[ g_F = \frac{A_F-A_o}{A_o} \] |
(\( A_o, l_o \):変形前の断面積、長さ)
材料の変形があまり大きくない場合は、A0、l0を基準に上記パラメータを算出しても特に問題はありませんが、変形が大きくなると公称値が材料固有の特性を示すとは言い難くなります。 実際に材料に発生する応力は、ある時点での断面積をAとして
\[
\sigma
=
\frac{P}{A}
\]
で表され、この応力を公称応力に対して真応力と呼びます。
また各瞬間での材料の長さをlとし長さの変化量をdlとすれば、その時点でのひずみはdl/lで表せます。
これをl0からlの範囲で足し合わせると、\[
\epsilon
=
\int_{l_o}^l \frac{dl}{l}
=
\ln \frac{l}{l_o}
\]
となります。このひずみを公称ひずみに対し対数ひずみまたは自然ひずみと呼びます。
真応力、対数ひずみは大きな変形扱う際必要な考え方になります。
1.3.弾塑性挙動の基礎モデル
1.3.1.塑性挙動の理想化
金属材料の塑性挙動は複雑なため、必要な特性を保持した状態で理想化・単純化します。 ここでは応力-ひずみ特性について、次の4通りの理想化モデルを示します。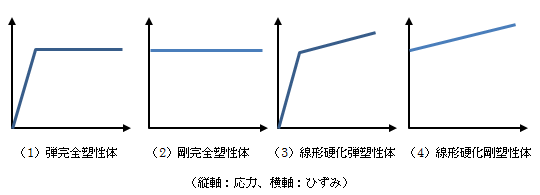
図1.3.1-1 塑性挙動の理想化モデル
これらの理想化にはT.P.O.があります。やみくもに適用するのではなく、直面する課題や解析手法に合わせて選択する必要があります。1.3.2.降伏の条件
金属は単結晶の集合体であり、これをいくつかの部材(トラス)によって構成された構造体として簡略モデル化することで、数学的に塑性挙動を考察することが可能になります。そこで、下図のような3部材のトラス構造を考えます。トラスはすべて同一材、同一断面積とします。 これは不静定構造ゆえ、それぞれの部材の変形を考慮する必要があります。
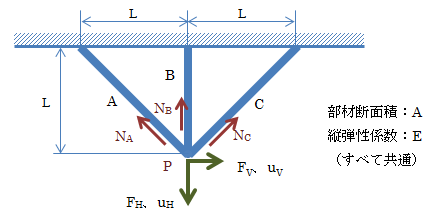
図1.3.2-1 金属の簡易モデル化
上図のように、点Pに荷重Fが作用したとき、その変位をuとします。 このとき、各部材に働く内力をNA、NB、NC(スカラー)、ひずみをεA、εB、εCとすると、点Pでの力のつり合いは次のようになります。\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{\sqrt{2}}{2} N_A + N_B + \frac{\sqrt{2}}{2}N_c
=
F_V
\\
\displaystyle \frac{\sqrt{2}}{2} \left( N_A - N_C \right )
=
F_H
\end{array}
\right.
\end{eqnarray}
\]
また、変位とひずみの関係は次のとおりです。\[
\begin{eqnarray}
\left.
\begin{array}{l}
\epsilon_A
=
\displaystyle \frac{1}{2L} (u_v + u_H) \
\\
\\
\epsilon_B
=
\displaystyle \frac{u_v}{L}
\\
\\
\epsilon_C
=
\displaystyle \frac{1}{2L} (u_v - u_H) \
\end{array}
\right\}
\rightarrow
\epsilon_A + \epsilon_C
=
\epsilon_B
\end{eqnarray}
\]
さらに、応力とひずみの関係式(σ=Eε)からNA、NB、NCが決まります。\[
\begin{eqnarray}
\left.
\begin{array}{l}
N_A
=
\displaystyle \frac{\sqrt{2}F_V}{2(1+\sqrt{2})} + \frac{F_H}{\sqrt{2}}
\\
\\
N_B
=
\displaystyle \frac{\sqrt{2}F_V}{2(1+\sqrt{2})}
\\
\\
N_C
=
\displaystyle \frac{\sqrt{2}F_V}{2(1+\sqrt{2})} - \frac{F_H}{\sqrt{2}}
\end{array}
\right.
\end{eqnarray}
\tag{1.3.2-1}
\]
上式は弾性変形内において成立するものです。さて、ここでトラスの降伏条件を考えます。 このときの塑性挙動モデルは1.3.1項で述べた“弾完全塑性体”であると仮定します。
トラスの降伏応力をσy、それに相当するトラスの内力をNy=Aσyとします。 すると、次の3式のうちどれか一つが成り立つと、部材は降伏を始めます。
NA=±Ny、NB=±Ny、NC=±Ny
今、F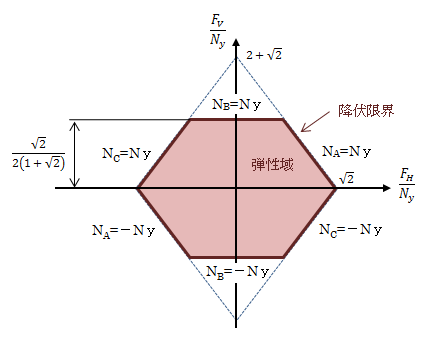
図1.3.2-2 トラスの弾性変形範囲
点Pに負荷される荷重Fがこの六角形の領域より外に出ようとした瞬間、 トラスに降伏が発生します。ここで1つの例として、FH=0のままFVを増加させる場合を考えます。 すると、六角形領域の外枠に最初に到達するのはFV=Nyのときで、このときNB=Nyになります。このときの外力と変位は次のようになります。
\[
\begin{eqnarray}
\left.
\begin{array}{l}
F_{V1}
=
\displaystyle \frac{(1+\sqrt{2})}{\sqrt{2}} \ N_y
\\
\\
u_{V1}
=
\displaystyle \frac{\sqrt{2}}{1+\sqrt{2}} \ \frac{L F_{V1}}{AE}
\end{array}
\right.
\end{eqnarray}
\tag{1.3.2-1}
\]
FVがFV1を超えるとき部材Bは降伏し、塑性挙動の前提として弾完全塑性体としていることから、それ以降部材Bに発生する内力はNy一定となります。
そのため、FV1<FVで部材A、Cに働く内力と点Pの垂直方向変位は次のようになります。\[
\begin{eqnarray}
\left.
\begin{array}{l}
N_A
=
N_C
=
\displaystyle \frac{\sqrt{2}}{2} (F_V - N_y)
\\
\\
u_V
=
\displaystyle \frac{\sqrt{2} \ L}{2AE} (F_V - N_y)
\end{array}
\right.
\end{eqnarray}
\]
水平方向に外力は働かないので部材A、Cは対称性を持ちます。
よって、NA=NCが成り立ちます。
つまり、部材AとCは同時に降伏を起こすことになります。
このAとCが同時に降伏を起こす時の外力は次のようになります。\[
F_{V2}
=
\frac{(2+\sqrt{2})}{\sqrt{2}} \ N_y
\]
以上をまとめると次のようになります。
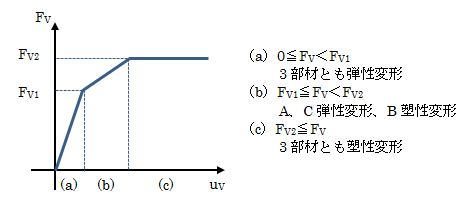 上記(c)になるとすべての部材が降伏しているため、無制限に変形を進めてしまう危険性があります。
このような状態を塑性崩壊といいます。
上記(c)になるとすべての部材が降伏しているため、無制限に変形を進めてしまう危険性があります。
このような状態を塑性崩壊といいます。これまでは3部材で検討しましたが、 部材数を増やせば(b)領域の直線が多角化→曲線化され、弾性→塑性域移行時の応力-ひずみ線図に似通ってきます。 以上が簡易数学モデルによる降伏条件の考え方になります。


