材料力学
2．厚肉円筒
下図の厚肉円筒に、内圧と外圧が作用することで生じる応力と変形量を求めてみます。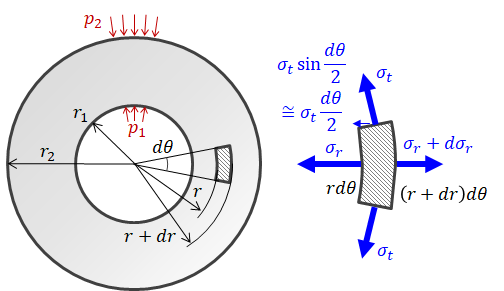
厚肉円筒内の微小要素に作用する応力は、径方向応力\( \sigma_r \)、周方向応力\( \sigma_t \)の2成分で表現できます。
このとき、微小要素に対する径方向の力のつりあい式は次のようになります。
\[
( \sigma_r + d \sigma_r ) ( r + dr ) d \theta
- \sigma_r r d \theta - 2 \sigma_t \frac { d \theta }{ 2 } dr = 0
\tag{2-1}
\]
特に\( \sigma_t \)の項は、微小要素が曲がっていることによって生じるもので、忘れないように注意する必要があります。
この式を地道に展開計算し
\[
\begin{align}
(1)式
& =
( \sigma_r r + \sigma_r dr + r d \sigma_r + dr d \sigma_r ) d \theta
- \sigma_r r d \theta - \sigma_t d \theta dr
\\
& =
\sigma_r dr d \theta + r d \sigma_r d \theta + dr d \sigma_r d \theta - \sigma_t d \theta dr
\\
& \simeq
( \sigma_r dr - \sigma_t dr + r d \sigma_r ) d \theta
\\
& = 0
\end{align}
\]
以上の計算から、次の微分方程式が得られます。
\[
r \frac{ d \sigma_r }{ dr }
=
\sigma_t - \sigma_r
\tag{2}
\]
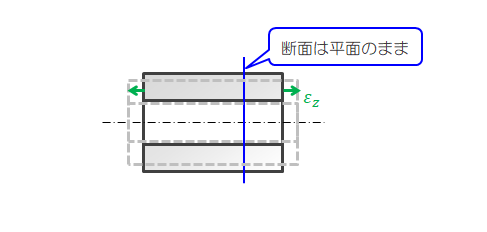
ところで、断面は円筒が変形しても平面を保つものと仮定すると、軸方向のひずみ\( \epsilon_z \)は一定になります。
軸方向応力を\( \sigma_z \)とおいて、\( \epsilon_z \)は次のように表せます。
\[
\frac{ 1 }{ E } \{ \sigma_z - \nu ( \sigma_t + \sigma_r ) \}
=
\epsilon_z
=
const
\tag{3}
\]
さて、円筒の両端が開放されていれば\( \sigma_z = 0 \)であるし、固定されていれば\( \sigma_z \)は
\[
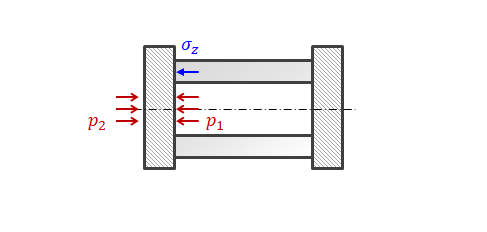
\pi ( r_2^2 - r_1^2 ) \sigma_z
=
\pi r_2^2 p_2 - \pi r_1^2 p_1
\
\rightarrow
\
\sigma_z
=
\frac{ r_2^2 p_2 - r_1^2 p_1 }{ r_2^2 - r_1^2 }
\tag{4}
\]
で定まり、一定になります。
この結果を考慮して（3）式を変形することで、\( \sigma_t, \sigma_r \)の次の関係式が得られます。
\[
\sigma_t + \sigma_r
=
2 \lambda
=
const
\tag{5}
\]
（2）、（5）式から\( \sigma_t \)を消去すると
\[
r \frac{ d \sigma_r }{ dr }
=
2 \lambda - 2 \sigma_r
\]
この両辺に\( r \)を掛ければ
\[
r^2 \frac{ d \sigma_r }{ dr } + 2 r \sigma_r
=
2 \lambda r
\
\rightarrow
\
\frac{ d }{ dr } ( r^2 \sigma_r )
=
2 \lambda r
\tag{6}
\]
が得られます。（6）式を積分定数\( C \)を用いて積分することで
\[
r^2 \sigma_r
=
\lambda r^2 + C
\tag{7}
\]
が得られます。
ここで\( \lambda , C \)を求めるために内圧と外圧の境界条件を用います。
\( r = r_1 \)のとき、\( \sigma_r = -p_1, r = r_2 \)のとき\( \sigma_r = - p_2 \)であるから
\[
\begin{cases}
r_1^2 p_1
=
\lambda r_1^2 + C
\\
\\
r_2^2 p_2
=
\lambda r_2^2 + C
\end{cases}
\qquad
\rightarrow
\qquad
\begin{cases}
\lambda
=
\displaystyle
\frac{ p_1 r_1^2 - p_2 r_2^2 }{ r_2^2 - r_1^2 }
\\
C
=
\displaystyle
\frac{ ( p_1 - p_2 ) r_1^2 r_2^2 }{ r_2^2 - r_1^2 }
\end{cases}
\]
が得られます。
この\( \lambda, C \)を（7）式に代入することで\( \sigma_r \)が、さらにこの\( \sigma_r \)を（5）に代入すれば\( \sigma_t \)が求まります。
\[
\begin{align}
& \sigma_r
=
- \frac{ p_1 r_1^2 ( r_2^2 - r^2 ) + p_2 r_2^2 ( r^2 - r_1^2 ) }
{ r^2 ( r_2^2 - r_1^2 ) }
\\
& \sigma_t
=
\frac{ p_1 r_1^2 ( r_2^2 + r^2 ) - p_2 r_2^2 ( r^2 + r_1^2 ) }
{ r^2 ( r_2^2 - r_1^2 ) }
\end{align}
\tag{8}
\]
最後に変形量\( u \)を求めます。
周方向ひずみ\( \epsilon_t \)は周長が\( 2 \pi r \)から\( 2 \pi ( r + u ) \)に変化することから、径方向歪み\( \epsilon_r \)は
\[
\epsilon_t
=
\frac{ 2 \pi ( r + u ) - 2 \pi r }{ 2 \pi r }
\
=
\frac{ u }{ r }
\tag{9}
\]
径方向歪み\( \epsilon_r \)について、\( r \)での変位\( u ( r ) \)に対して\( r + dr \)での変位\( u ( r + dr ) \)は
\[
u ( r + dr ) - u( r )
\simeq
\frac{ du }{ dr } dr
\tag{9}
\]
で表せるので
\[
\epsilon_r
=
\frac{ ( u + \displaystyle \frac{ du }{ dr } dr ) - u }{ dr }
=
\frac{ du }{ dr }
\tag{10}
\]
ひずみと応力の関係式は
\[
\epsilon_r
=
\frac { 1 }{ E }
\{ \sigma_t - \nu ( \sigma_r + \sigma_z ) \}
\tag{11}
\]
であるから、応力の式（4）式と（9）式を上式に代入して頑張って計算すると、
\[
u
=
\frac{ ( 1 + \nu )( p_1 - p_2 ) }{ E }
\frac{ r_1^2 r_2^2 }{ ( r_2^2 - r_1^2 ) r }
+
\frac{ ( 1 - \nu ) }{ E }
\frac{ ( p_1 r_1^2 - p_2 r_2^2 ) }{ ( r_2^2 - r_1^2 ) } r
- \frac{ \nu \sigma_z }{ E } r
\tag{12}
\]
が得られます。
なお、軸方向応力\( \sigma_z \)は境界条件に応じて0または（8）式で定まります。
