材料力学
1.材料力学の基本則
1.4.材料の機械的性質
1.4.1.強度と剛性
機械や構造物を設計する際、必ず出てくる言葉が“強度”と“剛性”です。 これらは別の意味を表しているのですが、よく混同して用いられているので、ここではその違いを明確に示します。 “強度”とは材料の強さであり、応力によって表します。 例えば、物体に引張荷重が作用したときの引張強さとは、物体が壊れるまでの間に発生する最大応力のことです。 それに対し“剛性”とは物体の変形し難さであり、その表し方は弾性係数を用いたり、 固有振動数を用いたり、ひずみを用いたりと様々ですが、応力で表すことはありません。例えば同じ強度のものでも剛性が違うものはいくらでもあります。 例えば、鋼(S45C)と超々ジュラルミン(A7075-T6)を比較してみます。
| 材質 | 引張強さ (MPa) |
縦弾性係数 (GPa) |
処理 |
|---|---|---|---|
| S35C | 570 | 206 | 焼き入れ焼き戻し処理 |
| A7075 | 570 | 71 | T6処理 |
1.4.2.応力-ひずみ曲線
材料は、それぞれに固有の応力-ひずみ特性を持っています。 この特性を表す応力-ひずみ曲線は、JIS Z 2241「金属材料引張試験」で規定された引張試験方法によってプロットされるものです。 この曲線は、金属材料だけでなく、セラミックスやゴム、プラスチック等でも用いられます。 材料は、その変形度合によってさまざまな性質を示します。 そこで、下図に示す軟鋼とアルミの応力-ひずみ曲線上に示される点に従って、その特徴を見ていくことにします。
図1.4.2-1 応力-ひずみ曲線
まず、鋼の応力-ひずみ曲線について見ていきます。 OP間は応力とひずみが線形(比例)関係にあり、フックの法則が成立する範囲になります。 そのため点Pの応力を比例限度と呼びます。 点Eは、線形関係は崩れるものの応力を除荷すれば元の状態に戻る限界で、弾性限度と呼びます。 さらに荷重を上げると、ひずみが増えるにもかかわらず応力は増加しない領域YU~YLが現れます。 この点を降伏点とよび、特に軟鋼等に現れるYUを上降伏点、YLを下降伏点と呼び、一般に降伏点は上降伏点のことを指します。 この降伏点を超え、さらに荷重を上げたところでは、図の上で2本の線が現れます。 実線は、荷重を与える前の断面積で応力を算出したもので公称応力と呼び、 破線は変形に伴い減少する断面積で応力を算出したもので真応力と呼びます。 一般に材料特性としては公称応力を用いた応力-ひずみ曲線が用いられます。 YLからMの範囲では、加工硬化(ひずみ硬化)を生じながら、応力-ひずみの関係を非線形化し極大点Mに到達します。 このMは引張試験における最大応力を示すことから、引張強さまたは極限強さと呼びます。 最後に、M点を超え試験片を引っ張ると、巨視的に見ても明らかに試験片の一部が細くくびれはじめ、急速に断面積が減少し、試験片は破断します。 また、アルミでは降伏点は顕在化しないため、一定の永久ひずみ(一般に0.2%)が生ずる応力を降伏点として代用します。 このような点Y0.2を耐力と呼びます。1.4.3.その他の材料の性質
材料には次のような性質があります。| 種類 | 性質 | 特徴 | 例 |
|---|---|---|---|
| 延性 | 弾性限度を超えて破壊に至るまでの変形が大きい | 引張と圧縮の弾性的性質にあまり差はない | アルミ、銅、金など |
| 脆性 (ぜい性) |
脆く、破壊にいたるまでの変形が少ない | 圧縮強さは引張強さの数倍に達する | コンクリート、セラミックスなど |
| 靱性 (じん性) |
粘り強く、破壊しにくい耐衝撃性に優れる | 亀裂の進展が遅く、高強度かつ延性が高い |
1.4.4.疲労破壊
どのような材料も繰り返し荷重を受けると、降伏応力以下でも破壊に至ります。 このような破壊を疲労破壊と呼びます。 疲労破壊は、繰り返し応力の大きさと繰り返し数によって決まり、応力が大きければ少ない繰り返し数で破壊に至ります。 それに対し、ある応力まで低減できれば、繰り返し数をいくら増やしても破壊に至りません。 この破壊に至らない最大応力を疲労限度と呼びます。 疲労破壊の挙動を調べるものとしてJIS Z 2273で規定される疲れ試験があります。 疲労破壊に対する評価は、繰り返し応力から平均応力と応力振幅を求めることから始まります。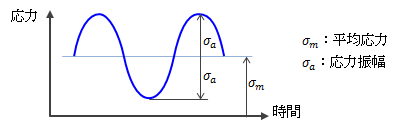
図1.4.4-1 繰り返し応力
平均応力を一定とし、応力振幅と繰り返し数によってプロットされたデータから、疲労破壊を生じない限界曲線が得られます。 この曲線をS-N曲線と呼びます。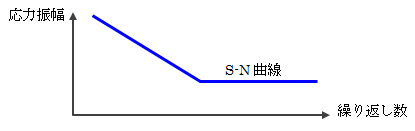
図1.4.4-2 S-N曲線
また、横軸に平均応力、縦軸に応力振幅をとり、繰り返し数ごとにデータをプロットすることで破壊を生じない限界曲線が得られます。 この曲線を耐久限度線(グッドマン線)と呼びます。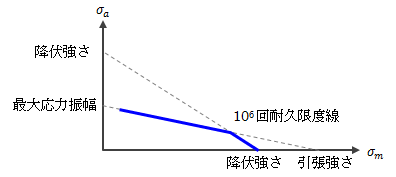
図1.4.4-3 耐久限度線
疲労破壊は、仮に弾性変形内の応力であったとしても、繰り返し作用することによって材料の一部に亀裂が生じ、 その亀裂の拡大とその部分に生じる応力集中により破壊に至る現象です。機械や構造物の破壊において、 疲労破壊が非常に多くの割合を占めていると言われており、設計において必ず注意を払わなければならない検討項目になります。1.4.5.応力集中と切欠き係数
断面が一様な材料に荷重を作用させた場合、すべての断面で応力は一様に作用します。 それに対し、急激な断面積変化が生じるようなところ、例えば、棒に溝や切欠き、穴等が開いている場合、 応力はこの周囲で局所的に増大します。このような状態を応力集中と呼びます。 応力集中によって亀裂が生じ破壊を起こしやすくすることから、曲率が小さいほど、また鋭角度合いが強いほど、 応力集中は大きくなります。 応力集中の度合いを評価するものとして、局所的に発生した最大応力σMAXを、 その応力発生個所を含む最小断面積の平均応力σmで割ったものとして応力集中係数(形状係数)αkを定義します\[
\sigma_k
=
\frac{ \sigma_{MAX} }{ \sigma_m }
\tag{1.4.5-1}
\]
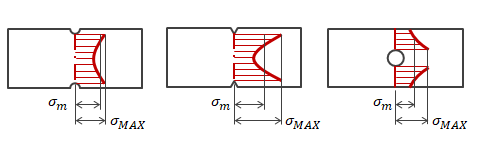
図1.4.5-1 応力集中の状態
応力集中係数と似たようなものに切欠き係数があります。 切欠き係数βは疲労強度の低下を表すものとして用いられ、切欠きがない場合とある場合の疲労強度の比で定義されます。\[
\beta
=
\frac{ 切り欠きがない場合の疲労強度 }{ 切り欠きがある場合の疲労強度 }
\tag{1.4.5-2}
\]
このように、応力集中係数と切欠き係数はその定義が異なります。
しかしながら、応力集中は切欠き等の断面積変化がある場所で生じ破壊の起点になりやすく、また、疲労破壊は切欠きから発生した亀裂が進展して破壊に至ることから、切欠き係数と応力集中係数に何らかの関係性を持つ、と考えるのはごく自然流れです。
実際に、引張強さごとに応力集中係数と切欠き係数の間には下図のような概念図に基づく関係があり*、
応力集中係数を求めることで、疲労強度の低下が求められることになります。
*:参考文献リンク
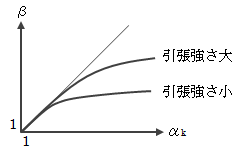
図1.4.5-2 切欠き係数と応力集中係数の関係
1.4.6.クリープ破壊
一定の応力で金属を引っ張ると、時間とともに塑性変形が進行する現象をクリープと呼びます。 クリープは高温になるにつれ生じやすくなり、降伏応力以下でも起きる現象です。 クリープは3つの過程に分けられます。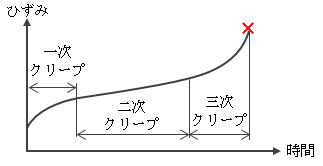
図1.4.6-1 クリープ特性
| 一次クリープ (遷移クリープ) |
負荷直後に発生する弾性伸び後、塑性変形が急速に発展し、その後変形速度が徐々に遅くなる範囲 |
| 二次クリープ (定常クリープ) |
変形速度が一定 |
| 三次クリープ (加速クリープ) |
変形速度が急速化するところからクリープ破断を起こすまで |
1.5.許容応力と安全率
機械や構造物の強度評価について、単純に材料強度以下の応力に収まっていればよい、というわけにはいきません。 JISの規定に従って得られた材料強度は、試験片に対して得られたものであって、実使用環境におけるものではありません。 つまり、あらゆる使用環境に対する保証強度ではない、ということです。 実際、材料のばらつきや寸法ばらつき、使用環境のばらつきなど、様々な不確定要素を考慮すれば、 実使用に耐えうる最大応力=許容応力σaは材料の基準強さσfに対してある比率Sを持って、 その安全性を確保しなければなりません。 この比率Sを安全率と呼び、通常1より大きい値を選びます。\[
S
=
\frac{ \sigma_a }{ \sigma_f }
( > 1 )
\tag{1.5-1}
\]
また、材料の基準強さについては、その使用条件から選び方が決まります。
ただし、これは製品の信頼性に直結するものであり、業界や会社の基準によって左右されることから、
設計者が置かれているルールに従って、材料の基準強さを選択する必要があります。


