ニューラルネットワーク
4．4．3．隠れ層を追加する
出力を1つに戻して、順を追って隠れ層を追加していきます。a）隠れ層を1層追加します。
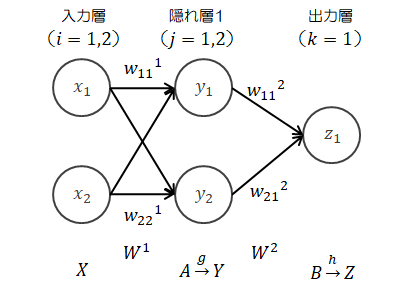
| 入力 | ： | \( X = (x_1, x_2) \in R^{1 \times 2} \) |
| 重み | ： | \( W^1 = \begin{pmatrix} w_{11}^1 & w_{12}^1 \\ w_{21}^1 & w_{22}^1 \end{pmatrix} \in R^{p \times q} \)、\( W^2 = \begin{pmatrix} w_{11}^2 \\ w_{21}^2 \end{pmatrix} \in R^{p \times q} \) |
| 重み付き総和 | ： | \( A=(a_1, a_2) \in R^{1 \times 2} \)、\( B=(b) \in R \) |
| 出力 | ： | \( Y=(y_1, y_2) \in R^{1 \times 2} \)、\( Z=h(b) \in R \) |
| 入力層→隠れ層1 | ： | \( A = XW^1 \) |
| 隠れ層1の処理 | ： | \( Y = g(A) \) |
| 隠れ層1→出力層 | ： | \( B = YW^2 \) |
| 出力層の処理 | ： | \( Z = h(B) \)または\( z = h(b) \) |
\( \displaystyle \frac{\partial L}{\partial W^2} \)は（4.4-1）式の\( X \)を\( Y \)に置き換えるだけです。
\[
\frac{\partial L}{\partial W^2}
=
Y^t \frac{\partial L}{\partial z} \{ h(b) \}'
\]
\( \displaystyle \frac{\partial L}{\partial W^1} \)は成分計算した方がわかりやすいので、まずは\( w_{11} \)に着目して計算してみます。\[
\frac{\partial L}{\partial w_{11}^1}
=
\frac{\partial L}{\partial z} \frac{\partial z}{\partial b} \frac{\partial b}{\partial w_{11}^1}
=
\zeta \frac{\partial b}{\partial w_{11}^1}
\]
\( b = y_1 w_{11}^2 + y_2 w_{21}^2 \)であり、\( w_{11}^1 \)は\( y_2 \)に含まれないので、次式が得られます。
\[
\frac{\partial L}{\partial w_{11}^1}
=
\zeta \frac{\partial b}{\partial y_1} \frac{\partial y_1}{\partial a_1} \frac{\partial a_1}{\partial w_{11}^1}
=
\zeta w_{11}^2 \{ g(a_1) \}' x_1
\tag{4.4-8}
\]
\[
\left(
\frac{\partial y_1}{\partial a_1}
=
\frac{\partial g(a_1)}{\partial a_1}
=\{ g(a_1) \}'
\right)
\]
同様にして他の成分についても計算します。\[
\begin{eqnarray}
\frac{\partial L}{\partial w_{21}^1}
& = &
\zeta \frac{\partial b}{\partial y_1} \frac{\partial y_1}{\partial a_1} \frac{\partial a_1}{\partial w_{21}^1}
=
\zeta w_{21}^2 \{ g(a_1) \}' x_2
\\
\frac{\partial L}{\partial w_{12}^1}
& = &
\zeta \frac{\partial b}{\partial y_2} \frac{\partial y_2}{\partial a_2} \frac{\partial a_2}{\partial w_{12}^1}
=
\zeta w_{11}^2 \{ g(a_2) \}' x_1
\\
\frac{\partial L}{\partial w_{22}^1}
& = &
\zeta \frac{\partial b}{\partial y_2} \frac{\partial y_2}{\partial a_2} \frac{\partial a_2}{\partial w_{22}^1}
=
\zeta w_{21}^2 \{ g(a_2) \}' x_2
\end{eqnarray}
\]
以上を使って行列表現すると、次のようになります（偏微分の対角行列は（4.4-3）式を参照ください）。\[
\begin{eqnarray}
\frac{\partial L}{\partial W^1}
& = &
\zeta
\begin{pmatrix}
w_{11}^2 \{ g(a_1) \}' x_1 & w_{12}^2 \{ g(a_2) \}' x_1 &
\\
w_{21}^2 \{ g(a_1) \}' x_2 & w_{22}^2 \{ g(a_2) \}' x_2 &
\end{pmatrix}
\\
\\
& = &
\zeta
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
\left( w_{11}^2 \quad w_{21}^2 \right)
\begin{pmatrix}
\{ g(a_1) \}'& 0
\\
0 & \{ g(a_2) \}'
\end{pmatrix}
\\
\\
& = &
X^t \frac{\partial L}{\partial z} \{ h(b) \}' (W^2)^t \{ g(A) \}'
\tag{4.4-9}
\end{eqnarray}
\]
b）隠れ層を2層にしてみます。
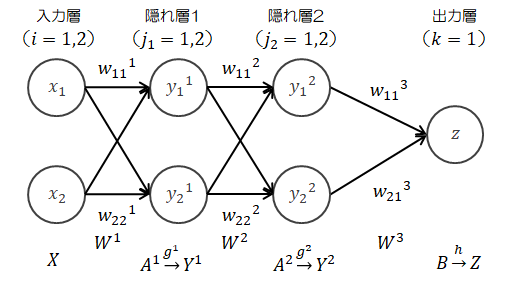このケースでは、\( \displaystyle \frac{\partial L}{\partial W^3} \)、\( \displaystyle \frac{\partial L}{\partial W^2} \)、\( \displaystyle \frac{\partial L}{\partial W^1} \)を求める必要があります。順伝播の計算は省略します。
\( \displaystyle \frac{\partial L}{\partial W^3} \)は（4.4-1）式の\( X \)を\( Y^2 \)に置き換えるだけです。
\[
\frac{\partial L}{\partial W^3}
=
(Y^2)^t \frac{\partial L}{\partial z} \{ h(b) \}'
\]
\( \displaystyle \frac{\partial L}{\partial W^2} \)は（4.4-9）式の\( X \)を\( Y^1 \)に、\( W^2 \)を\( W^3 \)に、\( g(A) \)を\( g^2(A^2) \)に置き換えるだけです。\[
\frac{\partial L}{\partial W^2}
=
(Y^1)^t \frac{\partial L}{\partial z} \{ h(b) \}' (W^3)^t \{ g^2(A^2) \}'
\]
\( \displaystyle \frac{\partial L}{\partial W^1} \)は成分計算した方がわかりやすいので、\( w_{11} \)に着目して計算してみます。\[
\frac{\partial L}{\partial w_{11}^1}
=
\frac{\partial L}{\partial z} \frac{\partial z}{\partial b} \frac{\partial b}{\partial w_{11}^1}
=
\zeta \frac{\partial b}{\partial w_{11}^1}
\]
隠れ層1で\( w_{11}^1 \)を含むのは\( a_1^1 \)、\( y_1^1 \)なので、これを見越して上式を変形します。\[
\frac{\partial L}{\partial w_{11}^1}
=
\zeta \frac{\partial b}{\partial y_1^1} \frac{\partial y_1^1}{\partial a_1^1} \frac{\partial a_1^1}{\partial w_{11}^1}
=
\zeta \frac{\partial b}{\partial y_1^1} \{ g^1(a_1^1) \}' x_1
\]
この式は（4.4-8）式と同じ形をしているので、その行列表現（4.4-9）式と照らし合わせて、次のように表すことができます。\[
\frac{\partial L}{\partial W^1}
=
X^t \zeta \frac{\partial b}{\partial Y^1} \{ g^1(A^1) \}'
\tag{4.4-10}
\]
ここで計算が残っている\( \displaystyle \frac{\partial b}{\partial Y^1} \)について見ていきます。成分計算した方がわかりやすいので、\( y_1^1 \)に着目して計算してみます。
\[
\begin{eqnarray}
\frac{\partial b}{\partial y_1^1}
& = &
\frac{\partial}{\partial y_1^1} ( y_1^2 w_{11}^3 + y_2^2 w_{21}^3 )
\\
& = &
w_{11}^3 \frac{\partial y_1^2}{\partial y_1^1}
+ w_{21}^3 \frac{\partial y_2^2}{\partial y_1^1}
\\
& = &
w_{11}^3 \frac{\partial y_1^2}{\partial a_1^2} \frac{\partial a_1^2}{\partial y_1^1}
+ w_{21}^3 \frac{\partial y_2^2}{\partial a_2^2} \frac{\partial a_2^2}{\partial y_1^1}
\\
& = &
w_{11}^3 \frac{\partial y_1^2}{\partial a_1^2} w_{11}^2
+ w_{21}^3 \frac{\partial y_2^2}{\partial a_2^2} w_{12}^2
\end{eqnarray}
\]
同様に\[
\frac{\partial b}{\partial y_2^1}
=
w_{11}^3 \frac{\partial y_1^2}{\partial a_1^2} w_{21}^2
+ w_{21}^3 \frac{\partial y_2^2}{\partial a_2^2} w_{22}^2
\]
以上より、\[
\begin{eqnarray}
\frac{\partial b}{\partial Y^1}
& = &
\left(
\frac{\partial b}{\partial y_1^1} \quad \frac{\partial b}{\partial y_2^1}
\right)
\\
& = &
(w_{11}^3 \quad w_{21}^3)
\begin{pmatrix}
\{ g^2(a_1^2) \}' & 0
\\
0 & \{ g^2(a_2^2) \}'
\end{pmatrix}
\begin{pmatrix}
w_{11}^2 & w_{12}^2
\\
w_{12}^2 & w_{22}^2
\end{pmatrix}
\\
& = &
(W^3)^t \{ g^2(A^2) \}' (W^2)^t
\end{eqnarray}
\tag{4.4-11}
\]
これを（4.4-10）式に代入して、\( \displaystyle \frac{\partial L}{\partial W^1} \)が求まります。\[
\frac{\partial L}{\partial W^1}
=
X^t \frac{\partial L}{\partial z} \{ h(b) \}' (W^3)^t \{ g^2(A^2) \}' (W^2)^t \{ g^1(A^1) \}'
\tag{4.4-12}
\]
\[
\left(
\zeta
=
\frac{\partial L}{\partial z} \{ h(b) \}'
\right)
\]
ここで、（4.4-1）式、（4.4-9）式、（4.4-12）式を比較してみます。
\[
\begin{eqnarray}
\frac{\partial L}{\partial W^1}
& = &
X^t \frac{\partial L}{\partial z} \{ h(b) \}'
\\
\frac{\partial L}{\partial W^1}
& = &
X^t \frac{\partial L}{\partial z} \{ h(b) \}' \txc{red}{(W^2)^t \{ g^1(A^1) \}'}
\\
\frac{\partial L}{\partial W^1}
& = &
X^t \frac{\partial L}{\partial z} \{ h(b) \}' \txc{red}{(W^3)^t \{ g^2(A^2) \}'} \txc{orange}{(W^2)^t \{ g^1(A^1) \}'}
\end{eqnarray}
\]
このように、隠れ層を追加していくごとに“重みと活性化関数の微分の積”\( (W^l)^t \{ g^{l-1}(A^{l-1}) \} \)が追加されます。
したがって、隠れ層を3層にしたときの\( \displaystyle \frac{\partial L}{\partial W^1} \)は
\[
\frac{\partial L}{\partial W^1}
=
X^t \frac{\partial L}{\partial z} \{ h(b) \}'
\txc{red}{(W^4)^t \{ g^3(A^3) \}'}
\txc{orange}{(W^3)^t \{ g^2(A^2) \}'}
\txc{blue}{(W^2)^t \{ g^1(A^1) \}'}
\]
となることが予想されます。c）隠れ層を3層にしてみます。
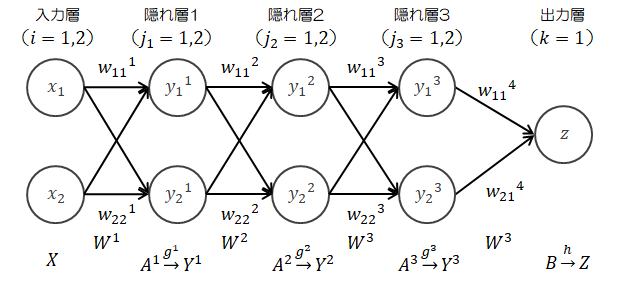このケースでは、\( \displaystyle \frac{\partial L}{\partial W^4} \)、\( \displaystyle \frac{\partial L}{\partial W^3} \)、\( \displaystyle \frac{\partial L}{\partial W^2} \)、\( \displaystyle \frac{\partial L}{\partial W^1} \)を求める必要があります。順伝播の計算は省略します。
\( \displaystyle \frac{\partial L}{\partial W^4} \)は（4.4-1）式を、\( \displaystyle \frac{\partial L}{\partial W^3} \)は（4.4-9）式を、\( \displaystyle \frac{\partial L}{\partial W^2} \)は（4.4-12）式を書き換えるだけです。
\[
\begin{eqnarray}
\frac{\partial L}{\partial W^4}
& = &
(Y^3)^t \frac{\partial L}{\partial z} \{ h(b) \}'
\\
\frac{\partial L}{\partial W^3}
& = &
(Y^2)^t \frac{\partial L}{\partial z} \{ h(b) \}' (W^4)^t \{ g^3(A^3) \}'
\\
\frac{\partial L}{\partial W^2}
& = &
(Y^1)^t \frac{\partial L}{\partial z} \{ h(b) \}' (W^4)^t \{ g^3(A^3) \}' (W^3)^t \{ g^2(A^2) \}'
\end{eqnarray}
\]
これまで同様\( \displaystyle \frac{\partial L}{\partial W^1} \)は計算する必要があります。
計算過程の詳細をここで紹介しても数式のお化けになってあまり本質的な意味はないので、pdfに記しておきます。
確認したい方はpdfをご覧ください。最終的に、\( \displaystyle \frac{\partial L}{\partial W^1} \)の計算結果は以下のとおりとなり、b）で予想した式と同じものになりました。
\[
\frac{\partial L}{\partial W^1}
=
X^t \frac{\partial L}{\partial z} \{ h(b) \}'
(W^4)^t \{ g^3(A^3) \}'
(W^3)^t \{ g^2(A^2) \}'
(W^2)^t \{ g^1(A^1) \}'
\tag{4.4-15}
\]
4．4．4．一般化する
ここまでの説明をあわせると損失関数の勾配を一般化できます。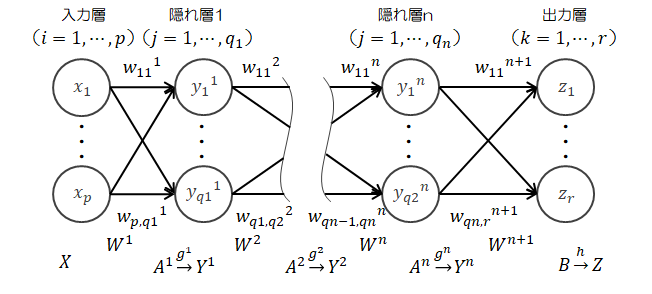
そこで隠れ層の層数を\( n \)とします。このとき、隠れ層\( m \)での損失関数の勾配は次式で表せます。\[
\begin{eqnarray}
\frac{\partial L}{\partial W^l}
& = &
(Y^{k-1})^t \frac{\partial L}{\partial Z} \{ h(B) \}'
\prod_{l=m}^n (W^{l+1})^t \{ g^l(A^l) \}'
\\
\\
& = &
(Y^{m-1})^t \frac{\partial L}{\partial Z} \{ h(B) \}'
(W^{n+1})^t \{ g^n(A^n) \}' \cdots (W^{m+1})^t \{ g^m(A^m) \}'
\end{eqnarray}
\tag{4.4-16}
\]
ただし、\( m=1 \)のとき\( Y^0=X \)
このように非常に簡単なパターンに従って、各層での損失関数の勾配を求めることができます。
ところで、損失関数は主に二乗和誤差と交差エントロピー誤差のどちらかを使用します。 それぞれの微分形は（4.2.1-1）式、（4.2.2-2）式で示したとおりです。
| 二乗和誤差 | ： | \( \displaystyle \frac{\partial L}{\partial z_k} = (t_k - z_k) \) |
| 交差エントロピー誤差 | ： | \( \displaystyle \frac{\partial L}{\partial z_k} = \displaystyle \frac{t_k}{z_k} \) |
| シグモイド関数 | ： | \( \displaystyle \frac{\partial y_j^l}{\partial a_j^l} = y_j^l (1 - y_j^l) \) |
| ソフトマックス関数 | ： |
従って、損失関数の勾配（4.4-4）式にこれらを代入しても、教師データ\( t_k \)、出力値\( z_k \)、隠れ層の出力値\( y_j^l \)の四則演算のみで求まります（下式は二乗和誤差の場合）。
\[
\frac{\partial L}{\partial W^l}
=
(Y^{l-1})^t \left\{ (t_k - z_k) y_j^l (1 - y_j^l) \right\}
\]
このようにして損失関数の勾配を求め、次式にもとづき各重みを修正できます。\[
\tilde{W^l}
=
W^l - \eta \frac{\partial L}{\partial W^l}
\tag{4.4-17}
\]
4．4．5．誤差逆伝播法の手順
最後に、ニューラルネットワークによる“重み”の調整手順をまとめます。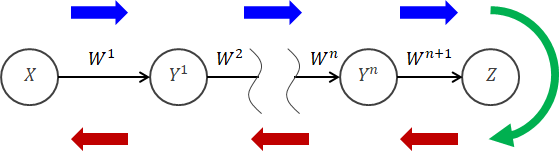
まずは順伝播の手順についてです（上図の青矢印で示した範囲）。
- すべての重み\( W^l \)(\(l=1,\cdots,k+1 \))の初期値をランダムかつ小さな値に設定します。 さらに、学習率\( \eta ( 0 \lt \eta \leq 1 ) \)を適当に設定します（目安：0.001～0.01程度）。
- 入力層に送られたデータ\( X \)に重み\( W^1 \)を掛け、隠れ層1に送ります。
- 隠れ層1の各ニューロンでは、送られてきた重み付きデータの総和をとり（\( A=XW^1 \)）、それに活性化関数が作用させて\( Y^1 \)を出力します。
- 出力\( Y^1 \)に重み\( W^2 \)を掛け、隠れ層2に送ります。
- 隠れ層2で（3）と同じ操作が行われ、\( Y^2 \)を出力します。
- 残りの隠れ層で（4）（5）と同じ操作が繰り返されます。
- 最後の隠れ層の出力\( Y^n \)に\( W^{n+1} \)を掛け、出力層に送られます。
- 出力層でも（3）と同じ操作が行われ、\( Z \)を出力します。
- 出力\( Z \)と教師データ\( T \)を使って損失を計算します。 損失関数に二乗和誤差を使う場合は差分を、交差エントロピー誤差の場合は比率（の対数）を使います。
- 損失関数の勾配\( \partial L / \partial W^{n+1} \)を計算し、それに学習率\( \eta \)入力データ\( X \)をかけたものを使って\( W^{n+1} \)を修正します。
\[ \tilde{W^l} = W^l - \eta \frac{\partial L}{\partial W^l} \] - （10）の操作を\( W^n \leftarrow \cdots \leftarrow W^2 \leftarrow W^1 \)まで繰り返します。
- 修正した重みを使って、（2）～（9）の手順で損失を計算します。 損失がある値（0に限りなく近い微小値：1e-4など）以下なら重みの調整は完了です。 そうでなければ（10）～（11）の操作を行い、損失の再評価を行います。
