ニューラルネットワーク
3．3．ニューラルネットワークの計算
ニューラルネットワークの計算は、実は非常に単純な行列計算で構成されています （添え字が多いので見づらいですが）。 本節ではその点について確認します。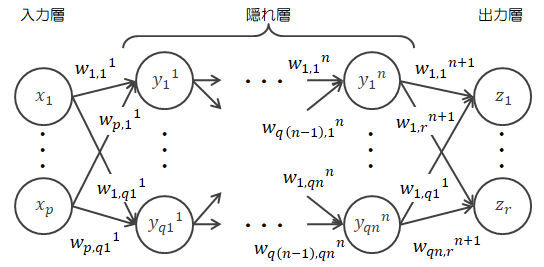
各データや重み活性化関数等の表記は3.1節の行列表示と同様とします。| 入力 | ： | \( X \in R^{1 \times p} \) |
| 重み | ： | \( W^l \in R^{q(l-1) \times ql} \) \((l=1,\cdots,n,n+1)\) |
| 重み付き総和 | ： | \( A^l \in R^{1 \times ql} \) \((l=1,\cdots,n,n+1)\) |
| 隠れ層の出力 | ： | \( Y^l \in R^{1 \times ql} \) \((l=1,\cdots,n)\) |
| 隠れ層の活性化関数 | ： | \( g_l(t) \) \((l=1,\cdots,n)\) |
| 出力層の活性化関数 | ： | \( h(t) \) |
| 出力 | ： | \( Z \in R^{1 \times r} \) |
| 隠れ層の層順 | ： | \( l \quad (l=1,\cdots,n) \) |
| 入力のニューロンの順番 | ： | \( i \quad (l=1,\cdots,p) \) |
| 隠れ層のニューロンの順番 | ： | \( j \quad (l=1,\cdots,q_l) \) |
| 出力層のニューロンの順番 | ： | \( k \quad (l=1,\cdots,r) \) |
|
なお、\(l=0 \rightarrow q_0=p\)、 \( l=n+1 \rightarrow q_{n+1}=r \)とします |
||
- 入力層→隠れ層1
まずは隠れ層1の各ニューロンで、入力データの重み付き総和を計算します。
\[ A^1 = X W^1 \in R^{1 \times q1} \] - 隠れ層1の処理
重み付き総和\( A^1 \)は、活性化関数によって出力値\( Y^1 \)に変換されます。
\[ Y^1 = g_1(A^1) \in R^{1 \times q1} \] - 隠れ層1→隠れ層2
ここでの処理は（1）の処理と全く同じです。
\[ A^2 = Y^1 W^2 \in R^{1 \times q2} \] - 隠れ層1の処理
ここも（2）の処理と全く同じです。
\[ Y^2 = g_2( A^2 ) \in R^{1 \times q2} \] - 隠れ層内の繰り返し処理
（3）（4）を\( l=n \)になるまで繰り返します。 - 隠れ層2→出力層
- 出力層の処理
もはや説明不要と思いますが、ここでも（1）（2）と同じ処理を行います （出力層での総和はこれまでと合わせて\( B (=A^{n+1} ) \)とします）。\[ \begin{eqnarray} B & = & Y^n W^{n+1} \in R^{1 \times r} \\ Z & = & h(B) \in R^{1 \times r} \end{eqnarray} \]
| 入力層→隠れ層1 | ： | \( Y^1 = g_1(XW^1) \) |
| 隠れ層1→隠れ層2 | ： | \( Y^2 = g_2(Y^1W^2) \) |
| ・・・ | ||
| 隠れ層n-1→隠れ層n | ： | \( Y^n = g_n(Y^{n-1}W^n) \) |
| 隠れ層n→出力層 | ： | \( Z = h(Y^nW^{n+1}) \) |
ただ、これまでの計算は重みがわかっている前提になっていますが、ニューラルネットワークはこの重みを学習しながら決めていくことになります。
次章以降では、この重みの決め方について見ていくことにします。
