ニューラルネットワーク
4.4.誤差逆伝播法
3章までは主に、入力から出力が得られるまでの話をしてきました。 この計算過程を順伝播といいます(下図青線部分)。 それに対し“学習”の手順は、出力と教師データの誤差(下図緑線部分)を最小にするよう、順伝播とは逆の手順をたどって各重みを調整していきます。 この操作を逆伝播といいます(下図赤線部分)。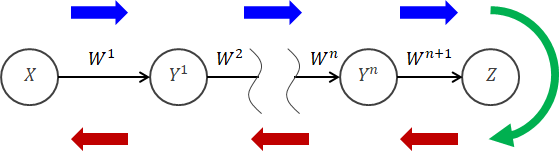 この逆伝播では誤差が各重みの調整に深く関与します。
この方法を誤差逆伝播法といい、ニューラルネットワークの学習で通常用いられます。
この逆伝播では誤差が各重みの調整に深く関与します。
この方法を誤差逆伝播法といい、ニューラルネットワークの学習で通常用いられます。手順だけを見れば2.3節で説明したパーセプトロンの学習とかなり似ていますが、ニューラルネットワークでは連続値を出力する非線形な活性化関数が組み込まれています。 そのため、損失関数の勾配は活性化関数の影響を受けます。
そこでまずは、各重みの調整に関与する損失関数の勾配の計算に着目して話を進めます。 前提として、活性化関数は微分可能とします。
なお話が進むにつれ、変数の添え字がたくさんついてきたり、数式が複雑になってわかりにくくなっていきますが、その中にはきちんとした法則性があるのでそれほど難しいものではありません (面倒ですけど...)。
4.4.1.最も簡単なネットワーク
入力層と出力層のネットワークについて計算してみます。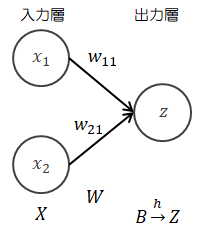
| 入力 | : | \( X = (x_1, x_2) \in R^{1 \times 2} \) |
| 重み | : | \( W = \begin{pmatrix} w_{11} \\ w_{21} \end{pmatrix} \in R^{2 \times 1} \) |
| 重み付き総和 | : | \( B=(b) \in R \)(スカラー) |
| 出力 | : | \( Z=h(B)=(h(b)) \in R \)(スカラー) |
| 入力層→出力層 | : | \( b = XW ( = x_1 w_{11} + x_2 w_{21} ) \) |
| 出力層の処理 | : | \( z = h(b) \) |
\[
\frac{\partial L}{\partial w_{11}}
=
\frac{\partial L}{\partial b} \frac{\partial b}{\partial w_{11}}
\]
とできるのは、\( \displaystyle \frac{1}{2} = \frac{1}{3} \frac{3}{2} \)とおなじことをしている、と思ってもらえば十分です。さらに計算を進めて次式を得ます。
\[
\frac{\partial L}{\partial w_{11}}
=
\frac{\partial L}{\partial z} \frac{\partial z}{\partial b} \frac{\partial b}{\partial w_{11}}
=
\frac{\partial L}{\partial z} \{ h(b) \}' x_1
\]
\[
\left(
\frac{\partial z}{\partial b}
=
\frac{\partial h(b)}{\partial b}
=
\{ h(b) \}'
\right)
\]
\(w_{21} \)も同じように計算して、\[
\frac{\partial L}{\partial w_{21}}
=
\frac{\partial L}{\partial z} \{ h(b) \}' x_2
\]
損失関数の勾配は次のようになります。\[
\begin{eqnarray}
\frac{\partial L}{\partial W}
& = &
\begin{pmatrix}
\displaystyle \frac{\partial L}{\partial w_{11}}
\\
\displaystyle \frac{\partial L}{\partial w_{21}}
\end{pmatrix}
\\
& = &
\frac{\partial L}{\partial z} \{ h(b) \}'
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
\\
& = &
X^t \frac{\partial L}{\partial z} \{ h(b) \}'
\end{eqnarray}
\tag{4.4-1}
\]
\( X^t \)は\(X\)の転置行列(行と列をいれかえたもの)です。
\( \displaystyle \frac{\partial L}{\partial z} \{ h(b) \}' \)はスカラーです。
厳密にいえば\( X^t \in R^{2 \times 1} \)、\( \{ h(b) \}' \in R^{1 \times 1} \)ですので、(4.4-1)式の\( X^t \)を後ろにすると\( R^{1 \times 1} \times R^{2 \times 1} \) となって不都合があるので、\( X^t \)を前に表記しています。この行列表現の式は、入力層のニューロンの数を増やしても\( X \)の次元が変わるだけで何も変わりません。
4.4.2.出力層のニューロンを増やす
出力層のニューロンの数を増やしてみます。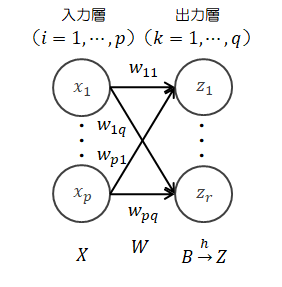
| 入力 | : | \( X = (x_1, \cdots, x_p) \in R^{1 \times p} \) |
| 重み | : | \( W = \begin{pmatrix} w_{11} & \cdots & w_{1q} \\ \vdots & \ddots & \vdots \\ w_{p1} & \cdots & w_{pq} \end{pmatrix} \in R^{p \times q} \) |
| 重み付き総和 | : | \( B=(b_1, \cdots, b_r) \in R^{1 \times r} \) |
| 出力 | : | \( Z=h(B) \in R^{1 \times r} \) |
| 入力層→出力層 | : | \( b = XW = ( x_1 w_{11} + x_2 w_{21}, \quad x_1 w_{12} + x_2 w_{22} ) \) |
| 出力層の処理 | : | \( Z = h(B) = (h(b_1), h(b_2)) \) |
\[
\frac{\partial L}{\partial W}
=
\left( \frac{\partial L}{\partial w_{ik}} \right)
=
\left( \frac{\partial L}{\partial z_k}
\frac{\partial z_k}{\partial b_k}
\frac{\partial b_k}{\partial w_{ik}}
\right)
\in R^{p \times r}
\]
\( \displaystyle \frac{\partial b_k}{\partial w_{ik}} \)は簡単に計算できるので、
\[
\begin{eqnarray}
\frac{\partial b_k}{\partial w_{ik}}
& = &
\frac{\partial \displaystyle \sum_{s=1}^p x_s w_{sk}}{\partial w_{ik}}
\\
& = &
\frac{\partial ( x_1 w_{1k} + \cdots + x_i w_{ik} + \cdots + x_p w_{pk} )}{\partial w_{ik}}
\\
& = &
x_i
\end{eqnarray}
\]
損失関数の勾配は次のように書き換えられます。\[
\begin{eqnarray}
\frac{\partial L}{\partial W}
& = &
\left(
\frac{\partial L}{\partial z_k} \frac{\partial z_k}{\partial b_k} x_i
\right)
\\
\\
& = &
\begin{pmatrix}
\displaystyle \frac{\partial L}{\partial z_1} \frac{\partial z_1}{\partial b_1} x_1 & \cdots & \displaystyle \frac{\partial L}{\partial z_r} \frac{\partial z_r}{\partial b_r} x_1
\\
\vdots & \cdots & \vdots
\\
\displaystyle \frac{\partial L}{\partial z_1} \frac{\partial z_1}{\partial b_1} x_p & \cdots & \displaystyle \frac{\partial L}{\partial z_r} \frac{\partial z_r}{\partial b_r} x_p
\end{pmatrix}
\\
\\
& = &
\begin{pmatrix}
x_1
\\
\vdots
\\
x_p
\end{pmatrix}
\left(
\frac{\partial L}{\partial z_1} \frac{\partial z_1}{\partial b_1}
\quad \cdots \quad
\frac{\partial L}{\partial z_r} \frac{\partial z_r}{\partial b_r}
\right)
\end{eqnarray}
\tag{4.4-2}
\]
ここで\( \displaystyle \frac{\partial L}{\partial z_k} \)を行列表現すると、次のようになります。\[
\left( \frac{\partial L}{\partial z_k} \right)
=
\left(
\frac{\partial L}{\partial z_1}
\quad \cdots \quad
\frac{\partial L}{\partial z_r}
\right)
=
\frac{\partial L}{\partial Z}
\in R^{1 \times r}
\tag{4.4-3}
\]
また\( \)を行列表現すると、次のようになります。\[
\left( \frac{\partial z_k}{\partial b_k} \right)
=
\left( \delta_{sk} \frac{\partial z_s}{\partial b_k} \right)
=
\begin{pmatrix}
\displaystyle \frac{\partial z_1}{\partial b_1} & & O
\\
& \ddots &
\\
O & & \displaystyle \frac{\partial z_r}{\partial b_r}
\end{pmatrix}
=
\frac{\partial Z}{\partial B}
\in R^{r \times r}
\tag{4.4-4}
\]
この式に含まれる\( \delta_{sk} \)はデルタ関数といい、次のように定義されます。\[
\begin{eqnarray}
\delta_{sk}
=
\begin{cases}
1 & (s=k)
\\
0 & (s \neq k)
\end{cases}
\end{eqnarray}
\]
ここで次の計算を行います。\[
\begin{eqnarray}
\frac{\partial L}{\partial Z} \frac{\partial Z}{\partial B}
& = &
\left( \frac{\partial L}{\partial z_1} \quad \cdots \quad \frac{\partial L}{\partial z_r} \right)
\begin{pmatrix}
\displaystyle \frac{\partial z_1}{\partial b_1} & & O
\\
& \ddots &
\\
O & & \displaystyle \frac{\partial z_r}{\partial b_r}
\end{pmatrix}
\\
\\
& = &
\left( \frac{\partial L}{\partial z_1} \frac{\partial z_1}{\partial b_1} \quad \cdots \quad \frac{\partial L}{\partial z_r} \frac{\partial z_r}{\partial b_r} \right)
\in R^{1 \times r}
\tag{4.4-6}
\end{eqnarray}
\]
(4.4-6)式は(4.4-2)式に含まれるので、損失関数の勾配は次のように書き換えられます。\[
\frac{\partial L}{\partial W}
=
X^t \frac{\partial L}{\partial Z} \frac{\partial Z}{\partial B}
\tag{4.4-7}
\]
さらに、a)でみたように、活性化関数の重み付き総和による微分は\( \displaystyle \frac{\partial Z}{\partial B} = \{ h(B) \}' \) 、各成分 \( \displaystyle \frac{\partial z_k}{\partial b_k} = \{ h(b_k) \}' \)
で表せるので、(4.4-7)式は次のように書き換えられます。\[
\frac{\partial L}{\partial W}
=
X^t \frac{\partial L}{\partial Z} \{ h(B) \}'
\tag{4.4-8}
\]
また、(4.4-4)式は次のように書き換えられます。\[
\frac{\partial Z}{\partial B}
=
\begin{pmatrix}
\displaystyle \frac{\partial z_1}{\partial b_1} & & O
\\
& \ddots &
\\
O & & \displaystyle \frac{\partial z_r}{\partial b_r}
\end{pmatrix}
=
\begin{pmatrix}
\{ h(b_1) \}' & & O
\\
& \ddots &
\\
O & & \{ h(b_r) \}' \quad
\end{pmatrix}
=
\{ h(B) \}'
\]


