ニューラルネットワーク
3．ニューラルネットワークの仕組み
3．1．ニューラルネットワークの仕組み
2.2節のANDやOR等のパーセプトロンは、その“重み”を人が適当に決めていました。 つまり判別について大事なところは人手に頼っている、ということです。 これでは機械学習とは言えません。 また、単純パーセプトロンであれば機械学習は可能でしたが、XORのような線形分離できないものには適用できませんでした。人は産まれてから成長していくにしたがって、学習を何度も繰り返して予測や判別がつくようになります。 また、ANDやORだけでなくXORについても理解できます。 これと同じように、「コンピュータもデータから自動で学習し、予測や判別を行うようなアルゴリズムを実装する」のが機械学習の狙いです。 それを実現するには、コンピュータが学習によって“重み”を自動で設定しなければなりません。 ニューラルネットワークの重要な性質は「適切な重みを自動で学習できる」ことにあります。
本節ではニューラルネットワークの学習に入る前に、その仕組みについて説明していきます。
ニューラルネットワークは次のような構造を持ちます。
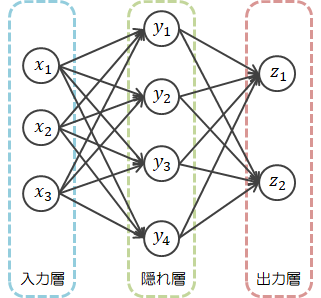図は隠れ層を1層としていますが、複数の層で構成される方が一般的です。さて、上図にもとづくニューラルネットワークのデータの流れは次のとおりです。
このとき、入力データ、重み、隠れ層の出力、出力データをそれぞれ行列で表すと、次のようになります。
\[
\begin{eqnarray}
X
& = &
(x_1, x_2, x_3)
=
(x_i) \quad (i=1,2,3)
\\
Y
& = &
(y_1, y_2, y_3, y_4)
=
(y_j) \quad (j=1,2,3,4)
\\
Z
& = &
(z_1, z_2)
=
(z_k) \quad (k=1,2)
\\
\\
W^1
& = &
\begin{pmatrix}
w_{11}^1 & w_{12}^1 & w_{13}^1 & w_{14}^1
\\
w_{21}^1 & w_{22}^1 & w_{23}^1 & w_{24}^1
\\
w_{31}^1 & w_{32}^1 & w_{33}^1 & w_{34}^1
\end{pmatrix}
=
(w_{ij}^1)
\\
\\
W^2
& = &
\begin{pmatrix}
w_{11}^2 & w_{12}^2
\\
w_{21}^2 & w_{22}^2
\\
w_{31}^2 & w_{32}^2
\\
w_{41}^2 & w_{42}^2
\end{pmatrix}
=
(w_{jk}^2)
\end{eqnarray}
\]
重み\( w_{ij}^1 \)の添え字については次の規則に従います。
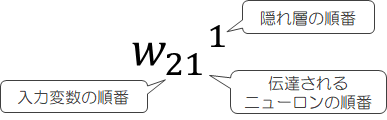
- 入力層に届いたデータ\( X \)は、パーセプトロンと同様に重み\( W^1 \)が掛けられ、隠れ層に伝わります。
- 隠れ層の各ニューロンでそれらの総和\( a_j^1 \)をとり、それを変数とする関数\( g(a_j^1) \)の値を\( y_j \)として出力します。
ちなみに、パーセプトロンの関数\( g(a) \)はステップ関数でした。
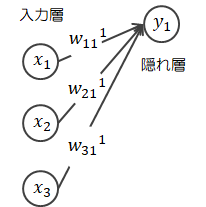隠れ層>ニューロン1の出力：
\[ a_1^1 = x_1 w_{11}^1 + x_2 w_{21}^1 + x_3 w_{31}^1 \rightarrow g(a_1) = y_1 \]隠れ層を一括出力：\[ A^1 = XW^1 \rightarrow g(A^1) = Y \] - 隠れ層の出力\( Y \)に重み\( W^2 \)が掛けられ、出力層に伝わります。
- 隠れ層のとき同様、それらの総和\( b \)をとり、それを変数とする関数\( h(b) \)の値を\( z_k \)として出力します。
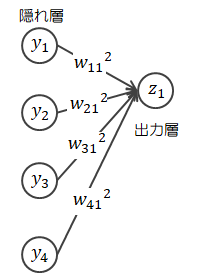出力層>ニューロン1の出力：
\[ b_1 = y_1 w_{11}^2 + y_2 w_{21}^2 + y_3 w_{31}^2 + y_4 w_{41}^2 \rightarrow g(b_1) = z_1 \]出力層を一括出力：\[ B = YW^2 \rightarrow g(B) = Z \]
3．2．活性化関数
前節では、隠れ層や出力層で用いた関数\( g(a), h(b) \)の説明には特に触れませんでしたので、ここで説明します。ニューラルネットワークにおいて、入力信号の和を出力信号に変換する関数のことを活性化関数と呼びます （先ほどの\( g(a), h(b) \)がこれに該当します）。 活性化関数はニューロンの発火のように「入力信号の和がどのようにして活性化するか」を決定するものです。 ちなみに、パーセプトロンで用いたステップ関数も活性化関数の一つですが、ここでは区別します。
ニューラルネットワークで主に用いられる活性化関数について説明します。
3．2．1．隠れ層の活性化関数
この節では、隠れ層で使用する活性化関数について説明します。（1）シグモイド関数
シグモイド関数は次式で定義され、グラフ化すると下図のようになります。\[
f(x)
=
\frac{1}{1+\exp (-x)}
\tag{3.2.1-1}
\]
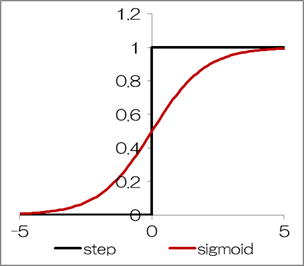シグモイド関数の特徴は「なめらかなで微分可能な曲線である」ということです。この特徴が、後述する“誤差逆伝播による学習”（4.4節）にとって重要な役割を持ちます。 ステップ関数は微分可能でないため、この点が大きな違いとなります。
シグモイド関数を微分すると次のようになります。
\( t=\exp(-x) \)、\( y=1/(1+t) \)とおいて
\[
\begin{eqnarray}
\frac{dy}{dx}
& = &
\frac{dy}{dt} \frac{dt}{dx}
\\
& = &
\frac{-1}{(1+t)^2 \quad} \{ -\exp(x) \}
\\
& = &
\frac{1}{1+t} \frac{t}{1+t}
\\
& = &
\frac{1}{1+t} \frac{(1+t)-t}{1+t}
\\
& = &
y(1-y)
\end{eqnarray}
\tag{3.2.1-2}
\]
このようにシグモイド関数の微分は、出力のみで簡単に計算できるのが大きなメリットになります。（2）ReLU関数
ReLU関数（Rectified Linear Unit）は次式で表し、グラフ化すると下図のようになります。\[
f(x)
=
\max ( 0, x )
\tag{3.2.1-3}
\]
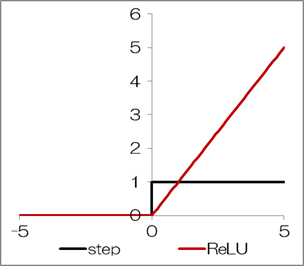ReLU関数は\( x=0 \)で微分不能で、\( x \lt 0 \)で勾配は0になりますが、シグモイド関数で生じる問題（勾配消失）が起こりにくく、性能が良いとされています。
3．2．2．出力層の活性化関数
この節では、出力層で使用する活性化関数について説明します。（1）恒等関数
恒等関数は入力をそのまま出力します（\( y_i=x_i \)）。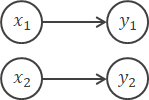
（2）ReLU関数
ソフトマックス関数は次式で表します。\[
f(x)
=
\frac{ \exp (x_k) }{ \sum \exp (x_i) }
\tag{3.2.2-1}
\]
出力層の前にある隠れ層の全出力\( x_i (1,\cdots,n) \)をすべて指数関数化\( \exp (x_i) \)し、\( k \)番目の出力\( \exp (x_k) \)を全合計で割ったものになります。
従って出力は0～1の値をとり、その総和は1になります（正規化）。
この特徴にプラス、ソフトマックス関数では入力の大小の順位は変わりませんので、各出力層の値を確率として解釈できます。
ニューラルネットワークが対象とする問題について、分類はソフトマックス関数を、回帰は恒等関数を出力関数として使用するのが一般的です。ソフトマックス関数を微分すると次のようになります。
- \( j= k \)のとき
\[ \begin{eqnarray} \frac{dy_k}{dx_k} & = & \frac{1}{\sum \exp(x_i)} \frac{d(\exp(x_k))}{dx_k} + \exp(x_k) \frac{d}{dx_k} \left( \frac{1}{\sum \exp(x_i)} \quad \right) \\ \\ & = & \frac{\exp(x_k)}{\sum \exp(x_i)} + \exp(x_k) \left\{ \frac{-\exp(x_k)}{(\sum \exp(x_i))^2} \quad \right\} \\ \\ & = & \frac{\exp(x_k)}{\sum \exp(x_i)} \quad \left( 1 - \frac{\exp(x_k)}{\sum \exp(x_i)} \quad \right) \\ \\ & = & y_k(1-y_k) \end{eqnarray} \]
- \( j\neq k \)のとき
\[ \begin{eqnarray} \frac{dy_k}{dx_j} & = & \exp(x_k) \frac{d}{dx_j} \left( \frac{1}{\sum \exp(x_i)} \quad \right) \\ \\ & = & \exp(x_k) \left\{ \frac{-\exp(x_j)}{(\sum \exp(x_i))^2} \quad \right\} \\ \\ & = & -\frac{\exp(x_k)}{\sum \exp(x_i)} \quad \frac{\exp(x_j)}{\sum \exp(x_i)} \\ \\ & = & -y_k y_j \end{eqnarray} \]
\[
\frac{dy_k}{dx_j}
=
\begin{cases}
y_k (1 - y_k) & (i=k) &
\\
-y_k y_j & (i \neq k) &
\end{cases}
\tag{3.2.2-2}
\]
3．2．3．活性化関数が非線形関数である理由
ニューラルネットワークでは、活性化関数に連続値をとる非線形な関数を使います。 理由は次の通りです。活性化関数に線形関数を用いるとします。 入力\( x \)、線形関数\( f(x)=cx \)としてネットワークを構築すると、出力\( y \)は\( y=f(f(f(x)))=cccx \)になります。 これは単に\( a=c^3 \)とした単層の隠れ層\( f(x)=ax \)と違いありません。 つまり、線形な活性化関数を多層にしたところで何らメリットは生じ、線形分離できない問題には適用できません
隠れ層を多層にするメリットを得るためには、活性化関数に連続かつ非線形な関数を用いなければなりません。
