ニューラルネットワーク
2．パーセプトロン
2．1．パーセプトロン
前章でみたニューロンの挙動をまとめると、次のようになります。- 多数の他のニューロンから信号（電流）が送られる
- シナプスの結合効率に応じて信号を受け取る
- 受け取った信号に応じて膜電位が決まる
- 膜電位が閾値を超えると信号を出力し、越えなければ何もしない
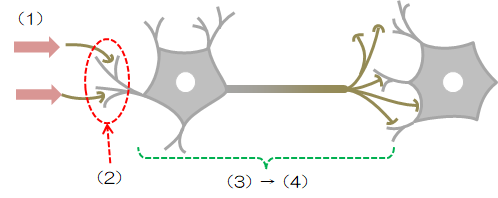この挙動を模擬した数理モデルをパーセプトロンといいます（人工ニューロンともいいます）。パーセプトロンはニューロンそのものを模擬するというより、ニューロンの概念を踏襲した上で極力簡潔な数式でモデル化したものです。
そこで、ニューロンの挙動をもとにパーセプトロンのモデル化を行ってみます。
- 入力信号に相当するデータを\( x_k \)とします
- シナプスの結合効率に相当する重み（係数）を\( w_k \)とします
- 膜電位に相当するものとして、入力信号の重み付き和\( a \)を算出します
\[ a = \sum_{k=1}^n x_k w_k \tag{2.1-1} \] - この総和\( a \)が閾値\( \theta \)を超えれば\( y=1 \)、それ以外のときは\( y=0 \)を出力します
\[ \begin{eqnarray} y = \begin{cases} 1 & ( a \gt \theta ) \\ 0 & ( a \leq \theta ) \end{cases} \end{eqnarray} \tag{2.1-2} \]
ここで（2.1-1）式に対して一工夫入れます。
\[
a'
=
\sum_{k=1}^n w_k x_k - \theta
\]
とし、さらに\( k=0 \)のとき\( x_0=1 \)、\( w_0 = -\theta \)とすれば式を簡略化できます（\( k=0 \)になります）。\[
a'
=
\sum_{k=0}^n w_k x_k
\]
これを（2.1-2）式にあてはめれば、次の関係式に書き換えられます。
\[
y
=
\begin{cases}
1 & ( a' \gt 0 )
\\
0 & ( a' \leq 0 )
\end{cases}
\tag{2.3-1}
\]
なお、（2.3-1）の条件式はステップ関数といい、グラフ化すると次のようなものになります。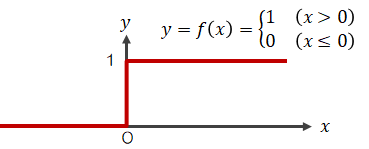
以上の内容を図式化します。ニューロンでは、重み付き総和\( a \)にステップ関数の処理を施したものを\( y \)として出力するので、ニューロンの中身を省略せずに書けば次のようになります。
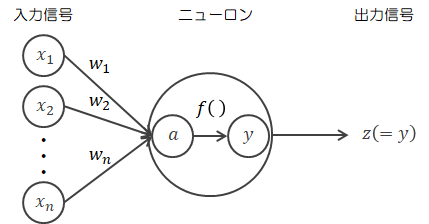さて、ここで先のことを考えて行列による表現を導入します。そのための準備として次のことを確認しておきます。
- 行列のサイズ
行列のサイズは行数×列数で表します。例えば、次のようなかんじです（Rについている2が行数、3が列数）。
\[ W = \begin{pmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \end{pmatrix} \in R^{2 \times 3} \] - 行列の略記
行列は次のように簡略表示できます（\( i \)：行番号、\( j \)：列番号）。
\[ W = ( w_{ij} ) \quad (1 \leq i \leq m, 1 \leq j \leq n ) \] - 行列の転置
行列𝑊の行と列を入れ替える操作を転置といい、入れ替えた行列を転置行列といい、\( W^t \)で表します。
\[ W = \begin{pmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \end{pmatrix} = ( w_{ij} ) \in R^{2 \times 3} \\ \downarrow \\ W^t = \begin{pmatrix} w_{11} & w_{21} \\ w_{12} & w_{22} \\ w_{13} & w_{23} \end{pmatrix} = ( w_{ji} ) \in R^{3 \times 2} \] - 行列の積
ここで、行列計算のルールについて確認しておきます。
行列AとBの積A×Bは、Aの列数とBの行数が一致しなければなりません。 また、A×Bの結果Cは、Cの行数=Aの行数、Cの列数=Bの列数になります。 例えば、\( A \in R^{2×3}、B \in R^{3×2} \)とすれば、\( C \in R^{2×2} \)となります。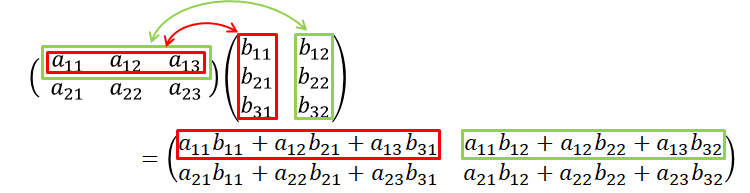
\[
X
=
(x_0, x_1, \cdots , x_n)
\in
R^{1 \times n}
,
\quad
W
=
\begin{pmatrix}
w_0
\\
w_1
\\
\vdots
\\
w_n
\end{pmatrix}
\in
R^{n \times 1}
\]
（\(x_0 = 1, w_0 = -\theta \)はお忘れなく）
とすることで、重みの総和は行列の積で表せるようになります。
\[
a'
=
XW
\tag{2.1-4}
\]
（ \( R^{1 \times n} \times R^{n \times 1} = R^{1 \times 1} \)、つまり\(a'\)はスカラー）
この表現において、閾値\( \theta \)に関する項は単純に定数分総和をずらすものなのでバイアス項といいます。 バイアス項はすでに重みに含まれているので、今後はバイアス項も重みとして扱います。
ここまでで見たパーセプトロンは非常に単純なもので、単純パーセプトロンといいます。 また、このパーセプトロンを使って複数の層を構成したものを多層パーセプトロンといいます。
