ニューラルネットワーク
2.2.論理回路
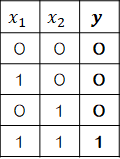
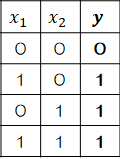
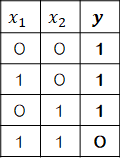
ここで単純パーセプトロンを使って、簡単な論理回路を作ってみます。| AND | OR | NAND |
|---|---|---|
 |
 |
 |
| AND | OR | NAND | |
|---|---|---|---|
| \( w_1 \) | 1 | 1 | -1 |
| \( w_2 \) | 1 | 1 | -1 |
| \( b \) | -1.4 | -0.5 | 1.4 |
| \( (0,0) \) | 0 \( ( y=-1.4 ) \) |
0 \( ( y=-0.5 ) \) |
1 \( ( y=-1.4 ) \) |
| \( (0,1) \) | 0 \( ( y=-0.4 ) \) |
1 \( ( y=0.5 ) \) |
1 \( ( y=0.4 ) \) |
| \( (1,0) \) | 0 \( ( y=-0.4 ) \) |
1 \( ( y=-0.5 ) \) |
1 \( ( y=0.4 ) \) |
| \( (1,1) \) | 1 \( ( y=0.64 ) \) |
1 \( ( y=-1.5 ) \) |
0 \( ( y=-0.6 ) \) |
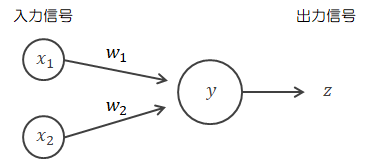
\[
\begin{eqnarray}
y
=
x_1 + x_ 2 +b
\rightarrow
z
=
\begin{cases}
1 \quad ( y \gt \theta )
\\
0 \quad ( y \leq \theta )
\end{cases}
\end{eqnarray}
\tag{2.2-1}
\]
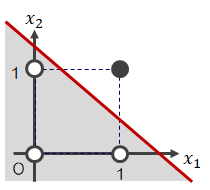
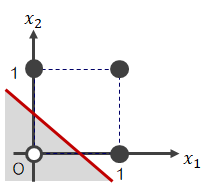
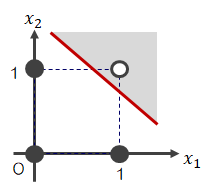
これらをグラフ化すると、次のように表せます。なお、●=1、◯=0です。| AND | OR | NAND |
|---|---|---|
 |
 |
 |
では、次のような状態はどうでしょう?
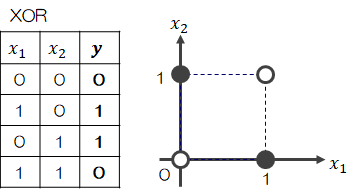 XORは排他的論理和という論理回路です。
この場合、グラフ上どうやっても◯と●を1本の直線だけで区分けできず、曲線(線形でない=非線形)になってしまいます。
XORは排他的論理和という論理回路です。
この場合、グラフ上どうやっても◯と●を1本の直線だけで区分けできず、曲線(線形でない=非線形)になってしまいます。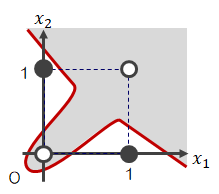 単純パーセプトロンは直線(2.1-3)や(2.2-1)式によって表現されているので、非線形な分離はできません。
単純パーセプトロンは直線(2.1-3)や(2.2-1)式によって表現されているので、非線形な分離はできません。ところが、AND、OR、NANDを組み合わせることでXORは表現可能となります。
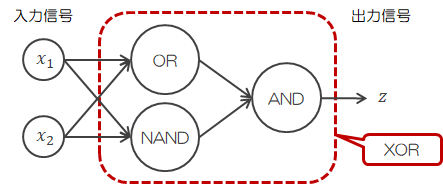
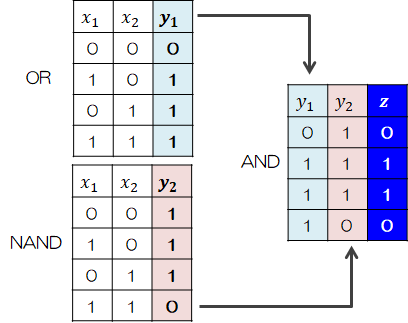 このように、XORは第1層にORとNAND、第2層にANDを設けた多層パーセプトロンになります。
このように、XORは第1層にORとNAND、第2層にANDを設けた多層パーセプトロンになります。このように、単純パーセプトロンだけでは表現できなかったこと(非線形な区分)が、複数のパーセプトロンで層を重ねることで表現可能となります。
2.3.パーセプトロンの学習
前節の論理回路では重みをユーザーが適当に決めました。 それでは今までの方法と何ら変わりません。 機械学習の目的は、自動でデータから学習して最適な出力を出すことにあります。 そのために機械学習で行うことは、データを使って自動で重みを調整することです。 そこでまずは、単純パーセプトロンで行える学習について説明します。単純パーセプトロンは、“誤り訂正学習法”という手法を使って自動で重みを決定できます。 誤り訂正学習法は“教師あり学習”の1つの手法で、「入力信号に対して正解ラベル(教師信号)が与えられるとき、教師信号と出力信号が一致するまで重みを修正し続ける」ものです。 本節では、この誤り訂正学習法について説明していきます。 なお、2.1節に従って入力信号を\( X \in R^{1 \times n} \)、重みを\( W \in R^{n \times 1} \)として扱います。
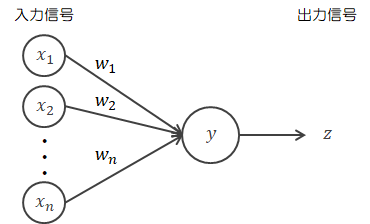 \( (x_1,x_2,\cdots, x_n) \)を1つの組とする入力パターン信号\( X_i \)( \(i = 1, 2, \cdots, p \))に対して、正解ラベル\( t_i \)が貼られているとします。
イメージとしては、p個の手書きの数字にそれぞれコンピュータが認識できる数字のラベルが貼られていて、1個ずつパーセプトロンで処理していく、といった感じです。
\( (x_1,x_2,\cdots, x_n) \)を1つの組とする入力パターン信号\( X_i \)( \(i = 1, 2, \cdots, p \))に対して、正解ラベル\( t_i \)が貼られているとします。
イメージとしては、p個の手書きの数字にそれぞれコンピュータが認識できる数字のラベルが貼られていて、1個ずつパーセプトロンで処理していく、といった感じです。
- 重み\( W \)の初期値をランダムかつ小さな値で設定します。さらに学習率\( \eta ( 0 \lt \eta \leq 1) \)を設定します。
- \( p \)個の入力パターンの中から1つ\( X_i \)を選び、パーセプトロンの入力層に与えます。
- ニューロンで次式の処理を行います。
\[ \begin{eqnarray} a_i = X_i W \rightarrow y_i = \begin{cases} 1 \quad ( a_i \gt 0) \\ 0 \quad (a_i \leq 0 ) \end{cases} \end{eqnarray} \](\( z = y \)は省略します)
- 「教師信号\( t_i \)と出力信号\( y_i \)の差分」と入力信号\( X_i \)を使って重み\( W \)を修正します
(修正済みの重みを\( \tilde{W} \)とします)。
\[ \tilde{W} = W + \eta ( t_i - y_i ) X_i \tag{2.3-1} \] - \( p \)個の入力パターンすべてに対して(2)~(4)の処理を行います。 このとき、が変化しなくなれば重み\( W \)の修正は完了です。 そうでなければ再度(2)~(4)を繰り返します。
ところが、2.2節でみたXORのようなパーセプトロン(非線形なもの)を含むと誤り修正学習法では対応できなくなります。 この問題については、4章の誤差逆伝播で説明します。


