回帰分析については、WebアプリとExcelツールをフリーで公開していますので、そちらもご活用ください。
1．回帰分析
回帰とは、データに内在する規則性あるいは法則性を“統計学”に基づいてモデル化 = 関数化することで、それによって得られた関数を回帰モデルと呼びます。回帰モデルは、現象の要因となる変数 =“説明変数”と、結果を表す変数 =“目的変数”によって表します。
例えば、ばねにおもりを吊るしたときのばねの伸び量を測定したとき、次のようなグラフが得られます。
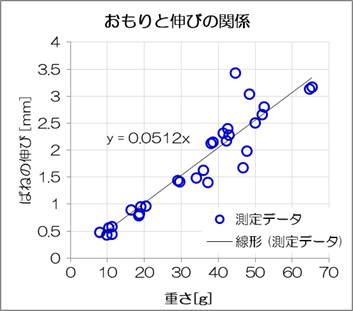
図1－1 回帰分析の例
グラフから説明変数と目的変数の間には、おおむね比例関係が得られています。ばねの伸び量は、ばねに加わる力と比例の関係（フックの法則）にあるので、この関係は妥当であると判断できます。また、グラフ上で得られた線形関数\( y=0.0512x \)は回帰モデルであり、係数0.0512はばね定数に相当します。ばね定数がわかれば、例えば重さ25gのものを吊るせばばねの伸びは1.3mmとなることが予測できます。
このように、回帰分析は「現象の把握や予測モデルの構築」に非常に有用な手法です。
例では単純な二変数の比例関係を取り上げましたが、非線形でも、複数の変数でもモデル化できます。
例えば、 \( y = e^{-ax}+x \)（非線形）、 \( y=c_n x_n + \cdots + c_1 x_1 + c_0 \)（多変数）
回帰モデルの決め方については主に次のものが挙げられます。- 最小二乗法（Least Squares Method）
- 最尤推定法（Maximum Likelihood Estimation）
2．最小二乗法
最小二乗法（Least Squares Method）とは、各データの測定誤差の二乗和が最小となるよう回帰モデル（関数）の係数を決定する方法です。最小二乗法は次の前提条件に基づき決定されます。
- 測定誤差（残差）は正規分布に従い、その平均値は0になります。
- 各測定パラメータは互いに独立です。
2．1．二変数の回帰分析
2．1．1．二変数の線形回帰
まずは最も簡単な、最小二乗法による二変数の線形回帰について説明します。 そこで、ばねにつるしたおもりの重さとばねの伸び量の例を用います。 このとき、説明変数\( x \)をおもりの重さ、目的変数\( y \)をばねの伸び量とします。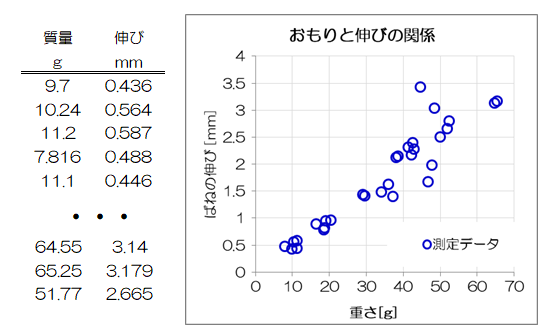
グラフを見ると、ばねにつるしたおもりの重さとばねの伸び量には比例関係があるように見て取れます。
そこで、回帰モデルとして次の比例関係 = 線形回帰モデルを想定します（おもりなしなら伸び量0のため）。
\[
y=kx
\tag{2.1.1-1}
\]
このときの𝑘（ばね定数）を求めるのが今回の目的になります。なお、𝑘を回帰係数と呼びます。
各データの組にID付けを行い、\( (x_i,y_i) \ (i=1,2,\cdots,n) \)で表します。 もし、測定誤差がなければ、（2.1.1-1）式に\( x_i \)を代入した値と測定値\(y_i\)は一致するはずです。 しかしながら、実際は測定誤差によってこれらにはズレが生じます。 このズレを残差と呼び\( \epsilon_i \)で表します。
\[
\epsilon_i = y_i - kx_i
\tag{2.1.1-2}
\]
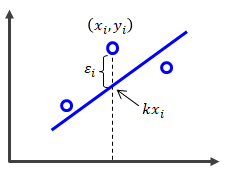
また目的変数、説明変数、残差をn次元ベクトルとして表すことで（2.1.1-2）式は次のように表現できます。
\[
\begin{pmatrix}
\epsilon_1
\\
\epsilon_2
\\
\vdots
\\
\epsilon_n
\end{pmatrix}
=
\begin{pmatrix}
y_1 - kx_1
\\
y_2 - kx_2
\\
\vdots
\\
y_n - kx_n
\end{pmatrix}
\
\leftrightarrow
\
\boldsymbol{\epsilon}
=
\boldsymbol{y}-Xk
\tag{2.1.1-3}
\]
ただし、 \( \boldsymbol{\epsilon} = \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{pmatrix} , \quad \boldsymbol{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} , \quad \boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \)
さて、n個分のデータすべてに残差\( \epsilon_i \)が含まれていますが、最小二乗法の前提により、これらの平均は0となるため、単純に\( \epsilon_i \)の和が最も小さくなるモデル、というのは設定できません（∵\( \epsilon_i \)は正負の符号が含まれるため）。そこで、残差ベクトルの大きさ\( \| \epsilon \|^2 \)を最小とする回帰係数𝑘を決めれば、誤差の最も少ないモデルとして扱うことができます。
\[
\begin{eqnarray}
\| \epsilon \|^2
& = &
(\boldsymbol{y} - X k )^t (\boldsymbol{y}-Xk)
\\
& = &
\boldsymbol{y} \boldsymbol{y}^t - \boldsymbol{y}^tXk - kX^t\boldsymbol{y} + kX^tXk
\\
& = &
\boldsymbol{y} \boldsymbol{y}^t - 2 kX^t\boldsymbol{y} + kX^tXk
\end{eqnarray}
\tag{2.1.1-4}
\]
なお、\( (\boldsymbol{y} - X k )^t \)は\( (\boldsymbol{y} - X k ) \)の転置をとったもので1×n行列です。
また、2行目から3行目の移行は\( \boldsymbol{y}^tXk = kX^t\boldsymbol{y} \)を使っています。
今求めたいのは\( \| \epsilon \|^2 \)を最小にする𝑘なので、（2.1.1-4）式は\( k \)を変数とする方程式と捉えます。 このとき\( \| \epsilon \|^2 \)を最小とする𝑘の条件は、（2.1.1-4）式を両辺\( k \)で微分したものが0になること、つまり変曲点をとることです。
\[
\frac{\partial \| \epsilon \|^2 }{\partial k}
=
- 2 X^t\boldsymbol{y} + X^tXk
=
0
\tag{2.1.1-5}
\]
このとき\( X^tX \)はスカラーとなるので、0でなければ\( k \)は求まります。
\[
k=(X^tX)^{-1}X^t\boldsymbol{y}
\tag{2.1.1-6}
\]
\( k \)が決まったことで、回帰モデルの（2.1.1-1）式が決まります。
今回の例でいえば、下図の“\( y=0.0512x \)”が（2.1.1-1）式に該当します。
先ほどの例ではy切片 = 0のモデルを扱いましたが、y切片が0でない場合は次のようにして線形回帰係数を算出します。
定数項を含む回帰係数を\( c_0,c_1 \)とします。
\[
y=c_1x+c_0
\tag{2.1.1-7}
\]
n個のデータ組に対し、（2.1.1-3）式同様に行列表現すると次のようになります。
\[
\begin{pmatrix}
\epsilon_1
\\
\epsilon_2
\\
\vdots
\\
\epsilon_n
\end{pmatrix}
=
\begin{pmatrix}
y_1 - c_1x_1-c_0
\\
y_2 - c_1x_2-c_0
\\
\vdots
\\
y_n - c_1x_n-c_0
\end{pmatrix}
\
\leftrightarrow
\
\boldsymbol{\epsilon}
=
\boldsymbol{y}-Xk
\tag{2.1.1-8}
\]
ただし、 \( \boldsymbol{\epsilon} = \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{pmatrix} , \quad \boldsymbol{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} , \quad \boldsymbol{x} = \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{pmatrix} , \quad \boldsymbol{c} = \begin{pmatrix} c_0 \\ c_1 \end{pmatrix} \)
\( \boldsymbol{c} \)は回帰係数ベクトルになります。計算することは同じで、残差ベクトルの大きさを最小にするベクトル\( \boldsymbol{c} \)を求めます。
\[
\begin{eqnarray}
\| \epsilon \|^2
& = &
(\boldsymbol{y} - X \boldsymbol{c} )^t (\boldsymbol{y}-X \boldsymbol{c})
\\
& = &
\boldsymbol{y} \boldsymbol{y}^t - \boldsymbol{y}^tX\boldsymbol{c} - (\boldsymbol{c}X)^t\boldsymbol{y} + (\boldsymbol{c}X)^tX\boldsymbol{c}
\\
& = &
\boldsymbol{y} \boldsymbol{y}^t - 2 (\boldsymbol{c}X)^t\boldsymbol{y} + (\boldsymbol{c}X)^tX\boldsymbol{c}
\end{eqnarray}
\tag{2.1.1-9}
\]
2行目から3行目の移行は\( \boldsymbol{y}^tX\boldsymbol{c} = (\boldsymbol{c}X)^t\boldsymbol{y} \)を使っています。
ここでy切片 = 0のときと異なるのは、\( \| \epsilon \|^2 \)をベクトルで微分するところにあります。 とはいえ特段難しい話ではなく、
\[
\begin{eqnarray}
& \frac{\partial \boldsymbol{c}}{\partial \boldsymbol{c}} &
=
\begin{pmatrix}
\frac{\partial c_0}{\partial \boldsymbol{c}}
\\
\frac{\partial c_1}{\partial \boldsymbol{c}}
\end{pmatrix}
=
\begin{pmatrix}
\frac{\partial c_0}{\partial c_0} & \frac{\partial c_0}{\partial c_1}
\\
\frac{\partial c_1}{\partial c_0} & \frac{\partial c_1}{\partial c_1}
\end{pmatrix}
=
\begin{pmatrix}
1 & 0
\\
0 & 1
\end{pmatrix}
\\
& \frac{\partial \boldsymbol{c}^t}{\partial \boldsymbol{c}} &
=
\begin{pmatrix}
\frac{\partial c_0}{\partial \boldsymbol{c}} & \frac{\partial c_1}{\partial \boldsymbol{c}}
\end{pmatrix}
=
\begin{pmatrix}
\frac{\partial c_0}{\partial c_0} & \frac{\partial c_1}{\partial c_0}
\\
\frac{\partial c_0}{\partial c_1} & \frac{\partial c_1}{\partial c_1}
\end{pmatrix}
=
\begin{pmatrix}
1 & 0
\\
0 & 1
\end{pmatrix}
\end{eqnarray}
\]
を用いることで計算できます。
\[
\frac{\partial \| \epsilon \|^2 }{\partial \boldsymbol{c}}
=
- 2 X^t\boldsymbol{y} + X^tX\boldsymbol{c}
=
0
\tag{2.1.1-10}
\]
この式から\( X^tX \)が逆行列を持てば、回帰係数ベクトル\( \boldsymbol{c} \)は求まります。
\[
\boldsymbol{c}
=
(X^tX)^{-1}X^t\boldsymbol{y}
\tag{2.1.1-11}
\]
