2．1．2．二変数の多項式回帰
前節では二変数の線形回帰を扱いました。 その考え方を発展させて、今度は多項式の回帰モデルを扱います。といっても難しくはありません。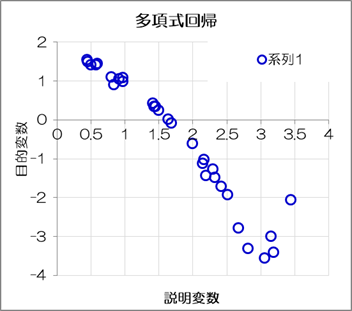
n個のデータで構成される上記グラフを三次多項式の回帰モデルで関数化します。
\[
y
=
c_3 x^3 + c_2 x^2 + c_1 x + c_0
\tag{2.1.2-1}
\]
線形回帰のときと同様、残差\(\boldsymbol{\epsilon}\)、目的変数\(\boldsymbol{y}\)、回帰係数\(\boldsymbol{c}\)をベクトルとし、説明変数をn×4行列Xで表します。
\[
\boldsymbol{\epsilon}
=
\begin{pmatrix}
\epsilon_1
\\
\epsilon_2
\\
\vdots
\\
\epsilon_n
\end{pmatrix}
, \quad
\boldsymbol{y}
=
\begin{pmatrix}
y_1
\\
y_2
\\
\vdots
\\
y_n
\end{pmatrix}
, \quad
\boldsymbol{x}
=
\begin{pmatrix}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{pmatrix}
\]
\[
X
=
\begin{pmatrix}
1 & x_1 & x_1^2 & x_1^3
\\
1 & x_2 & x_2^2 & x_2^3
\\
\vdots & \vdots & \vdots & \vdots
\\
1 & x_n & x_n^2 & x_n^3
\end{pmatrix}
\]
後は線形回帰と全く同様に、残差ベクトルの大きさを最小にするよう回帰係数ベクトル\(\boldsymbol{c}\)を求めるだけです。
一応式は記述しておきますが、全く同じであることを確認してください。
\[
\boldsymbol{\epsilon}
=
\boldsymbol{y}-Xk
\tag{2.1.2-2}
\]
\[
\| \boldsymbol{\epsilon} \|^2
=
\boldsymbol{y} \boldsymbol{y}^t - 2 (\boldsymbol{c}X)^t\boldsymbol{y} + (\boldsymbol{c}X)^tX\boldsymbol{c}
\tag{2.1.2-3}
\]
\[
\frac{\partial \| \epsilon \|^2 }{\partial \boldsymbol{c}}
=
- 2 X^t\boldsymbol{y} + X^tX\boldsymbol{c}
=
0
\tag{2.1.2-4}
\]
\[\boldsymbol{c}
=
(X^tX)^{-1}X^t\boldsymbol{y}
\tag{2.1.2-5}
\]
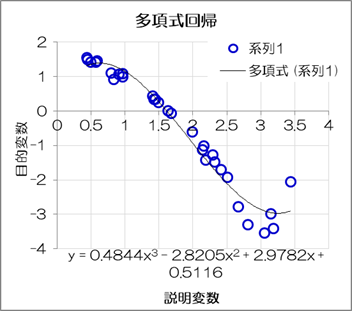
以上の式から算出される回帰係数は下図の通りです。
2．1．3．二変数の非線形回帰
回帰モデルは、線形や多項式だけでなく、指数関数、三角関数、反比例関数、双曲関数やそれらの複合関数など、多岐にわたって適用可能です。 しかも簡単に回帰モデルを作ることができます。ここでは指数関数を例にとって説明します。
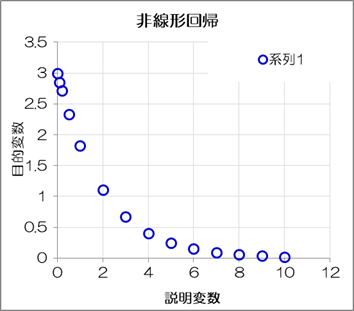指数関数を次のようにとります。
\[
y=c_o \exp ( c_1 x )
\tag{2.1.3-1}
\]
このままだと次式の形にすることはできません（（2.1.1-8）、（2.1.2-2）式と同じ）。
\[
\boldsymbol{\epsilon}
=
\boldsymbol{y}-Xk
\tag{2.1.3-2}
\]
そこで（2.1.3-1）式の両辺のlogをとると、線形式で表現できます。
\[
\log y
=
\log \{ c_o \exp ( c_1 x ) \}
=
c_1x + \log c_0
\tag{2.1.3-3}
\]
こうすることで、指数関数の回帰モデルは（2.1.3-2）式に変形できます。
このとき、説明変数ベクトル、回帰係数ベクトル、目的変数行列は次のようになります。
\[
\boldsymbol{Y}
=
\begin{pmatrix}
\log y_1
\\
\log y_2
\\
\vdots
\\
\log y_n
\end{pmatrix}
, \quad
\boldsymbol{c}
=
\begin{pmatrix}
c_0'
\\
c_1
\end{pmatrix}
, \quad
X
=
\begin{pmatrix}
1 & x_1
\\
1 & x_2
\\
\vdots & \vdots
\\
1 & x_n
\end{pmatrix}
\]
ただし、\( c_0' = \log c_0 \)
つまり、この指数関数の回帰モデルを算出する場合は説明変数𝒚のlogをとって、あとは線形回帰の計算（2.1.2-2）～（2.1.2-5）式を適用すればよいことになります。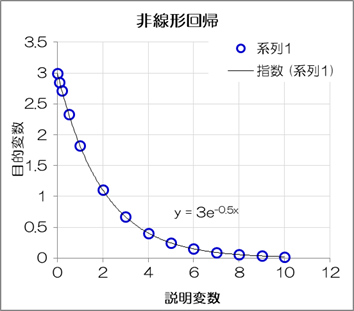
2．2．多変数の最小二乗法
2.1節では説明変数が1つの場合を見てきました。
しかし、実際の現象は1つの変数で説明できるようなものは稀で、複数の変数 = 影響が複雑に絡み合っています。 例えば容器内のガスの温度Tは、容器内の圧力P、体積V、物質量（モル数）Nで決まります。 この場合、目的変数はT、説明変数はP、V、Nの三つになります（気体の状態方程式をイメージしてください）。
このような複数の変数を考慮した回帰モデルを作るのが本節の目的になります。
とはいえ、多変数の回帰係数の算出は、一変数（多項式）の回帰係数算出方法を少し応用するだけです。
次のように、説明変数が三種類あるデータの組がn個あるとします。
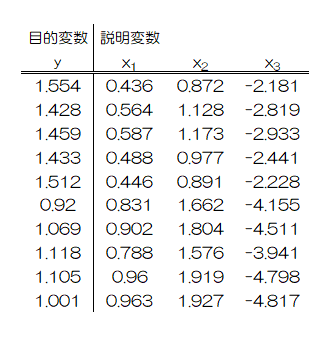このとき、次のような回帰モデルを考えます。
\[
y
=
c_3 x_3 + c_2 x_2 + c_1 x_1 + c_0
\tag{2.2-1}
\]
この式は、二変数の多項式回帰で出てきた（2.1.2-1）式の変数を\(x_3=x^3,cx_2=x^2,x_1=x \)と置き換えたものと等しいことがわかります。
\[
y
=
c_3 x^3 + c_2 x^2 + c_1 x + c_0
\tag{2.1.2-1}
\]
つまり、説明変数行列𝑋を次のように書き換えるだけです。
\[
X
=
\begin{pmatrix}
1 & x_{11} & x_{12} & x_{13}
\\
1 & x_{21}& x_{22} & x_{23}
\\
\vdots & \vdots & \vdots & \vdots
\\
1 & x_{n1} & x_{n2} & x_{n3}
\end{pmatrix}
\]
他は2.1.2節と同じです。
\[
\boldsymbol{\epsilon}
=
\begin{pmatrix}
\epsilon_1
\\
\epsilon_2
\\
\vdots
\\
\epsilon_n
\end{pmatrix}
, \quad
\boldsymbol{y}
=
\begin{pmatrix}
y_1
\\
y_2
\\
\vdots
\\
y_n
\end{pmatrix}
, \quad
, \quad
\boldsymbol{c}
=
\begin{pmatrix}
c_0
\\
c_1
\\
c_2
\\c_3
\end{pmatrix}
\]
結果、以降の計算式も（2.1.2-2）～（2.1.2-5）式をそのまま利用して回帰係数ベクトルを算出できます。
