ニューラルネットワーク
4．ニューラルネットワークの学習
4．1．ニューラルネットワークの学習
2.3節で単純パーセプトロンの学習について説明しました。 この学習では線形分離できない問題には対応できませんでした。 そこでニューラルネットワークは、3.2節でみた活性化関数をニューロンに適用することで、この問題に対応しました。ニューラルネットワークの学習もこれまで同様、データから“重み”を自動で決定します。 さらにこの“重み”を使って、別のデータの入力に対し、予測や判別を行うのが目的です。
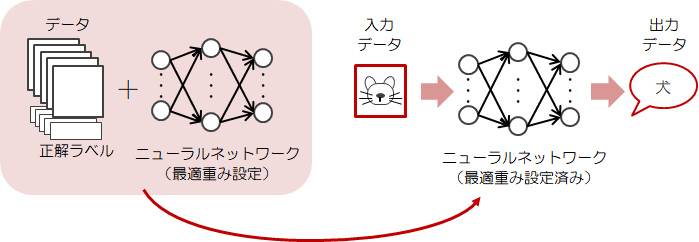そのため“重み”の設定が終わったら、今度はその「“重み”に汎用性があるか？」を確認しなければなりません。
というのも、学習に使ったデータだけを判別できても意味がないからです。そのためには先ほどのデータを、1つは特徴抽出用の訓練データ（教師データ）、もう1つは確認用のテストデータとして分割し、訓練データで得た“重み”を使ってテストデータで確認をする、という手順をとります。
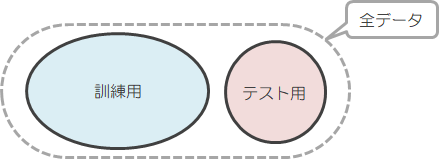ただ残念ながら、得られた“重み”が訓練データには適合するけどテストデータには適合しない、といった場合があります。
この特定のデータに対してのみ適合するような状態を過学習といいます。
“重み”の設定は、この過学習をさけつつ、正解率の高いものを見つけなければなりません。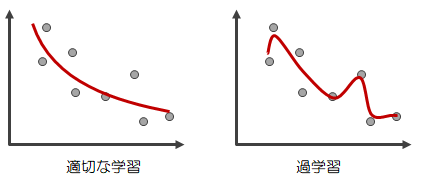
4．2．損失関数
ニューラルネットワークの学習がどれだけうまくいっているか？を測る指標が損失関数です。 損失関数によって「教師データに対してどれだけズレをもっているか？」を知ることで、現状のニューラルネットワークの性能を定量的に評価できます。 つまり、損失関数の値を小さくできれば、教師データに対するズレも小さくなる、ということです。ニューラルネットワークの学習は、この損失関数の値を可能な限り小さくする“重み”を見つけ出すことです。
損失関数として用いられる関数はいくつもありますが、ここでは次の2つについて説明していきます。
- 二乗和誤差
- 交差エントロピー誤差
4．2．1．二乗和誤差
\( z_k \)をニューラルネットワークの出力値、\( t_k \)を教師データとします。このとき、二乗和誤差は次のようにして求めます。
\[
E
=
\frac{1}{2} \sum_{k=1}^n (z_k - t_k )^2
\tag{4.2.1-1}
\]
出力値\( z_k \)と、それに対応する教師データ\( t_k \)の差（差分）\( z_k - t_k \)をとれば、正解とのずれがわかります。
しかしながら、差分は正負両方の値をとれるので、差分をそのまますべて足し合わせると“0”になることもあり得ます。
ズレはあるのにその総和は“0”では、何を評価しているのかわかりません。
その問題を解消するために差分を二乗することで正負の符号はなくなり、正のみの値をとることができます
（絶対値でも同じことが言えますが、二乗する方が計算上のメリットは大きいためです）。差分の二乗はある種、教師データからのズレを距離で測る、と考えることができます。
二乗和誤差はズレの距離の総和であり、ズレの距離が小さければ小さいほど、出力値は正しい結果を出力している、と考えることができます。
学習では損失関数の出力値による微分を使うので、その結果を示します。\[
\frac{\partial L}{\partial z_k}
=
(z_k - t_k)
\tag{4.2.1-2}
\]
4．2．2．交差エントロピー誤差
\( z_k \)をニューラルネットワークの出力値、\( t_k \)を教師データとします。このとき、交差エントロピー誤差は次のようにして求めます。
\[
E
=
- \sum_{k=1}^n t_k \log z_k
\tag{4.2.2-1}
\]
学習では損失関数の出力値による微分を使うので、その結果を示します。\[
\frac{\partial L}{\partial z_k}
=
-\frac{\partial t_k}{\partial z_k}
\tag{4.2.2-2}
\]
4．2．3．損失関数の役割
さて、損失関数として使用する二乗和誤差（4.2.1-1）式、交差エントロピー誤差（4.2.2-1）式は、“重み”を見た目には含んでいませんが、出力の算出過程で含んでいます。 ということは、“重み”を変化させれば損失関数の値も変化することになります。 この性質によって、ニューラルネットワークの学習という機能が成立します。確認のために3.3節のまとめた式に登場してもらいます。
| 入力層→隠れ層1 | ： | \( Y^1 = g^1(XW^1) \) |
| 隠れ層1→隠れ層2 | ： | \( Y^2 = g^2(Y^1W^2) \) |
| ・・・ | ||
| 隠れ層n-1→隠れ層n | ： | \( Y^n = g^n(Y^{n-1}W^n) \) |
| 隠れ層n→出力層 | ： | \( Z = h(Y^nW^{n+1}) \) |
こういうと口で言うのは簡単ですが、実は現段階で重みは何も決まっていない状態です。 それで計算しろ、といわれてもどうすればいいのか検討もつきません。それに重み\( W^l \)を動かす、といってもどう動かせばいいのか、さっぱりわかりません。
次節では、この点について話を進めていきます。
4．3．勾配法
「重み\( W \)を調整して損失関数\( L \)を小さくする」にはどうすればよいでしょう？そのためには、重み\( W \)を変えたときに損失関数\( L \)がどれだけ変わるか、つまり\( L \)に対する\( W \)の感度を知ることが重要になります。 この変数に対する関数の感度を知る方法に偏微分があります。
例えば、多変数関数\( y=f(x_1, x_2 )=2x_1+4x_2 \)の偏微分を計算すると
\[
\frac{\partial y}{\partial x_1}
=
2
, \quad
\frac{\partial y}{\partial x_2}
=
4
\]
になります。
これは\( x_1 \)と\( x_2 \)を同じだけ動かすと\( x_2 \)の方が2倍𝑦を大きく変化させられます。
つまり\( x_2 \)の方が感度が高い、ということです。
また、ベクトル\( \bf{x}=(x_1, x_2 ) \)として\( y \)を偏微分すればそれもまたベクトルとして扱え、勾配といいます。\[
\frac{\partial y}{\partial \bf{x} }
=
\left( \frac{\partial y}{\partial x_1}, \quad \frac{\partial y}{\partial x_2} \right)
\tag{4.3-1}
\]
行列による微分も勾配として扱い、行列と同じサイズになります。
\[
\frac{\partial y}{\partial X }
=
\begin{pmatrix}
\displaystyle \frac{\partial y}{\partial x_{11}} & \cdots & \displaystyle \frac{\partial y}{\partial x_{1n}}
\\
\vdots & \ddots & \vdots
\\
\displaystyle \frac{\partial y}{\partial x_{m1}} & \cdots & \displaystyle \frac{\partial y}{\partial x_{mn}}
\end{pmatrix}
\tag{4.3-2}
\]
\( ( W \in R^{n \times m} , \quad \frac{\partial L}{\partial W} \in R^{n \times m} ) \)
勾配は「ある地点における関数の値を最も減らす方向」を示します。 この特徴は、今問題としている「重み\( W \)を調整して損失関数\( L \)を小さくする」に使えそうです。 そこで登場するのが勾配法です。
勾配法は、ある地点で最も勾配のきつい方向にある距離進み、進んだ地点で最も勾配のきつい方向にある距離進み、・・・を繰り返して、最終的に勾配の無くなる点=最小と思われる点に到達する、という方法です。
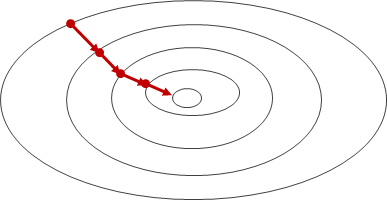“思われる”としたのは、勾配法は必ずしも最小値に行きつく保証はなく、極小値（局所的な最小値）にたどり着くことが多々あるからです。
とはいえ、どこに向かえばよいか全くわからない状態では、勾配のこの性質に頼るのは自然でしょう。そこで、この勾配法にもとづく最適な重み\( W \)の探索手順を、数式を使って表してみます。
まずは損失関数\( L \)の重み\( W \)による勾配\( \partial L / \partial W \)を求めます。
次に、その勾配の方向に向かってある量移動します。 このときの“ある量”は、\( W \)の勾配に係数\( \eta \)を掛けたものとします。 調整後の重みを\( \tilde{W} \)とすると、
\[
\tilde{W}
=
W - \eta \frac{\partial L}{\partial W}
\tag{4.3-3a}
\]
成分表示すれば\[
\tilde{w_{ij}}
=
w_{ij} - \eta \frac{\partial L}{\partial w_{ij}}
\tag{4.3-3b}
\]
となります。
調整に引き算を使っているのは、前述の例\( y=f(x_1, x_2 )=2x_1+4x_2 \)を使えば、その勾配が(\( 2x_1, 4x_2 \))と最小点から遠ざかる向きで出てくるので、反転させる必要があるためです。
このときの移動量を決める係数\( \eta \)を学習率といいます。
学習率はセッティング要素のため、人が決めることになります。新たに調整された重み\( \tilde{W} \)を用いて損失関数を再計算します。 この損失関数の\( \tilde{W} \)による勾配を求めます・・・（以降繰り返し）。
これを続けていけば、重み\( W \)の勾配は小さくなっていき、勾配が0、つまり損失関数\( L \)が（局所的に）最小となる点に限りなく近づけることで、学習を終えます。
