連続体力学
1.連続体
1.1.連続体力学の位置づけ
力学では物体を「一つの質量を持った点=質点」、あるいは「変形しない物体=剛体」とみて現象を捉えていました。 しかしながら、実際の物体は変形します。 そこで、物体の変形を力学によって表現しようと試みたのが連続体力学です。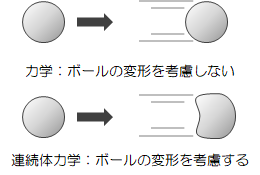
図1.1-1 力学と連続体力学
さて、物体は大きく分けて、固体、液体、気体の三種類の状態に分類され、特に“液体”と“気体”を合わせて流体と呼びます。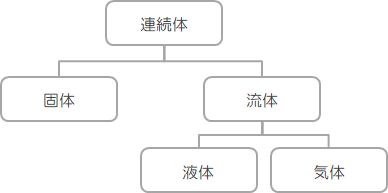
図1.1-2 連続体の分類
“固体”と“液体”の大きな特徴差は「変形のしやすさ」です。例えば立方体状の固体、液体、気体があるとします。 固体は放置してもほとんど変形しませんが、液体は形状を維持できず流れを伴ってびちゃ~っと床に広がります。 気体に至っては、見えはしませんが例えば匂いが一気に広まることから考えても液体以上に形を変えます(拡散します)。
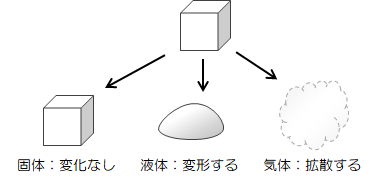
図1.1-3 流体と固体の違い
このような変形の違いは、重力場の中の静止状態で固体にはせん断力が働く ⇔ 流体にはせん断力が働かない
ことによるものです。 つまり、固体内部の各点は重力を受けてもそれに打ち勝つ力が働いているのに対し、流体内部の各点はその重力に打ち勝つようなズレ方向の力が働かない、ということです。そのため、変形(力学的にいえば運動)の記述は固体と流体で異なります。 従って本サイトでは、固体と流体に共通する内容を連続体力学(本ページ)で述べ、個別の内容については弾性理論と流体力学ページで述べることにします。
1.2.連続体仮定
物体を細かく分割していくと、やがて分子や原子といった離散的(不連続)な物質にまで分けられます。 しかしながら我々が現実に扱う物理現象は、多数の分子の平均的な運動を捉えられれば十分で、個々の分子の運動まで細かく見る必要はありません。 つまり、「物体は、空間内にすきまなく物質を詰め込んだもの」
として近似的に取り扱っても、現象を十分把握できます。 このような仮定を連続体仮定と呼びます。 また、連続体とは上記仮定に基づいた物体のことです。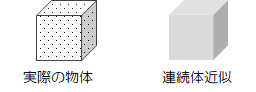
図1.2-1 連続体近似
この定義からわかるように、連続体仮定には有効になるための条件があります。 それは、分子間相互作用など微視的な影響を十分無視できる、さらに言えば分子間距離に比べて連続体が十分大きいことです。1.3.連続体力学で用いる数学
1.3.1.テンソル表記
連続体力学は物体の変形を扱う学問です。 従って、物体内部の位置は“(三次元)ベクトル”で表します。 さらに、物体の変形に伴う位置変化は、多重線型変換を用いて表現されます (具体的には(2.2.2-4)式を参照ください)。 この多重線型変換は、(三次元)ベクトルを変数とする多重線型関数であり、“テンソル”と呼びます。(2.2.2-4)式は、行列部分(3×3行列)が多重線型変換であり、それをTで表せば非常に簡単な計算式 \[ \boldsymbol{r'} - \boldsymbol{r} = T d \boldsymbol{r} \] で表せます。
(2.2.2-4)式の例で言えば、ベクトルは3成分、テンソルは9成分とたくさんあるため、テンソル演算の表記を成分で律義に表現しようとすると、は非常に煩雑になります。 そこで、アインシュタインの規約(またはアインシュタインの縮約記法)というルールに基づき、簡略化した表現方法を用います。 この表現方法に慣れておかないと、連続体力学で現れる式が一体何を意味しているのか?がさっぱりわからなくなってしまいます。
●アインシュタインの規約
ベクトルやテンソル成分の添字(例えばi,j,kなど)について、演算で総和をとるような場合、1つの項に2度繰り返して現れる添字についてはその添字についての和をとります。
具体的には次のようになります。
そこで、本節では連続体力学で多用される数学についての参考書を紹介しておきます。
それについては、次のように考えることができます。
私たちが扱う連続体の大きさは小さくてもせいぜい数um(10-6m)程度であるのに対し、標準状態の大気における分子間距離は数nm(10-9m)程度と非常に小さいものです。 計算上無視できるオーターとしては、対象としている桁数より二桁程度です (例えば100に対し1以下なら無視。ただし、時と場合によりますが)。 従って、連続体の微分を扱ってもせいぜい10-8m程度ですので分子間距離に対して十分大きいと考えられ、連続体の微分方程式はそのまま連続体として扱っても問題ない、と考えられます。
具体的には次のようになります。
\[
\boldsymbol{r}
=
r_i \boldsymbol{e_i}
\quad ( =
r_x \boldsymbol{e_x} + r_y \boldsymbol{e_y} + r_z \boldsymbol{e_z}
=
\sum_{i=x,y,z} r_i \boldsymbol{e_i}
)
\]
(一つの項にiが2回出てくる)
\[
\frac {\partial u_i}{\partial \boldsymbol{r}} d\boldsymbol{r}
=
\frac {\partial u_i}{\partial r_j} dr_j
\quad ( =
\frac {\partial u_i}{\partial x} dx +
\frac {\partial u_i}{\partial y} dy +
\frac {\partial u_i}{\partial z} dz
=
\sum_{j=x,y,z} \frac {\partial u_i}{\partial r_j} dr_j
)
\]
(一つの項にjが2回出てくる)
\[
u_{xx} + u_{yy} + u_{zz}
=
u_{ii}
\]
対角項1つだけを表現したい場合は、クロネッカーのデルタを使って次のように表現します。
(一つの項にiが2回出てくる)
\[
u_{xx}
=
\delta_{ij} u_{ii} \quad (i=x)
\]
1.3.2.連続体力学に必要な数学の参考書
連続体力学は、数学の力を使うことで非常に理解の幅が広がり、深さが増します。 特に、数学的に証明されているものは厳密性を持っているので、無条件に取り込み式変形することで、現象把握をよりスムースに行えるようになります。 ただ、残念なことに連続体力学における数学的表現は、力学と比べるとはるかに難解で読みにくいものになります。そこで、本節では連続体力学で多用される数学についての参考書を紹介しておきます。
(1)微分積分
連続体力学では、多変数に関する一次近似を多用することから、テイラー展開、偏微分について理解を深めておくことをおすすめします。(2)ベクトル解析・テンソル解析
連続体力学の表現や証明はこの範囲にかなり依存しています。 テンソルによって式の表記は非常に簡素化されます。 また、勾配(grad)、発散(div)、回転(rot)といったベクトルの微分や、体積分⇔面積分⇔線積分の変換(グリーン、ガウスの定理)を用いることで、連続体の現象説明は非常に楽に進みます。(3)線形代数
(2)の基礎となる部分ですので抑えておくと理解が進みます。 特に連続体力学では、座標系の選択に絡む基底の考え方や内積が重要となります。1.4.連続体の微分
連続体の諸問題を扱う際、数多くの微分方程式に遭遇します。 これらの式は無限小の概念を扱うため、連続体仮定がそのまま適用できないのではないか?という疑問がわいてきます。それについては、次のように考えることができます。
私たちが扱う連続体の大きさは小さくてもせいぜい数um(10-6m)程度であるのに対し、標準状態の大気における分子間距離は数nm(10-9m)程度と非常に小さいものです。 計算上無視できるオーターとしては、対象としている桁数より二桁程度です (例えば100に対し1以下なら無視。ただし、時と場合によりますが)。 従って、連続体の微分を扱ってもせいぜい10-8m程度ですので分子間距離に対して十分大きいと考えられ、連続体の微分方程式はそのまま連続体として扱っても問題ない、と考えられます。


