連続体力学

3．連続体に働く力

3．1．面積力と体積力

物体に働く力を大別すると次の二つに分類されます。

（1）体積力

物体の体積や質量に比例する力で、重力や電磁気力などの非接触力が該当します。物体を微小体積要素（体積素片）に分割し、単位体積あたりの体積力\( f_b \ \)をとしたとき、体積素片と物体全体に働く体積力は次式で表せます。

\[ d \bf{ F_b } = \bf { f_b } dV \quad \bf{ F_b } = \int \bf { f_b } dV \]

（2）面積力

連続体を微小要素分割したとき、要素間の境界面（面積素片）を通して働く面積に比例する力で、圧力などの接触力が該当します。また、分子の自由混合（境界面を分子が自由に行き交う状態）によっても面積力が発生します。自由混合による面積力は、境界面を境に質量の交換が行われていることと同じであり、運動量変化が生じる→力積が発生することによって説明可能です（基本的には流体での現象です）。さて、面積素片は大きさ\( dS \)を持つとともに表面の外法線に沿う向きも持つのでベクトル\( d \bf{ S } \)で定義します。単位面積あたりに作用する面積力\( f_s \)をとしたとき、面積素片と物体全体に働く面積力は次式で表せます。

\[ d \bf{ F_s } = \bf { f_s } d \bf{ S } \quad \bf{ F_s } = \oint \bf { f_s } \bf{ S } \]

図3.1－1　面積素片ベクトル

3．2．応力

物体は原子や分子によって構成されています。
変形を受けない物体は安定状態にあり、その分子配列は力学的にも熱的にも平衡状態にあります。それに対し物体が変形すれば、それに伴い分子配列にも変化が生じます。分子間には相互作用力が働いており、それは分子間距離に依存します（クーロン力の引力、斥力がイメージしやすいと思います）。従って、分子配列が変化することで力学的均衡は崩れ、物体内部の平衡状態は保てなくなります。ところが、分子間の相互作用力は分子配列の変化を抑える方向で発生します（距離が離れれば引力が、近づけば斥力が働くことによります）。これは復元力であり変形が生じて初めて働くもので、内部応力と呼びます。

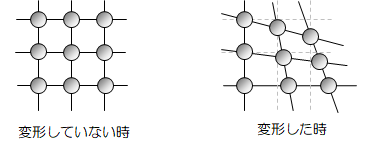
図3.2－1　ミクロ視点での物体の変形

内部応力には次のような性質があります。
分子間の相互作用力の影響はせいぜい分子間の距離程度であり、巨視的に見る連続体力学ではその作用半径は近似的に0とみなすことができます。従って、物体に遠隔力が作用しない場合、物体内部の各要素に働く力は面積力の合力とみてよいことになります。そのため応力は、物体内部に定義した微小面積に働く単位面積あたりの力を指し、圧力と同じ単位[N/m²] = [Pa]になります。

3．3．応力テンソル

ここでは応力を数式化していきます。
物体を体積素片\( dV \)で分割すれば、各体積素片と物体全体に働く力は単位体積当たりの力ベクトルを\( \bf{ f } \)を用いて次式で表せます。

\[ d \bf{ F } = \bf { f } dV \quad \bf{ F } = \int \bf { f } dV = \left( \int f_i dV \right) \tag{3.3-1} \]

\( \bf{ F } \)はベクトルなのでx、y、z方向の3成分を持ち、それぞれが直交しているため各成分は独立に決まります。そこでx成分のみに着目して話を進めれば、残りy、zについても同様に成り立ちます。
（3.3－1）式の体積分は、数学の定理（ベクトル解析：ガウスの定理）によって面積分に変換できます。このとき新しいベクトル\( \sigma_x \)を導入して

\[ \begin{eqnarray} \int f_x dV &= \int \nabla \bf{\sigma_x} dV \\ &= \oint \bf{\sigma_x} \cdot d \bf{S} \\ &= \oint \sigma_{ik} dS_i \\ \end{eqnarray} \tag{3.3-2} \]

とできます。（3.3－2）式の右式から\( \sigma_x \)は[N/m2]の単位を持つベクトルであり、応力の意味を持ちます。この\( \sigma_x \)をx軸方向の応力ベクトルと呼びます。なお、応力ベクトル\( \sigma_x \)は必ずしも面に垂直な方向のみ作用するわけではありません。そこで、面に垂直な方向（面外方向）の応力を法線応力、面内方向の応力を接線応力と呼んで区別します。

さて、上述の内容はy、z軸方向についても成り立つので（3.3－2）式を一般化します。

\[ \int f_o dV = \oint \sigma_{ij} dS_j \tag{3.3-3} \]

\( \sigma_{ij} \)は9個の成分を持ち二階のテンソルになることから、応力テンソルと呼びます。

\[ \sigma = ( \sigma_{ij} ) = \begin{eqnarray}\left( \begin{array}{ccc} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{array} \right)\end{eqnarray} \tag{3.3-4} \]

（おそらくこの説明は数学に頼りすぎていて現象的にわかりにくいと思いますので、別途補足説明したいと思います。）

次に、応力テンソルが対称テンソルであることを示します。
物体内のある体積要素に働く力のモーメントに着目し、物体の体積素片\( dV \)に作用する力のモーメントを計算します。

\[ ( F_i dV ) x_j - (F_j dV) x_i = ( F_i x_j - F_j x_i ) dV \tag{3.3-5} \]

物体全体に作用する力のモーメントはこれを全体積にわたって積分すればよく、

\[ M_{ij} = \int ( F_i x_j -F_j x_i ) dV \tag{3.3-6} \]

となります。\( F_i \)と応力テンソル\( \sigma_{ik} \ \)の間には

\[ F_i = \nabla \bf{\sigma_i} = \frac{\partial \sigma_{ij}}{\partial x_j} \tag{3.3-7} \]

が成り立つので（（3.3－2）式参照）、（3.3－6）式は部分積分と各座標軸の直交性を考慮して次のように書き換えられます。

\[ \begin{align} M_{ij} &= \int \left( \frac{ \partial \sigma_{ik} }{ \partial x_k } x_j - \frac{\partial \sigma_{jk}}{\partial x_k} x_i ) \right) dV \\ &= \int \frac{ \partial }{ \partial x_k} ( \sigma_{ik} - \sigma_{jk} ) dV - \int \left( \sigma_{ik} \frac{ \partial x_j }{ \partial x_k} - \sigma_{jk} \frac{ \partial x_i }{ \partial x_k} \right) dV \\ &= \int \frac{ \partial }{ \partial x_k} ( \sigma_{ik} - \sigma_{jk} ) dV - \int \left( \sigma_{ik} \ \delta{jk} - \sigma_{jk} \ \delta_{ik} \right) dV \end{align} \]

\[ \left( \because \begin{eqnarray} \frac{\partial x_i}{\partial x_k} = \delta_{ik} = \begin{cases} 1 \quad (i=k) \\ 0 \quad (i \neq k) \end{cases} \end{eqnarray} \right) \]

右辺第二項の被積分関数内にある\( \sigma_{ik}, \ \delta_{jk} \ \)は、結局\( \sigma_{ik} \delta_{jk} = \sigma_{ij} \ \)の関係を持ちます。この関係とガウスの定理を用いて上式はさらに書き換えられます。

\[ \begin{align} M_{ij} &= \int \frac{ \partial }{ \partial x_k } ( \sigma_{ik} x_j - \sigma_{jk} x_i ) dV - \int ( \sigma_{ij} - \sigma_{ji} ) dV \\ &= \int \frac{ \partial }{ \partial x_k } ( \sigma_{ik} x_j ) dV - \int \frac{ \partial }{ \partial x_k } ( \sigma_{jk} x_i ) dV - \int ( \sigma_{ij} - \sigma_{ji} ) dV \\ &= \oint \sigma_{ik} x_j df_k - \oint \sigma_{jk} x_i df_k - \int ( \sigma_{ij} - \sigma_{ji} ) dV \\ &( \because ガウスの定理により体積分を面積分に変換 ) \\ &= \oint ( \sigma_{ik} x_j - \sigma_{jk} x_i ) df_k \end{align} \tag{3.3-8} \]

物体全体に働く力は物体表面に沿った面積分のみで表せます。従って、力のモーメントもまた物体表面に沿った面積分のみで表せなければなりません。つまり、（3.3－8）式の右辺第二項は恒等的に0でなければならず、

\[ \sigma_{ij} = \sigma_{ji} \]

を満足しなければなりません。これは応力テンソルが対称であることを示しています。

4．変形と応力の関係

物体は力を受けると変形するので、変形と応力の間には何らかの関係が存在することになります。この関係が明らかになれば連続体の挙動を予測できることになり、理論的にも実用的にも非常に有用なものとなります。
しかしながら1章でも見たように連続体として扱える物体は幅が広く、1つの統一的な理論ですべてを語ることは（今のところ）できません。従って現在の連続体に関する理論は、その性質に応じて区分された体系ごとに構築されています。
本サイトでは、連続体全般に共通して言える変形を2章、応力を3章でみてきました。ここから先“変形と応力の関係”は、各連続体の性質ごとに見ていくことにします。