1.流体力学
1.1.流体とは
流体は液体と気体を総称したものです。液体と気体は自由に変形し、その運動は“流れ”として認識される共通な特徴を備えています。 それに対し固体は変形しにくく、それ自身で形を維持できます。 ただ、このような流体と固体の分類定義ではあまりに定性的で明確な境界が見えてきません。 そこで流体を次のように定義します。
流体=静止状態においてせん断応力が発生せず、法線応力は圧力のみである連続体
上述の定義によると、流体は質量が連続的に分布する媒質=連続体として扱われます。実際に流体を非常にミクロで見ると、分子つまり質点の集まりですが、我々が通常扱うスケールでは連続体として近似的に扱って差し支えない、ということです。 ただし、それにも限界があって、分子の局所的な運動の特徴が如実に現れるようなスケールでは流体を連続体として近似できなくなります。 例えば気体の場合、分子の平均自由行程\( l \)が流れの代表スケール\( L \)に比べて小さければよいとされており、次式が一つの目安となります。\[
K = \frac{l}{L} \lt \frac{1}{5}
\]
上式の\( K \)をクヌッセン数とよびます。なお、代表的スケールという言葉は流体力学ではちょくちょく出てきます。 しかしこれがなかなかのくせもので、「一体どこの寸法?」と悩みの種になることが多々あります。 今回の例で言えば、

図1.1-1 代表的スケールの例
が代表的スケールに該当します。ただし、物体を連続体として近似的に扱う場合、連続体近似(連続体力学参照)が成立しなければなりません。
1.2.流体の運動
流体は、自身の変形しやすさのため非常に複雑な運動をします。 例えば円柱周りの一様流について見ると、その円柱の周りの流れの速さによって流れの様子は異なります。 流れの様子が変わる指標としてレイノルズ数\( Re \)と呼ばれる値を用いると、下図のような違いに分類できます。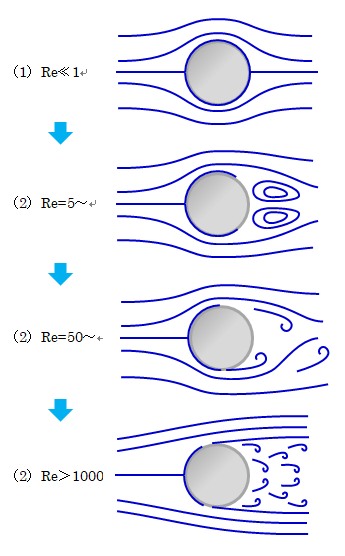
図1.2-1 流れの変遷
Re≪1のとき流体は円柱から離れず、その表面に沿って一様に流れます。 この状態を層流と呼びます。Reが徐々に大きくなるに従い、円柱面の流れに対して後方の面から流れは剥離し、渦ができ始めます。 このような剥離流を伴流と呼びます。
さらにRe=50~500程度になると、今度は剥離した渦が円柱上下で規則正しく発生します。 これをカルマン渦と呼びます。
最後にRe>1000になると円柱後方の渦はランダムに発生し、乱れた流れを形成します。 この乱れを乱流と呼びます。
乱流は渦の発生と密接に関係しており、特にその配置や大きさはランダムなため、決定論的ではなく確率論的な扱いが必要となります。
なお、レイノルズ数\( Re \)は慣性力と粘性力の比で決まり、流体の粘性率\( μ \)、流束\( \boldsymbol{v} \)、流体の密度\( \rho \)、流れの代表スケール\( L \)をとって、
\[
Re = \frac{ \rho v L }{ \mu }
\]
で表します(代表スケールLには円柱面の直径が該当します)。
\( Re \)が小さいと層流、大きいと乱流と判断され、層流から乱流へと遷移するときのレイノルズ数を臨界レイノルズ数と呼びます。
1.3.流体と流れの分類
流体の運動は複雑であり、統一的な理論ですべてを語るは困難です。 そこで流体と流れを分類し、その都度扱いやすい概念(モデル)を用いて考察を行っていくことになります。| 考慮項目 | なし | あり |
|---|---|---|
| 流体の分類 | ||
| 粘性や熱伝導 | 完全流体 | 粘性流体 |
| 粘性の線形性 | 非ニュートン流体 | ニュートン流体 |
| 流体の圧縮性 | 非圧縮性流体 | 圧縮性流体 |
| 流れの分類 | ||
| 時間的変化 | 定常流 | 非定常流 |
| 渦 | ポテンシャル流 | 渦流れ |
| 乱れ | 層流 | 乱流(非定常) |
(1)組み合わせOK
- 完全流体+非圧縮性+定常+ポテンシャル流
- 完全流体+圧縮性+定常
- 完全流体+非圧縮性+非定常+ポテンシャル流
- 粘性流体+非圧縮性+乱流
(2)組み合わせNG
- 完全流体+非圧縮+乱流(乱流は粘性にもとづくため)
- 粘性流体+ポテンシャル流(ポテンシャル流は完全流体が前提)


