3.流体の基礎方程式
3.1.連続の式(質量保存則)
連続の式は質量保存則の意味を持ち、流体内に固定された体積領域Vに着目して、Vの質量変化量=Vの表面を通過した流体の質量
であることを表したものです。
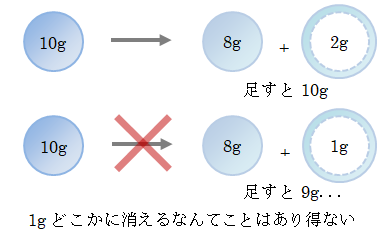
図3.1-1 質量保存
ここで、連続の式を数式化します。流体の密度を\( \rho \)、流速ベクトルを\( \boldsymbol{v} \)、Vの面素ベクトル(1.4節参照)を\( d \boldsymbol{S} \)とするとき、Vの単位時間あたりの質量変化と、そこから流出する単位時間当たりの質量はそれぞれ
- 体積領域Vの質量変化= \( \displaystyle -\frac{\partial}{\partial t} \int \rho dV \)
- 体積領域Vから流出する単位時間あたりの質量= \( \displaystyle \oint \rho \boldsymbol{v} \cdot d \boldsymbol{S} \)
になります。質量が保存するためにはこれらが等しくなければなりません。
\[
\displaystyle
-\frac{\partial}{\partial t} \int \rho dV
=
\int \mathrm{\rho \boldsymbol{v}} dV
\]
この右辺の面積分はガウスの定理により体積積分に書き直せるので、
\[
\displaystyle
-\frac{\partial}{\partial t} \int \rho dV
=
\int \mathrm{div}(\rho \boldsymbol{v}) dV
\\
\Leftrightarrow
\int
\left\{
\frac{\partial \rho}{\partial t} + \mathrm{div}(\rho \boldsymbol{v})
\right\}
dV
=
0
\]
が得られます。このとき、Vは任意なので被積分関数は恒等的に0であり、
\[
\frac{\partial \rho}{\partial t} + \mathrm{div}(\rho \boldsymbol{v}) = 0
\]
この(3.1-1)式を連続の式と呼び、左辺第二項の\( \rho \boldsymbol{v} \)を質量流束密度と呼びます。
(流束という概念は連続の式でも出てくるように、流体では非常に重要な意味を持ちます。 流束の詳細については別途後述します。)
3.2.流体の運動方程式
流体といえど、ニュートンの運動の法則は成り立ちます。 ここでは流体の運動方程式の基本形を導出します。3.2.1.ラグランジュ的導出
ニュートンの運動の第二法則(運動量保存則):物体の運動の変化はその物体に働く力に比例し、力の働く向きに生じる、は質点の質量\( m \)、速度\( \boldsymbol{v} \)、運動量ベクトル\( \boldsymbol{p} \)、力ベクトル\( \boldsymbol{F} \)、を用いて次のように表せます。\[
\frac{d \boldsymbol{p} }{dt} = m \frac{d \boldsymbol{v} }{dt} = \boldsymbol{F}
\tag{3.2.1-1}
\]
質点系で言えば
\[
\sum_i \frac{d \boldsymbol{p_i} }{dt}
=
\sum_i m_i \frac{d \boldsymbol{v_i} }{dt}
=
\boldsymbol{F}
\tag{3.2.1-2}
\]
となります。これらはよく知られる運動方程式です。
ただし、質点系の質量\( \sum m_i \)は一定、つまり系の質量は保存されることに注意します。
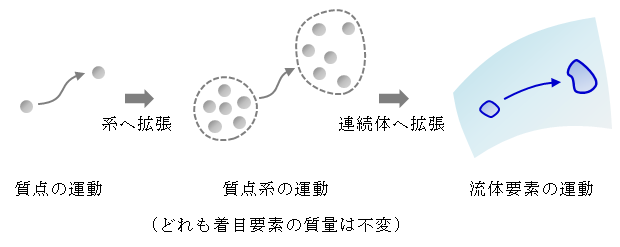
ここで流体の運動に移ります。
流体内のある体積領域Vに着目します。 Vの運動はその体素dV(1.4節参照)に分割した各要素の運動量をV全体で積分すればよく、
\[
\boldsymbol{p}
=
\int \rho \boldsymbol{v} dV
\tag{3.2.1-3}
\]
で定まります。
このとき体素dVは質点系の質点に該当します。
そのため、質点系の運動方程式(3.2.1-2)を参考にすれば、流体の運動に伴ってdVは変化してもその質量\( \rho dV \)は変化しません。
この点を考慮した上でVの運動量変化をみると、
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt}
& =
\frac{d}{dt} \int \rho \boldsymbol{v} dV
\\
& =
\int
\left\{
\rho \frac{d \boldsymbol{v}}{dt} + \boldsymbol{v}\frac{d}{dt}(\rho dV)
\right\}
\\
& =
\int \rho \frac{d \boldsymbol{v}}{dt}dV
\end{align}
\tag{3.2.1-4}
\]
となります。
ここでVに作用する力\( \boldsymbol{F} \)を単位体積当たりの力\( \boldsymbol{f} \)で表せば
\[
\boldsymbol{F}
=
\int \boldsymbol{f} dV
\tag{3.2.1-5}
\]
となって、
\[
\int \rho \frac{d \boldsymbol{v}}{dt}dV
=
\int \boldsymbol{f} dV
\]
\[
\Leftrightarrow
\int
\left\{
\rho \frac{d \boldsymbol{v}}{dt} - \boldsymbol{f}
\right\}
dV
=
0
\tag{3.2.1-6}
\]
が得られます。Vは任意なので被積分関数は恒等的に0であり、
\[
\rho \frac{d \boldsymbol{v}}{dt} = \boldsymbol{f}
\tag{3.2.1-7}
\]
が得られ、この式が流体の運動方程式の基本形になります。
ただしこの表現方法はラグランジュ的なのでオイラー表現に書き直します。
\( \boldsymbol{v} \)は\( t,x,y,z \)の関数なので、その完全微分形(1.5.2節参照)は
\[
d \boldsymbol{v}
=
\frac{\partial \boldsymbol{v}}{\partial t}dt
+ \frac{\partial \boldsymbol{v}}{\partial x}dx
+ \frac{\partial \boldsymbol{v}}{\partial y}dy
+ \frac{\partial \boldsymbol{v}}{\partial z}dz
\]
となります。よって両辺をdtで割れば
\[
\begin{align}
\frac{d \boldsymbol{v}}{dt}
& =
\frac{\partial \boldsymbol{v}}{\partial t}
+ \frac{\partial \boldsymbol{v}}{\partial x}\frac{dx}{dt}
+ \frac{\partial \boldsymbol{v}}{\partial y}\frac{dy}{dt}
+ \frac{\partial \boldsymbol{v}}{\partial z}\frac{dz}{dt}
\\
& =
\frac{\partial \boldsymbol{v}}{\partial t}
+
(
\frac{\partial \boldsymbol{v}}{\partial x},
\frac{\partial \boldsymbol{v}}{\partial y},
\frac{\partial \boldsymbol{v}}{\partial z}
)
\cdot
\left(
\begin{array}{c}
v_x
\\
v_y
\\
v_z
\end{array}
\right)
\\
& =
\frac{\partial \boldsymbol{v}}{\partial t}
+ (\boldsymbol{v} \cdot \mathrm{grad})\boldsymbol{v}
\end{align}
\]
となり、(3.2.1-7)式に代入してオイラー表記の運動方程式が得られます。
\[
\rho \frac{\partial \boldsymbol{v}}{\partial t}
+
\rho( \boldsymbol{v} \cdot \mathrm{grad} )\boldsymbol{v}
=
\boldsymbol{f}
\tag{3.2.1-8}
\]
3.2.2.オイラー的導出
ここではニュートンの運動の第二法則に従った上で、流体内に固定した領域Vの運動量変化から運動方程式の導出を試みます。 結果は当然前節と同じになります。 Vの運動量の時間変化は\[
\frac{\partial \boldsymbol{p}}{\partial t}
=
- \int \frac{\partial \rho \boldsymbol{v}}{\partial t} dV
\tag{3.2.2-1}
\]
になります。
この運動量変化を与える要因に次の二つがあります。
(1)領域Vに働く外力(流体が流出する方向を正とします)
\[
-\int \boldsymbol{f} dV
\]
(2)Vから流出する運動量 = Vの表面を通過する運動量
\[
\int (\rho \boldsymbol{v}) \cdot \boldsymbol{v} d \boldsymbol{S}
=
\int \mathrm{grad}(\rho \boldsymbol{v} \otimes \boldsymbol{v})dV
\]
成分表示すれば(ダイアド積(1.5.1節参照)になじみがない場合)
\[
\int (\rho \boldsymbol{v}) \cdot \boldsymbol{v} d \boldsymbol{S}
=
\int \frac{\partial \rho v_i v_j}{\partial t} dV
\]
\[
- \int \frac{\partial \rho \boldsymbol{v}}{\partial t} dV
=
-\int \boldsymbol{f} dV
+
\int \mathrm{grad}(\rho \boldsymbol{v} \otimes \boldsymbol{v})dV
\]
\[
\Leftrightarrow
\int \left\{
\frac{\partial \rho \boldsymbol{v}}{\partial t}
- \boldsymbol{f}
+ \mathrm{grad}(\rho \boldsymbol{v} \otimes \boldsymbol{v})
\right\}
dV
\tag{3.2.2-2}
\]
Vは任意なので被積分関数は恒等的に0であり、
\[
\frac{\partial \rho \boldsymbol{v}}{\partial t}
+
\mathrm{grad}(\rho \boldsymbol{v} \otimes \boldsymbol{v} )
=
\boldsymbol{f}
\tag{3.2.2-3}
\]
または成分表示で
\[
\frac{\partial \rho v_i}{\partial t}
+
\frac{\partial (\rho v_i v_j)}{\partial x_j}
=
f_i
\tag{3.2.2-4}
\]
となります。
ところで、(3.2.1-8)式も(3.2.2-4)式もどちらも流体の運動方程式ですが、同じ形をしていません。
それについては(3.2.2-4)式に連続の式を適用することで(3.2.1-8)式が導出でき、その結果これらは同じ式であることが証明されます(計算は割愛します)。


