連続体力学
2.3.ひずみテンソル
2.3.1.ひずみテンソルの定義
前節の図(2.2.2-1)について、引き続き考えていきます。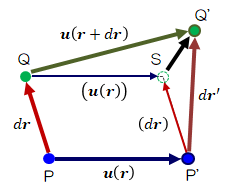
図2.2.2-1 物体の変形に伴う変位
物体の変形は変位だけでなく、変位に伴う物体内の各点間距離の変化もみる必要があります。 そこでP'Q'間距離とPQ間距離の差を求めるために、(2.2.2-2)式の両辺を二乗します。
\[
\begin{align}
|d \boldsymbol{r'} | ^2
&= |d \boldsymbol{r} | ^2
+ 2d \boldsymbol{r} \cdot \frac {\partial \boldsymbol{u}
( \boldsymbol{r} )}{\partial \boldsymbol{r}} d\boldsymbol{r}
+ \left(
\frac {\partial \boldsymbol{u} ( \boldsymbol{r} )}{\partial \boldsymbol{r}} d\boldsymbol{r}
\right) ^ 2
\\
&= \delta_{ij} dx_i dx_i
+ 2 dx_i \frac{\partial u_i}{\partial x_j} dx_j
+ \left( \frac {\partial u_k}{\partial x_j} dx_j \right)^2
\end{align}
\]
テンソルの総和の規約(1.3.1節参照)の性質から
\[
\begin{cases}
\displaystyle
2 dx_i \frac{\partial u_i}{\partial x_j} dx_j
= dx_i \frac{\partial u_i}{\partial x_j} dx_j + dx_j \frac{\partial u_j}{\partial x_i} dx_i
\\
\displaystyle
\left( \frac {\partial u_k}{\partial x_j} dx_j \right)^2
= \left( \frac {\partial u_k}{\partial x_i} dx_i \right)
\left( \frac {\partial u_k}{\partial x_j} dx_j \right)
= \frac {\partial u_k}{\partial x_i} \frac {\partial u_k}{\partial x_j} dx_i dx_j
\end{cases}
\]
とできるので、
\[
|d \boldsymbol{r'} | ^2 - |d \boldsymbol{r} | ^2
= \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}
+ \frac {\partial u_k}{\partial x_i} \frac {\partial u_k}{\partial x_j} \right) dx_i dx_j
\tag{2.3.1-1}
\]
となります。ここで
\[
\epsilon _{ij}
= \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}
+ \frac {\partial u_k}{\partial x_i} \frac {\partial u_k}{\partial x_j} \right)
\tag{2.3.1-2}
\]
は二階のテンソルになります。
これは物体が変形を受けたときの長さ素の変化、つまり\( |d \boldsymbol{r} | ^2 \)から\( |d \boldsymbol{r'} | ^2 \)の変化を決めるもので、ひずみテンソルと呼びます。
ひずみテンソルの単位は[距離÷距離]のため無単位です。
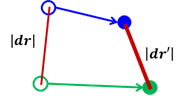
図2.3.1-1 長さ素の変化
また、ひずみテンソルは(2.3.1-2)式のiとjをひっくり返しても全く同じ式になるので対称テンソルです。
\[
\epsilon _{ij} = \epsilon _{ji}
\]
物体の変形を扱う場合、通常その変位は微小である場合が多く、ひずみテンソルの二次の項を無視して次のように近似します。
\[
\epsilon _{ij}
= \frac{1}{2}
\left(
\frac {\partial u_j}{\partial x_i} + \frac {\partial u_i}{\partial x_j}
\right)
\tag {2.3.1-3}
\]
この式をひずみテンソルとして扱うのが一般的です。
ただし、薄板や細長い棒の変形ではこの近似が使えなくなります。
2.3.2.ひずみテンソルの意味
一般にテンソルは対称テンソルと反対称テンソルに分解できるので、変形テンソルもそれに従います。\[
\begin{align}
\frac {\partial u_j}{\partial x_i}
&= \frac{1}{2} \left( \frac {\partial u_j}{\partial x_i} + \frac {\partial u_i}{\partial x_j} \right)
+ \frac{1}{2} \left( \frac {\partial u_j}{\partial x_i} - \frac {\partial u_i}{\partial x_j} \right)
\\
&= \epsilon_{ij} + \Omega_{ij}
\end{align}
\tag {2.3.2-1}
\]
このとき、\( \epsilon_{ij} \ \)は対称テンソル、\( \Omega_{ij} \ \)は反対称テンソルになります。
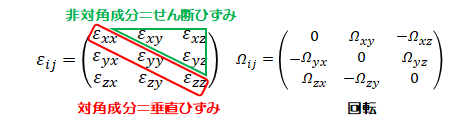
\[
\begin{eqnarray}
\epsilon_{ij}
=
\left(
\begin{array}{ccc}
\epsilon_{xx} &
\epsilon_{xy} &
\epsilon_{xz} \\
\epsilon_{yx} &
\epsilon_{yy} &
\epsilon_{yz} \\
\epsilon_{zx} &
\epsilon_{zy} &
\epsilon_{zz}
\end{array}
\right)
\quad
\Omega_{ij}
=
\left(
\begin{array}{ccc}
0 &
\Omega_{xy} &
-\Omega_{xz} \\
-\Omega_{yx} &
0 &
\Omega_{yz} \\
\Omega_{zx} &
-\Omega_{zy} &
0
\end{array}
\right)
\end{eqnarray}
\]
このとき、対称テンソル\( \epsilon_{ij} \ \)はひずみテンソル(2.3.1-3)式と一致します。
また、詳細は後述しますが反対称テンソル\( \Omega_{ij} \ \)を回転テンソルと呼びます。
ここからは、ひずみテンソルと回転テンソルの持つ意味について見ていくことにします。 なお、分かりやすく表現するために、xy平面内の変形に着目して説明します。
(1)伸縮ひずみ
xy平面内の変形に対するひずみテンソルの対角成分は以下のとおりです。\[
\epsilon_{xx} = \frac {\partial u_x}{\partial x}
、
\epsilon_{yy} = \frac {\partial u_y}{\partial y}
、
\epsilon_{zz} = 0
\]
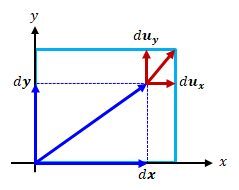
図2.3.2-1 ひずみテンソルの対角成分
\( \epsilon_{xx} \ \)はx軸方向の、\( \epsilon_{yy} \ \)はy軸方向の単位長さあたりの変位量を表しています、 例えば\( \epsilon_{xx} >0 \ \)なら着目要素は伸び、\( \epsilon_{xx} <0 \ \)なら縮むことになります。 つまり、ひずみ\( \epsilon_{xx} \ \)は伸縮率の意味を持ち、垂直ひずみまたは伸縮ひずみと呼びます。(2)せん断ひずみと回転
ひずみテンソル\( \epsilon_{ij} \ ( i \neq j ) \)と回転テンソル\( \Omega_{ij} \ ( i \neq j ) \)の非対角成分について見ていきます。 下図のように角度\( \theta_x 、\theta_y \)をとると、微小変形を前提としているので、ひずみ成分と角度の関係を定義できます。\[
\begin{eqnarray}
\begin{cases}
\theta_x
= \displaystyle
\tan^{-1} \frac {\partial u_y}{\partial x} \simeq \frac {\partial u_y}{\partial x}
\\
\theta_y
= \displaystyle
\tan^{-1} \frac {\partial u_x}{\partial y} \simeq \frac {\partial u_x}{\partial y}
\\
\end{cases}
\quad
\rightarrow
\quad
\begin{cases}
\epsilon_{xy}
= \displaystyle \frac{1}{2} ( \theta_x + \theta_y )
\\
\Omega_{xy}
= \displaystyle \frac{1}{2} ( \theta_x - \theta_y )
\end{cases}
\end{eqnarray}
\tag {2.3.2-3}
\]
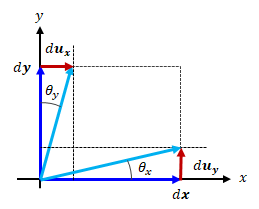
図2.3.2-3 非対角成分の関係図
\( \theta_x 、\theta_y \)の関係によって以下の三つに場合分けします。i)\( \theta_x = - \theta_y \)の場合
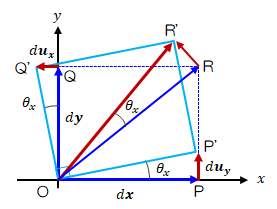
図2.3.2-4 回転
着目要素の形状(長方形)は維持され(∠POQ = ∠P'OQ' = 90deg)、変形は生じません。 また、対角上の点Rの変位点R'はOR線上にないので、着目要素には角度\( \theta_x)の剛体的な回転が生じています。 このとき\( \epsilon_{xy} 、\Omega_{xy} \)は次のようになります。\[
\epsilon_{xy} = 0、
\Omega_{xy} = \theta_x
\]
この結果から、反対称テンソルが回転テンソルであることが説明できます。
ii)\( \theta_x = \theta_y \)の場合
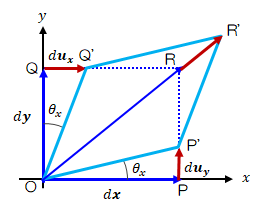
図2.3.2-5 せん断変形
着目要素は長方形(∠POQ= \( \pi / 2 \))から平行四辺形(∠P'OQ' \( = \pi / 2 - 2 \theta_x \) )に変形してひしゃげています。 この変形をせん断変形またはずれ変形と呼び、角度変化\( \theta_x \)をずれ角と呼びます。 このとき、対角上の点RはOR線上で変位するので、着目要素に回転は生じません。 この場合、\[
\epsilon_{xy} = \theta_x、
\Omega_{xy} = 0
\]
となって、ひずみテンソルの非対角成分をせん断ひずみと呼びます。
iii)\( | \theta_x | \neq | \theta_y | \)の場合
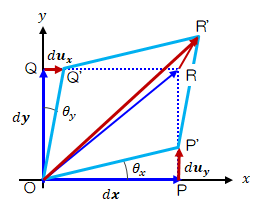
図2.3.2-6 ずれ変形と回転
着目要素の形状は長方形→平行四辺形に変形してひしゃげています。 また、対角上の点Rの変位点R'はOR線上にありません。 従って、このケースでは着目要素に変形と回転が同時に作用することになります。変形によるずれ角は\( ( \theta_x + \theta_y ) / 2 \)になります( ∵ ∠P' OQ' \( = \pi/2-( \theta_x + \theta_y ) \) )。 回転は∠ROR'を求めることになります。 回転を含むずれ角が\( \theta_x \)であるのに対し、純粋なずれ角は\( ( \theta_x + \theta_y ) / 2 \)であることから、回転に用いられる角度は\( ( \theta_x - \theta_y ) / 2 \)になります。
\[
\theta_x - \frac{1}{2} ( \theta_x + \theta_y ) = \frac{1}{2} (\theta_x -\theta_y )
\tag{2.3.2-6}
\]
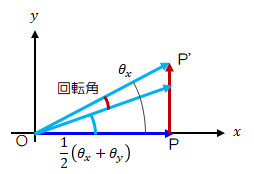
図2.3.2-7 回転角
以上により、\( \epsilon_{xy} 、\Omega_{xy} \)は次のようになります。\[
\epsilon_{xy} = \theta_x、
\Omega_{xy} = 0
\]
これらの結果、ひずみテンソルの対角成分は伸縮、非対角成分はせん断、回転テンソルは回転を表すことになります。
2.3.3.ひずみテンソルの対角化
ひずみテンソルは対称テンソルのため対角化できます。 この対角化は座標変換に他なりませんので、物体の性質になんら影響を与えるものではありません。 この座標変換によるテンソルの対角化を主軸変換と呼び、それぞれの座標軸を主軸と呼びます (主軸変換に対する操作はここでは割愛します)。主軸変換後の対角化したひずみテンソルを次のように表します。
\[
\epsilon_{ij}
=
\begin{eqnarray}\left(
\begin{array}{ccc}
\epsilon_{xx} &
0 &
0 \\
0 &
\epsilon_{yy} &
0 \\
0 &
0 &
\epsilon_{zz}
\end{array}
\right)\end{eqnarray}
\tag{2.3.3-1}
\]
このときせん断ひずみ\( \epsilon_{ij} \ ( i \neq j ) \)はすべて0になるため、物体の変形は主軸方向の垂直ひずみによる伸長のみとなります。
このとき(2.3.1-1)式は
\[
|d \boldsymbol{r'} | ^2
= dx_i ^2 + 2 \epsilon_{ij} dx_i dx_j
= ( 1+ 2 \epsilon_{ij} ) dx_i^2
\tag{2.3.3-2}
\]
と書き換えられ、\( dx_1 、dx_2 、dx_3 \)はそれぞれ直交しているので独立項として扱えます。
従って各主軸方向の長さの変化は
\[
dx_i = \sqrt{ 1 + 2 \epsilon_i \ } dx_i
\]
となり、各主軸方向の相対伸びは次のように表せます。
\[
\frac { dx_i'- dx_i }{ dx_i} = \sqrt{ 1 + 2 \epsilon_i \ } - 1
\tag{2.3.3-3}
\]
物体の変形が微小な場合、相対伸びは次のように近似できます。
\[
\sqrt{ 1 + 2 \epsilon_i \ } \simeq \sqrt{ (1 + \epsilon_i)^2 \ } = 1 + \epsilon_i \\
\leftrightarrow
\sqrt{ 1 + 2 \epsilon_i \ } - 1 \simeq \epsilon_i
\tag{2.3.3-4}
\]
その結果、物体の相対伸びは主軸方向のひずみテンソルに等しいことが分かります。
\[
\frac { dx_i'- dx_i }{ dx_i} = \epsilon_i
\tag{2.3.3-5}
\]
次に物体の体積素片\( dV \)に着目し、変形後の\( dV' \)を求めます。
今、ひずみテンソルの主軸を用いて、
\[
dV = dx_1 dx_2 dx_3
\tag{2.3.3-6}
\]
で表せます。同様に物体の変形後については
\[
dV' = ( 1 + \epsilon_1 ) dx_1 ( 1+ \epsilon_2 ) dx_2 ( 1 + \epsilon_3 ) dx_3
\tag{2.3.3-7}
\]
となりますが、\( \epsilon_{ii} \)は微小量のため2次以上の項を無視して、
\[
\begin{align}
dV'
& \simeq ( 1 + \epsilon_1 + \epsilon_2 + \epsilon_3 ) dx_1 dx_2 dx_3
\\
& = ( 1 + \epsilon_1 + \epsilon_2 + \epsilon_3 ) dV
\end{align}
\tag{2.3.3-8}
\]
の関係が得られます。
ところで、テンソルの対角和はテンソル不変量(座標系によらず不変)であり、非対角成分を含むテンソルの場合でも一定の値を取ります。
従って、物体の変形に伴う体積変化率は、座標系に依らず一定となり、
\[
\frac { dV'- dV }{ dV } = \epsilon_{11} + \epsilon_{22} + \epsilon_{33}
\tag{2.3.3-9}
\]
テンソルの対角和は体積ひずみとしての意味を持ちます。
またこの結果からせん断ひずみのみの場合、対角和は0であるから物体の変形に伴う体積変化はありません。
2.4.変形速度テンソル
これまでは変形に伴う時間について考慮してきませんでした。 流体等動的な変形を扱う場合は、変形の起こる速さ=変形速度を考慮に入れる必要があります。 そこで前々節の図(2.2.2-1)について、再度考えていきます。物体内各点の変形速度\( v \)は
\[
v = \frac{d \boldsymbol{u} ( \boldsymbol{r} ) }{dt}
\]
で表せます。そこで、変形テンソルを時間で微分すると、
\[
\frac{d}{dt} \left( \frac { \partial \boldsymbol{u} ( \boldsymbol{r}) }{ \partial \boldsymbol{r} } \ \right)
=\frac { \partial }{ \partial \boldsymbol{r} } \left( \frac{d \boldsymbol{u} ( \boldsymbol{r})}{dt} \ \right)
=\frac { \partial \boldsymbol{v} }{ \partial \boldsymbol{r} }
= \nabla \boldsymbol{v}
\tag{2.4-1}
\]
2.2節で見た通り変形速度ベクトル\( v \)の勾配になっているので、二階のテンソルになります。
この\( \nabla v \)を変形速度テンソルと呼びます。
変形速度テンソルについては、単位時間当たりの変位が変形速度\( v \)に等しいことから、変形テンソルの\( u \)を\( v \)に単に置き換えればよいということが直感的にわかります。
この流れに従い、変形速度テンソルと同様にひずみ速度テンソルも定義できます。
\[
\begin{align}
\frac { d \epsilon_ij }{ dt}
&= \frac {1}{2} \left( \frac{ \partial v_j }{ \partial x_i}
+ \frac{ \partial v_i }{ \partial x_j}
+ \frac{ \partial v_k }{ \partial x_j}\frac{ \partial v_k }{ \partial x_j}\right)
\\
&\simeq \frac{1}{2}
\left( \frac{ \partial v_j }{ \partial x_i} + \frac{ \partial v_i }{ \partial x_j} \right)
\end{align}
\tag{2.4-2}
\]
また、回転テンソルにあたる変形速度テンソルの反対称テンソルは渦度と呼び、連続体の自転を渦とみてその強さを
\[
\omega_{ij}
= \frac { d \Omega_{ij} }{dt}
= \frac{1}{2} \left( \frac{ \partial v_j }{ \partial x_i} - \frac{ \partial v_i }{ \partial x_j} \right)
\tag{2.4-3}
\]
で表します。渦度の詳細については流体力学で見ていくことにします。


