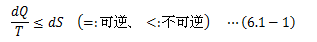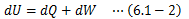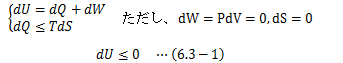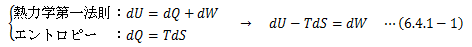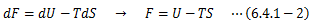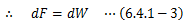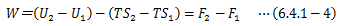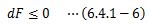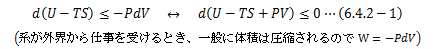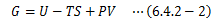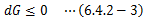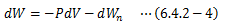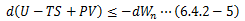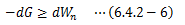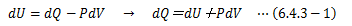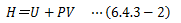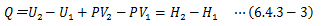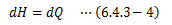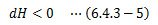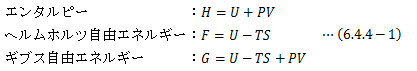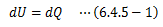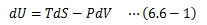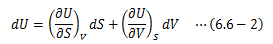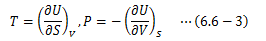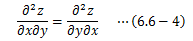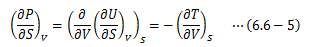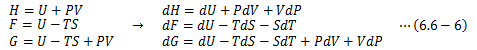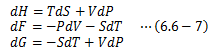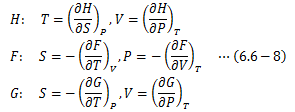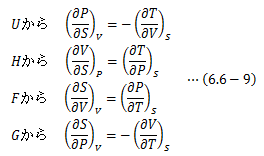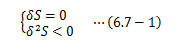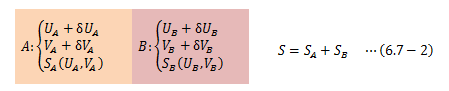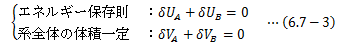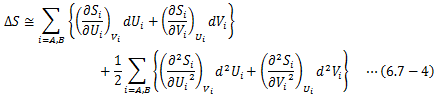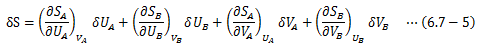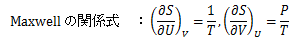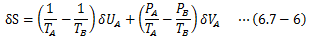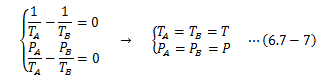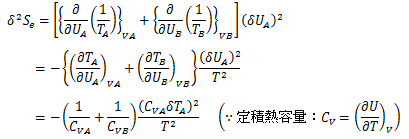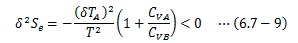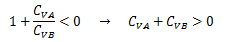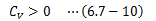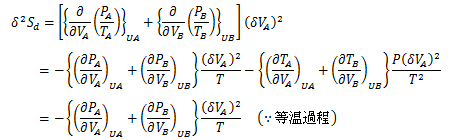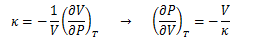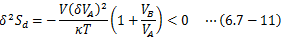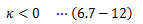6．極値原理

6．1．極値原理とは？

自然現象は一般に、 ある量が最小（極小）または最大（極大）になる方向へ進みます。 これを極値原理と呼びます。 光の屈折に関する“フェルマーの原理”や、（解析）力学における “最小作用の原理”は極値原理をもとに理論構築がなされ、その正しさが公に認められています。
熱力学においても、この極値原理に従い状態変化が進行します。 それを表す元となるのがエントロピーの不等式とエネルギー保存式です。 エントロピーの不等式はは自発的な状態変化の方向を規定するものです。

またエネルギー保存式は、系が熱と仕事を受け取るときを“正”としたとき、 系の内部エネルギー増加量を次式で規定するものです。

ただし、本章で対象とする系は孤立系または閉鎖系とします。

• 孤立系：外界とエネルギーや物質の交換を一切行わない。
• 閉鎖系：外界とエネルギー交換は行うが、物質の交換は一切行わない。

6．2．エントロピー増大則

断熱系のエントロピーは、（6.1－1）式にdQ＝0を代入した次式を満たします。

この式は、断熱系の自発的な状態変化はエントロピーが増大する方向に進むことを意味します。 これをエントロピー増大則と呼びます。
さて、断熱系のエントロピー増大則が重要なわけは、今着目している系が断熱でないとしても、 それに非力学的作用を与えるものまでを含めて系を考えれば、いずれは断熱系が得られるはずである、 と考えられるからです。 現在の人間が想定できる範囲で最大の系は宇宙であり、現段階では宇宙のエントロピーは増大し続けるはずだ、 と主張することができると考えられています。 熱力学第一法則がエネルギー保存を表すのに対して、熱力学第二法則はエントロピー増大を表す、とするのが一般的です。

6．3．最小エネルギー則

等積等エントロピー過程（S、V一定）の系は、熱力学第一法則とエントロピーの不等式から次式を満たします。

これは、 系の等積等エントロピー変化は系の内部エネルギーを最小（極小）にする方向へ進む ことを意味します。 これを最小エネルギー則と呼びます。

6．4．熱力学ポテンシャル

これまでは、断熱系あるいは等積等エントロピー系についての極値原理を見てきました。 しかし、実際に生じる状態変化は

1. 等温
2. 等温等圧
3. 等圧

等、断熱以外の条件下で行われる場合が多々あります。
そこで本章では、これらの条件下で生じる自発的変化が、熱力学関数を新たに定義し、 それらが極値原理に従うことについて見ていくことにします。

6．4．1．自由エネルギー

ここでは等温変化を考えます。 等温可逆過程の系は、熱力学第一法則とエントロピーの定義から次式を満たします。

温度T一定を考慮すれば、上式左辺に対し次のような関数Fが定義できます。

この関数Fをヘルムホルツの自由エネルギー （以降、自由エネルギー）と呼びます。 ここで（6.4.1－1）式を積分すると

となり、系の自由エネルギー変化は外界から受ける仕事と等しく、系の状態のみで決まります。 つまり、自由エネルギーFは状態量になります。
次に不可逆過程を考えると（6.4.1－3）式は次のように表せます。

この式は、系が外界へ仕事を行う場合、系の自由エネルギー減少量よりも少ない範囲でしか仕事を取り出せない、ことを意味します
以上をまとめると、次のようになります。
等温過程の系が外界へ仕事を行う場合、取り出せる仕事は、 不可逆過程では系の自由エネルギー減少量よりも少なく、可逆過程で最大となり、 系の自由エネルギー減少量と等しい
これを最大仕事の原理と呼びます。
さらに等積条件を付与すると、（6.4.1－5）式は

となり、 等温等積過程における状態変化は、系の自由エネルギーを極小にする方向へ進む、 ことがわかります。
ここで自由エネルギーと呼ばれる所以について見ていきます。 （6.4.1－2）式から自由エネルギーFは、 系の内部エネルギー変化から系外部へ支払う熱量を差し引いたものであり、 その分が仕事として自由に使える、という意味を持ちます。 これがFが自由エネルギーと呼ばれる所以です。 また、（6.4.1－5）式のTdSは等温変化を維持するために必要となる熱量で、仕事に使うわけにはいきません。 つまり条件によって束縛されているエネルギーといえます。 このTSを束縛エネルギーと呼びます。

6．4．2．ギブスエネルギー

6.4.1節に等圧条件を付加します。理由は後で説明します。
温度T、圧力P一定を考慮すれば、（6.4.1－2）式は次のように表せます。

このとき、T、Pが一定であることを考慮すれば、次の関数Gが設定できます。

この関数Gをギブスの自由エネルギー（以降、ギブスエネルギー）と呼びます。 ギブスエネルギーGも自由エネルギー同様に考えれば状態量になることがわかります。
さて、このGを（6.4.2－1）式に適用すると、

になります。この式は、 等温等圧過程における状態変化は、系のギブスエネルギーを極小にする方向に進展する ことを表します。
さて、これまで“仕事＝力学的仕事＝系の膨張収縮”として扱ってきましたが、 それ以外にも相変化や電気化学的仕事（化学反応など）、生物学的仕事（光合成など）などが存在します。 状態変化を考える上では、これらのエネルギーも考慮に入れる必要があります。
一般に、化学や生物学におけるサイクルの大半が等温等圧過程として扱われます。 そこで、非力学的仕事を付与することで（6.4.2－3）式がどう変化するか？について見ていきます。 ここでは系が外界から与えられた仕事Wを、力学的仕事（体積変化）と系が行う非力学的仕事－Wn（符号に注意）に分けて

で表します。 すると（6.4.2－1）式は、次のようになります。

結局（6.4.2－3）式は次のように書き換えることができます。

この結果から、 等温等圧過程において、系が行える非力学的仕事は、 系のギブスエネルギーの減少量を超えられない、と言えます。

6．4．3．エンタルピー

系は、外界から与えられた仕事によって一般的に圧縮されます。 つまり体積変化の符号は“－”になります。 このことに注意して熱力学第一法則を表すと、

になります。 ここでP一定を考慮すれば、上式右辺を次の関数Hで定義できます。

この関数Hをエンタルピーと呼びます （昔は“含有熱”といっていたそうです「 EMANの物理学より 」）。 ここで（6.4.3－1）式を積分すると

となり、 エンタルピー変化は、等圧変化における熱の移動そのものであり、 系の状態のみで決まることがわかります。 つまり、エンタルピーHは状態量です。 （6.4.3－3）式は次のようにも表せます。

さてここで閉鎖系、つまり外界とのエネルギー交換のみ可能な系を考えることにします。 このとき、エントロピーはエネルギーではないため外界との交換ができないため、S一定となります。 さらに、エンタルピーHは熱と等価であるため、不可逆過程での関係が次式によって得られます。

これは、 閉鎖系の等圧変化における状態変化は、系のエンタルピーを極小にする方向に進展する ことを表します

6．4．4．熱力学ポテンシャル

状態変化に基づいて定義された自由エネルギーF、ギブスエネルギーG、エンタルピーHは いずれも極値原理に従う熱力学関数であり、同時に状態量を表します。

これらは最小（極小）となることで安定な平衡を与えることから、 力学のポテンシャルとの対比で熱力学ポテンシャル（特性関数）と呼びます。
各熱力学ポテンシャルの定義からわかるように、自由エネルギーによって仕事を、 エンタルピーによって熱量を状態量として扱うことができます。 これにより、過程の経路を気にせずに測定データを熱量や仕事に換算することが可能になります。 つまり、測定データを非常に扱いやすくすることで “算術的メリットを得ること” が熱力学ポテンシャルの本質になります。

6．4．5．Hessの法則

少し話はそれますが、熱と状態量の関係について見ておきます。
一般に実験を行うとき、容器の体積は変化しない場合が多いと思います。 そこで、等積変化を考えます。 このときW＝0となるため、熱力学第一法則は

となります。 つまり、 熱量は等圧変化のときエンタルピー変化と等しく、 等積変化のとき内部エネルギー変化と等しい、ことになります。

このように 等圧変化と等積変化において、熱が過程によらず状態量として扱える ことをHessの法則と呼びます。

6．5．示量変数と示強変数

熱力学では、物質の状態を表すマクロ的な量＝状態量によって理論展開されます。 状態量は平衡状態において定義されますが、局所平衡という概念のもとに、非平衡熱力学でも活用されています。
さて、この状態量は2つの種類に分類されます。

	示量変数	示強変数
定義	系の大きさ、多さに比例する量 （積分的）	系の大きさには依存せず、局所的性質を表す量 （統計あるいは平均的）
例	質量、モル数、体積、内部エネルギー、エントロピーなど	温度、圧力、密度、化学ポテンシャルなど

6．6．マクスウェルの関係式

極値原理を与える熱力学関数U、S、H、F、Gは それぞれ2つの独立な状態量の関数として表すことができます。 このとき、どの状態量を変数として選択するか？によって、 測定や計算が楽になり、後々の負担が軽くなります。 この変数選択について、重要な指針を示すのがマクスウェルの関係式になります。 マクスウェルの関係式は状態量の間に存在する関係を示したものです。
4.9節で述べたように、 状態量変化を決める際の過程を可逆としても任意性を損ないませんので、 内部エネルギー変化は可逆過程のエネルギー保存式を用いることにします。

ここで、内部エネルギーUをエントロピーSと体積Vの関数で表すことにし、 その完全微分形をとると次式が得られます （明らかに（6.6－1）から見て作為的ですが．．．）。

ここで（6.6－1）と（6.6－2）式を比較すると、次の関係が得られます。

ここで、2次偏微分の公式

を用いて（6.6－3）式のT＝～の式をV、P＝の式をSで偏微分します。

この式が意味するところは、以下の通りです。 エントロピーは測定できない量です。 そこで、等積変化でのエントロピーによる圧力変化（上式左辺）を知りたいときは、 断熱変化での体積による温度変化（上式右辺）を測定すれば良いことになります。
これと同様のことを各熱力学ポテンシャルであるエンタルピーH、自由エネルギーF、ギブスエネルギーGで行います。 まずはH、F、Gの完全微分形をとり、

この式の各dUに（6.6－1）式を代入すると、

が得られ、H、F、Gは2つの状態量の関数として表現できていることがわかります。 ここで、各熱力学ポテンシャルの2変数をH(S,P)、F(T,V)、G(T,P)とすると、 内部エネルギーU同様に比較して、次の関係が得られます。

さらに、（6.6－5）が行った処理と同じことを（6.6－4）式を用いて行えば、

といった関係式が得られます。これをマクスウェル（Maxwell）の関係式と呼びます。 （実はここで用いられた変数の対応は、 ルジャンドル変換と呼ばれる方法によって簡単に得ることができます。 ルジャンドル変換については別途 物理数学 のところで話すことにします。）

6．7．平衡の安定性

本節では体積一定の容器に封入された孤立系について考えます。
孤立系はエントロピー増大則dS≧0に支配されています。 これはエントロピーSが極大に向かって自発的な変化が進み、dS＝0、 つまりエントロピーが極大の時点で変化が止まります。 このとき系は平衡状態になります。 以上より、平衡安定性を得るための条件はエントロピーの極大条件そのものであり、以下になります。

ここで系を2つに分割し、それぞれをA、Bとします。 このときA、Bに内部エネルギーUと体積Vの変分を与え、平衡状態からわずかにずらします。 このときの系全体、A、BのエントロピーをU、Vの関数として定義します。

図6.7－1　孤立系の変分

まず、系に対する制約条件（孤立系、全系の体積一定）から次式が得られます。

ここで系全体のエントロピー変化ΔSは、平衡状態近傍のテイラー展開によって次のように表すことができます （ただし、3次以降は微小項として無視します）。

この右辺第一項が1次変分δS、第二項が2次変分δ²Sに相当します。 まず、1次変分δSに着目します。

ここで、Maxwellの関係式

と、系の制約条件（6.7－3）式を（6.7－5）式に適用すると、次式が得られます。

U、Vは独立変数であるため、（6.7－1）式は（6.7－6）式によって恒等的に満足しなければなりません。

つまり、系が平衡状態になるためには、系の温度と圧力が均一でなければならない、 というごく当たり前の結果が得られました。 これは熱力学第0法則と矛盾しません。
次に2次変分δ²Sに着目します。

このとき、上式のように熱安定性の項と、力学的安定性の項の2つに分けることができます。 それぞれは独立に作用するものでるため、個々の影響を独立に見ていくことにします。

以上をまとめると、平衡安定性を得るための条件は以下の通りになります。

1. 系の温度、圧力が均一であること（熱力学第0法則に従う）
2. 定積熱容量CV、等温圧縮率кが共に“正”であること

最後に、これまでの話をル・シャトリエの原理と呼びます。
一般に熱力学的体系において、平衡からわずかにずれた状態になったとき、 系の変化はその原因を取り除く方向に生じる

参考文献

関連ページ