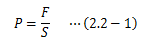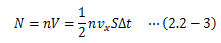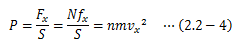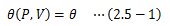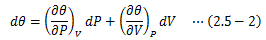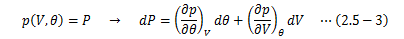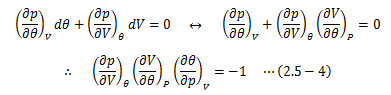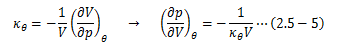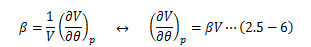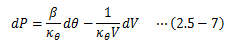熱力学

2．物質の状態量

2．1．熱平衡と状態量

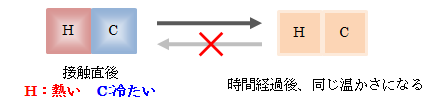
熱さの違う物質を2つ接触させると、2つの熱さは均一化され、その状態から変化しなくなります。

図2.1－1　熱さのつりあい

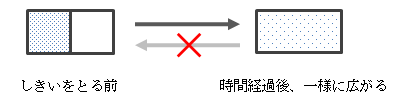
また、真空の容器をしきいによって2つに分け、片側だけに空気を入れた後、しきいをとると空気は容器内に一様に分布し、その状態から変化しなくなります。

図2.1－2　真空膨張

このように、変化しない状態＝つりあい状態を“平衡状態”と呼びます。
一般に、物質が気体、液体、固体のどれであっても、一様かつ等方な場合には体積と圧力で状態が決まるものと考えられています。この体積や圧力といった、物質の状態を決定する量を状態量といいます。熱力学では、この考えを前提に状態量を用いて理論展開されます（温度もこの考えをもとに定義されます）。

2．2．圧力

圧力とは、空間内のある領域に満たされた物質が、膨張・収縮、あるいは物質外部からの力に対してその形状を維持しようとする際に働く単位面積当たりの力です。これは物質の状態を表す量＝状態量になります。

膨張・収縮は領域を仕切る閉曲面の法線方向に生じる変形であるため、圧力もその面の法線方向のみに作用する力となります。
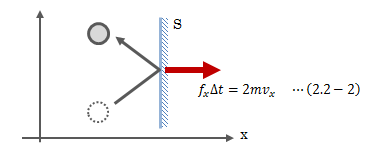
ここでは気体を例にとり、圧力を微視的に見てみます。ある領域に封入されている気体分子はじっとせず動き回っており、面Sに衝突して力積を及ぼしています。

図2.2－1　分子の衝突

このとき、分子と壁の衝突は弾性的（反発係数＝1）とします。図2.2－1は分子1つの動きに着目していますが、実際は多数の分子が面Sに衝突します。 Δt秒間に面Sに衝突する分子の数Nは、単位体積あたりの分子数をn、分子のx軸方向平均速度をv_xとしたとき、次式で求まります。

係数の1/2は次の考えに基づきます。領域内の分子数のうち、半分は＋x方向、残り半分は－x方向に進みます。 Δtの間に衝突する分子は＋x方向に動いているもののみとなるため、1／2が必要になります。以上から、面Sに作用する圧力は

で定まります。このように圧力とは、単位面積に衝突する単位時間あたりの分子の力積平均を衝突する分子の数だけ足し合わせたものと言えます。つまり圧力は、分子1個1個の運動に着目しているわけではなく、分子の平均的な運動によって決まります。

2．3．熱力学第0法則

平衡にない物体を放置すると、次第に平衡状態に移っていくことをごく当たり前のように体験しています。このような平衡体験を公理化します。

系AとBが平衡で、系AとCも平衡なとき、系BとCは平衡である

これを熱力学第0法則と呼びます。
これは結局のところ、系BとCが接触してなくても、系Aを介してそれらの状態が等しいことを確かめることができます。温度計はこの考え方を元に作られています。

2．4．温度

2．4．1．経験的温度と絶対温度

温度とは、 “物質の熱さ／冷たさ”を指し示す量として導入されました。これは、人間の感覚を定量的に示したものと言えます。この温度の定量化、つまり温度目盛りの設定は、物質の熱さ／冷たさ（また圧力の影響）によって膨張／収縮する性質を用いて行います。一般的に日本では温度の単位として摂氏（℃）が用いられます。これは経験的温度といって、物理的に厳密に定義されたものではなく、身近で分かりやすい水の性質を用いて決められたもので、 1気圧の水の氷点（0℃）と沸点（100℃）をもとに定義されています。それに対し、熱力学的に明確に定義された（後述する熱力学第二法則）温度単位としてケルビン（K）があります。この尺度は絶対温度と言い、次のように定義されています。

水の三重点を273.16Kとする
温度間隔1Kは水の三重点温度の1／273.16倍とする

ケルビンと摂氏には次の関係があります。

0K＝－273.15℃
1K＝1℃
T［K］＝θ［℃］＋273.15

2．4．2．温度とは？

ここでは気体を例にとり、温度を微視的に見てみます。
物質は原子や分子から構成されており、それらの動きが大きければ大きいほど運動エネルギーも大きくなります。 1章でも述べたように、同じ圧力環境下に物質が置かれると、温度が高ければ気体に、低ければ固体になることを私たちは経験的に知っています。つまり、物質は分子の運動エネルギーが大きい状態のとき気体で、小さい状態のとき固体であると言えます。
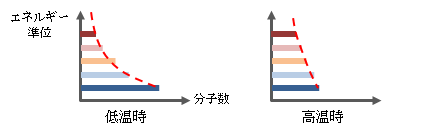
さらに詳しくみていくと、物質を構成する分子のエネルギーはすべて同一ではなく、ある統計的な分布に従っています。これは様々なエネルギー状態にある分子の数を度数分布で表したものと言えます。

図2.4.2－1　物質温度によるエネルギー分布

物質が平衡状態にあっても分子はエネルギー準位を変えながら運動しています。しかし物質全体でみればその度数分布は形を変えずほぼ一定状態を保っており、巨視的にみた物質の状態は一定であると捉えられます。
以上から、温度について次のことが言えます。

温度とは、平衡状態の系を構成する分子のエネルギー分布を決める

つまり、温度はエネルギーと等価と考えることができます。

2．5．状態方程式

2.1節で述べたように熱力学の前提を繰り返すと、物質の状態は圧力Pと体積Vという二つの量によって決まります。また 2.4.1節から、経験的温度θはまさにP、Vで決まる量であり、次の関数で表せることになます。

上式を状態方程式と呼びます。
この関係は温度、圧力、体積のみで行われるものではなく、ある一つの状態量は別の2つの状態量の関数で表せる、と一般化できます。
次に、圧力Pと体積Vは別々の測定方法によって測るため、それぞれは関連のないパラメータ、つまり独立変数として扱えます。このとき、（2.5－1）式は完全微分形をとります。

この式は、温度の微小変化は、体積の微小変化によって生じる温度変化量と、圧力の微小変化によって生じる温度変化量を足し合わせることで決まる、という意味を持ちます。
さて、この状態方程式から等温圧縮率と体膨張率を定義できます。まずは圧力Pを体積Vと温度θの状態方程式として表し、その完全微分形をとります。