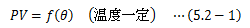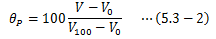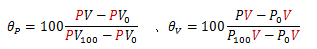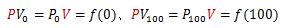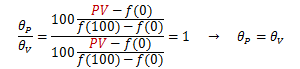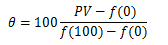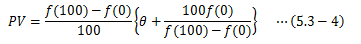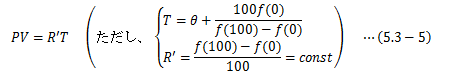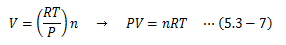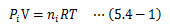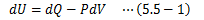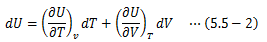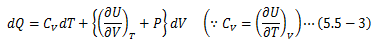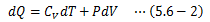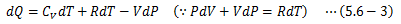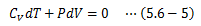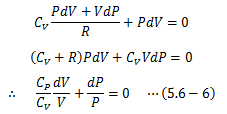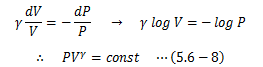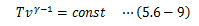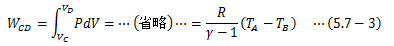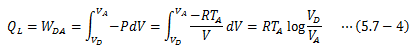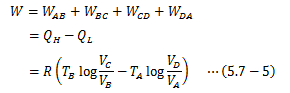5．理想気体

5．1．理想気体とは？

理想気体とは、 気体分子の体積、相互間作用を無視し、さらに化学的変化が起こらない理論上の気体 であり、現実には存在しません。 ただし、実在する気体でも低圧高温状態では理想気体に近い振る舞いをします。

5．2．ボイルの法則

気体の温度θを一定に保つと、気体の圧力Pと体積Vを掛け合わせたものは一定 となることをボイルの法則と呼びます。

上式f(θ)はある温度によって決まる定数で、温度が変われば変わります。 実験結果により、実在する気体ではこの法則からいくらかずれが生じますが、 低圧高温状態にするとボイルの法則によく合致するようになります。 理想気体においては、ボイルの法則を完全に満足します。

5．3．温度と状態方程式

理想気体はボイルの法則に従います。

ここで、理想気体を用いた温度計を作成してみます。 θは摂氏温度とし、水の氷点と沸点の体積と圧力を（V₀、P₀） （V₁₀₀、、P₁₀₀）とします。 まず、圧力P一定にして理想気体の体積変化を測定し、温度θ_Pを次式で定義します。

同様に、体積V一定にして理想気体の圧力変化を測定し、温度θ_Vを次式で定義します。

この2式は次のように変形できます。

このときボイルの法則から

が成り立つので次式が得られます。

これは、θ（つまり経験的温度）が圧力Pであろうと体積Vであろうと同じ値を示すことを意味します。 以上より、任意の温度θに対して次式が成り立ちます。

これをPVについて解き、

次のように定義します。

このTを理想気体温度と言います。 これは実験結果から絶対温度と一致することがわかっています。

次に、 理想気体に同一温度圧力の条件下で、 体積とそこに含まれる分子数は比例関係にある 、とするアボガドロの法則を適用します。 なお、分子数の単位にはモルを用います（1モル＝6.02×10²³個）。 そこでnモルの理想気体に対するアボガドロの法則は、（5.3－5）式から

このRを理想気体定数、（5.3－7）式を理想気体の状態方程式と呼びます。 なお、理想気体定数はR=8.314 J／K molであり、気体の種類によらず一定です。

5．4．分圧の法則

複数の理想気体が混合された系を考えます。 このとき、混合気体の各成分による圧力、つまり分圧は他の成分によらずそれぞれ独立に理想気体に従います。 ある成分をiとしたときの分圧Piは

を満足します。これをダルトンの分圧の法則と呼びます。

5．5．内部エネルギー

ここでは理想気体の内部エネルギーの特徴について見ていきます。
1モルの理想気体に熱力学第一法則を適用します。 理想気体の仕事はその膨張／圧縮のみで決まるので、

また、内部エネルギーをT、Vの関数として表し、その完全微分形をとります。

以上から、次の関係式が得られます。

（ここまでは 3.8節「比熱」の話と同じです。 ただし、C_Vは定積モル比熱とします。） ここで、断熱条件下で実施された“気体の真空膨張実験（ゲイリュサック・ジュールの実験）”において、 気体は仕事をせず、さらにその温度は変化しないという結果が得られました。 この結果を（5.5－3）式へ適用します。

この式から、 理想気体の内部エネルギーは温度のみの関数 で表せることを意味します。

5．6．断熱変化

理想気体の断熱変化はポアソンの方程式

に従います。この式の導出過程をここでは見ていきます。
前節の結果を反映した（5.5－4）式は次のようになります。

ここに状態方程式（5.3－7）式の微分形を上式に代入すると、

となります。 定圧モル比熱C_Pは上式をdP＝0として両辺dTで割ることで得られます。

この式によって、定圧モル比熱と定積モル比熱の差が理想気体定数のみで決まる、という重要な結果が得られました。 今度は、理想気体に断熱変化をさせる場合、dQ＝0であるため（5.6－1）式は

になります。（5.6－3）（5.6－5）式からdTを消去すると、

ここで、比熱比γを以下のように定義します。

比熱比γは実際の気体でほとんど定数をとるため、（5.6－7）式は簡単に積分できます。

この式を理想気体の断熱変化に対するポアソンの方程式と呼びます。 これは次のようにも書き換えることができます。

R＞0であることから

であることがわかります。

5．7．カルノーサイクル

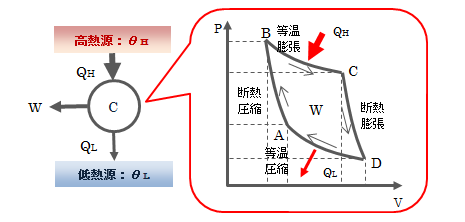
温度が一定に保たれている2つの熱源間で作動する理想気体のカルノーサイクルについて見ていきます。

図5.7－1　カルノーサイクル

以上から、カルノーサイクルが行う仕事Wは次のようになります。

ここで（5.6－8）式から

が得られるので、カルノーサイクルが行う仕事と、受け取る熱量、吐き出す熱量の関係が得られます。

参考文献

関連ページ