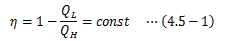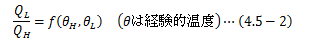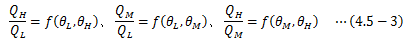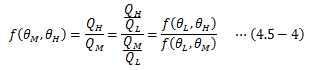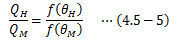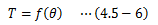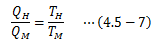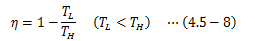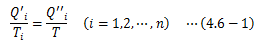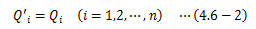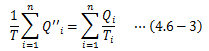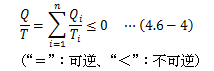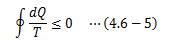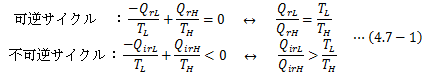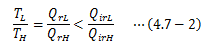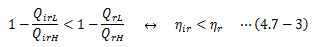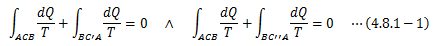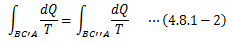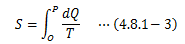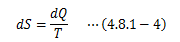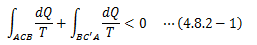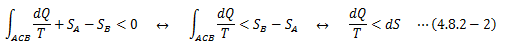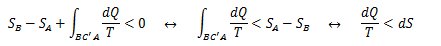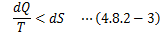4.5.絶対温度
2.4節 で述べた絶対温度の導出過程をここでは見ていきます。前節から、温度の決まった2つの熱源間の任意の可逆サイクルの効率はすべて等しく
で表せるため、熱量比QL/Q
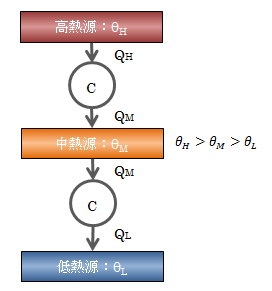
そこで、2つのカルノーサイクルを直列につないだ複合サイクルを考えます。 真ん中の熱源は温度θM一定とするため、熱量の出入りを同じにしておきます。
図4.5-1 直列可逆サイクル
この複合サイクルも可逆になります。 さて、それぞれの可逆サイクルの熱量比は以下のようになります。
この3つの式を組み合わせて次の式を作ることができます。
上式左辺と右辺は恒等的に等しくなるので、右辺にしか含まれないθLには依存しません。 よって、(4.5-4)式は次のように書き換えられます。
f(θ)は経験的温度の1価関数であることから、温度と等価な関数として扱えます。 そこでf(θ)を温度目盛りとして設定しそれをTで表します。
このTについて、 標準状態における水の3重点をT=273.16Kとし、 水の沸点と氷点の温度差を100と決めることで、温度Tの絶対値が決まります。 この温度Tを絶対温度(熱力学的温度)と呼びます。
絶対温度を定義することと(4.5-5)式から、 高熱源から与えられる熱量と低熱源へ与える熱量の比がそれぞれの熱源温度のみで表せることになります。
これにより、可逆サイクルの熱効率は絶対温度TL、THのみで表せることがわかります。
4.6.クラウジウスの不等式
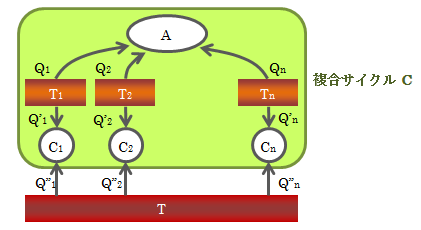
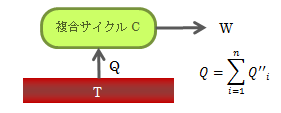
クラウジウスの不等式は、系の状態変化の方向性を決める上で非常に重要な役割を持ちます。まず、下図のような複合サイクルCを考えます。 Ci(i=1,2,…,n)はカルノーサイクル、Tiは熱源、 Aは任意のサイクル(可逆/不可逆どちらでもよい)とし、サイクルが吸収する熱量Qを“+”とします。
図4.6-1 複合サイクル
この複合サイクルCでは熱源Tiの温度が不変になるよう、 カルノーサイクルCiを稼働させるものとします。 前章(4.5-7)式から、各カルノーサイクルの熱源からの熱量比は次式で表せます。
また、熱源Tiの温度は一定に保つため、
も満足する必要があります。 以上よりQ’iを消去して、すべてのiについて足し合わせることで、次式を得ます。
最終的に、複合サイクルCは下図のように単純化できます。
図4.6-2 複合サイクルC簡略図
この複合サイクルCは 図4.3-1ケルビンの原理 と比較すると一目瞭然で、Q>0のときケルビンの原理に反するため、あり得ません。 よって、複合サイクルCの取り得る条件はQ≦0、特に
- Q<0のとき不可逆
- Q=0のとき可逆
これを連続的に記述すれば、
になります。複合サイクルCは可逆サイクル+任意のサイクルで構成されているため、 可逆/不可逆のどちらでも構いません。 以上より、 任意のサイクルが取り得る条件式 をクラウジウスの不等式と呼びます。
4.7.カルノーの定理
カルノーの定理とは、 2つの熱源間に働く任意の可逆サイクルの熱効率は熱源の温度のみで決まり、 あらゆる熱サイクルの中で最大の効率を持つ、というものです。 これは、4.4節か4.6節までの話をまとめた内容に相当します。ここでは、可逆サイクルの熱効率が不可逆サイクルのそれよりも大きいことを証明します。 クラウジウスの不等式を用いて、 2つの熱源(温度TH>TL)間で働く可逆サイクルと不可逆サイクルの熱効率を比較してみます。
(4.6-4)式から可逆/不可逆サイクルにおいて、次の関係が成り立ちます。
よって、
可逆サイクルの熱効率をηr、不可逆サイクルの熱効率をηirとすれば、
となり、 可逆サイクルの熱効率が不可逆サイクルの熱効率よりも大きくなる ことが証明されました。
4.8.エントロピー
エントロピーとは、 乱雑さやでたらめさの尺度を表すもの です。 実際にそのとおりですが、熱力学とどう関連するのかがいまいちよく見えません。 そこで本章では、エントロピーの熱力学からの導出と、統計力学的な見方のさわりだけ見ていこうと思います。4.8.1.エントロピーの定義
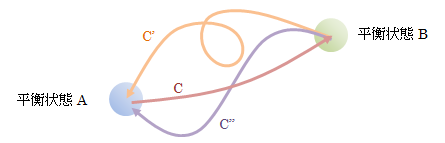
エントロピーは、 可逆過程における状態量として定義されます。 ある系が平衡状態AからBへ移り、再度Aに戻るサイクルを考えます。図4.8.1-1 平衡状態の遷移
このとき、次の2つの経路を考えます。
- AからCを経由してBに移り、C’を経由してAに戻る
- AからCを経由してBに移り、C’’を経由してAに戻る
となり、ここから以下の関係が得られます。
これは 可逆過程の場合、dQ/Tの積分量は経路に依らず、 状態Aと状態Bのみで決まる=状態量 であることを表しています。
そこで、ある基準となる平衡状態Oを選出し(イメージはポテンシャルの基準と同じ)、 任意の平衡状態Pで得られるdQ/Tの積分を関数Sで定義します。
このSを状態Pのエントロピーと呼び、状態量になります。 また、エントロピー変化は微分形で表すことができます。
ここで一つ注意点は、 dS=0のとき2つの状態間に差異がない、つまり平衡状態 を表します。
4.8.2.不可逆過程のエントロピー
前節では可逆過程におけるエントロピーを定義しました。 そこで、本節では不可逆過程におけるエントロピーについて考えます。まずクラウジウスの不等式から次式が得られます。
dQの正負は、外界から系に与えられた熱量を“+”と定義していることに注意します。 経路Cを不可逆、経路C’を可逆とすると、エントロピーの定義から
これは逆で考えても同じ結果になります。
よって、不可逆過程におけるエントロピーは次の関係式を満足しなければなりません。
この式は、 6章 以降で見ていく 状態変化の方向性と安定性を知る上で必要となる関係式です。
4.8.3.エントロピーとは?
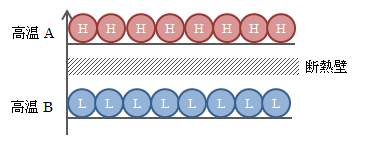
これまでの内容では、エントロピーにいったいどういった意味があるのかが見えてきません。 そこで本節では、ある簡単な例を用いてエントロピーの本質について考えてみます。高温の物体Aと低温の物体Bを接触させると、熱エネルギーの移動によって2つの物体は均一な温度で平衡状態になります。 この状態変化についてミクロな視点で見ていきます。
図4.8.3-1 物体の温度変化
下図は、上図(1)での物体A、Bの分子エネルギー配列を示します。
図4.8.3-2 独立状態のエネルギー分子配列
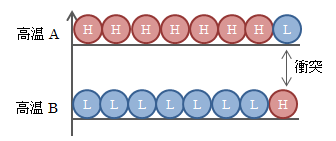
次に、図4.8.3-1(2)の状態に移すと、AとBの境界面で分子のいくつかが衝突します。 分子の衝突が弾性衝突の場合、分子のエネルギー準位はAとBで入れ替わります。
図4.8.3-3 接触直後のエネルギー分子配列
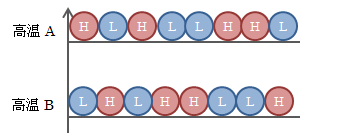
その後時間が経過するにつれ、分子同士の衝突は活発になり、 物体Aと物体Bの分子はエネルギー準位を入れ替えながら状態を変化させていきます。 そして最終的には、様々な分子のエネルギー配列の中で最も確率の高い状態、 つまりそれぞれのエネルギー準位に物体Aの分子と物体Bの分子が同数存在する状態に落ち着きます。
図4.8.3-4 平衡状態のエネルギー分子配列
このように、エネルギーの違う分子がごちゃまぜになった状態が、自発的に生じる状態変化の最終形となります。 ここにエントロピーの本質が現れます。 エントロピーは、 乱雑さやでたらめさの尺度を表すもの として紹介しました。 それはまさにこの分子配列の“乱雑さ”を表現しています。 この内容の詳細は、統計力学で明らかになります。
4.9.状態変化の連結
状態量である内部エネルギーU、エントロピーSなどは、系の状態が決まれば一意に決まります。 そのため、状態遷移によって得られた状態量の変化は、 その過程、つまり可逆/不可逆に関係なく一意に決まります。図4.9-1 状態変化の連結
よって、 状態遷移に可逆過程を用いても過程の任意性は損なわれません。