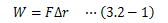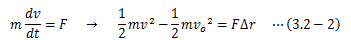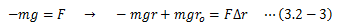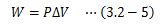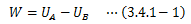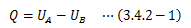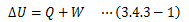3.熱力学第一法則
3.1.準静過程
準静過程とは、 常に系が平衡状態を保ちながら、ゆっくりと変化を進める過程 のことです。 ただし、 準静過程は極限過程であり実現不可能です。 しかしながら、準静過程による理論構築の重要性は、次の理由から明白です。- 実現不可能といえど、近似的に準静過程として扱える事象はいくらでも存在(体温を測る等...)。
- 物理現象の連続性から、準静過程から得られる結論をもとに非準静的な現象についても議論することが可能(局所平衡)。
3.2.仕事
仕事とは力学ですでに定義されており、 物体に外力Fを加えた時、それによって発生する変位Δrとの積で表す量です。仕事は運動方程式を変位で積分することによって得られます。
また、重力場において物体を準静的に動かせば、次式が得られます。
これら2式を次のようにまとめて書いてみます。
この式から、運動エネルギーや位置エネルギーは仕事を介してエネルギーの交換を行っている、つまり、 仕事とはエネルギーの移動形態を表すもの 、と捉えることができます。 この仕事Wは面積Sの絡みから、系の圧力P、体積変化ΔVを用いて書き換えることができます。
なお、仕事の持つ意味については 3.6節に譲ることにします。
3.3.断熱
まず注意しておきたい点は、 断熱を定義するのに“熱”の概念は不要 、ということです。断熱とは、 外界から系に及ぼす影響が、力学的作用のみに限定 される場合のことを指します。 力学的作用とは、例えばピストン壁を押したり、重力やクーロン力等の遠隔力による系の駆動などが挙げられます。 それに対し、炎であぶったり、電熱器で温めたり、光を照射させたりするのは力学的作用にはあたりません。
3.4.熱力学第一法則
本章では、次のステップを踏んで熱力学第一法則の持つ意味について見ていきます。- 断熱系での熱力学第一法則と“内部エネルギー”の定義
- 非断熱系での熱力学第一法則と“熱”の定義
- エネルギー保存則としての熱力学第一法則
3.4.1.断熱系の熱力学第一法則
はじめに力学的な内容しか知らない状態から、熱力学第一法則を見ていくことにします。熱力学第一法則とは、次に示す 経験則を公理化したものです。
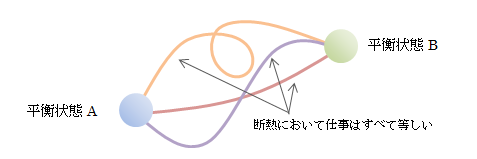
ある系が2つの平衡状態を断熱過程によって移動するときに、 外界から系へ与えられた仕事の総量は移動経路(方法)に依存せず、 2つの平衡状態のみによって決まる
図3.4.1-1 平衡状態の移動
これは言い換えると、2つの平衡状態A、Bはその過程の経路によらずに決まることを表しています。 さて、2つの平衡状態A、Bを表す状態量をUA、UB、 外界から系へ与えられた仕事をWとしたとき、次式で表すことができます。
ここで、UA、UB(以降Uとする)は以下の理由からエネルギーと捉えることができます。
3.4.2.非断熱系の熱力学第一法則
次に、断熱条件を取り払います。系に非力学的な作用を与えても状態変化が生じることを経験的に知っています。 例えば、系を炎であぶる行為がそれにあたります。 この場合系の温度は上昇しますが、外界から系に与えた仕事は0であり、(3.4.1-1)式は成立しません。 そこで、何か別の新しいエネルギーと等価な量が必要となります。 それをQとおくと、(3.4.1-1)式は次のように書き換えられます。
このQを“熱”と呼びます。 熱も仕事同様、エネルギーの移動形態であることがわかります (3.2節参照)。 なお、熱の持つ意味については 3.6節に譲ることにします。
3.4.3.エネルギー保存則
さらに、系には力学的作用と熱の両方を同時に与えることも可能です。 この場合、 外界から系に与えた熱と仕事の和が、系の内部エネルギー変化と等しい 、と言えます。この表現は、まさに高校で習った熱力学第一法則そのものです。 ここで、仕事と熱の扱いに注意が必要です。 内部エネルギーは平衡状態によって一意に決まる量であり、その変化量ΔUも一意に決まりますが、 ΔUを決定する熱Qと仕事Wの組み合わせは無限にあり、それぞれを一意に決めることは出来ません。 つまり、 熱Qと仕事Wは状態量ではない 、ということです。 これらは先に述べたように、 熱も仕事もエネルギーの移動形態を表すもの であることからも明らかです。
また、次の点に注意が必要です。 仕事と熱はエネルギーの移動形態を区別しているだけで、 エネルギーの性質を区別しているのではありません。 よって、仕事によって蓄えられた内部エネルギーと熱によって蓄えられた内部エネルギーは、 いったん蓄えられてしまえば区別はありません。
最後に、孤立系について(3.4.3-1)式を当てはめると、孤立系は外界と物理量の変換を一切しないため、 エネルギーの移動は系内で完結されます。 つまり、 孤立系のエネルギー総量は不変である という主張ができます。 この意味から、 熱力学第一法則はエネルギー保存則である 、ということがわかります。