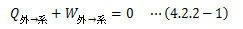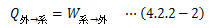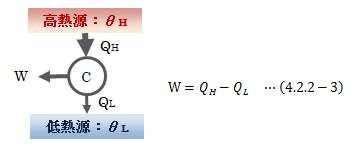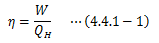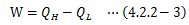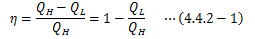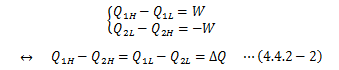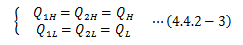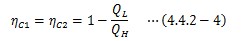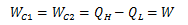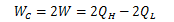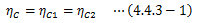4．熱力学第二法則

4．1．可逆過程と不可逆過程

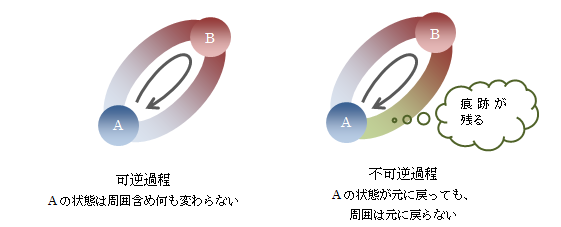
可逆過程とは、 系が状態AからBへ移りまた元の状態Aに戻るとき、 外界に変化が全く残らないようにすることが可能な過程 のことを言います。 それに対し不可逆過程は、可逆過程ではないものと定義されます。

図4.1－1　可逆過程と不可逆過程

現実に起きるすべての現象は不可逆過程になります。 例えば、お湯に氷を入れると水になり、その状態が維持されます。その状態から氷とお湯に戻ることはありません。 このように 不可逆な現象は、ある方向に時間的に発展するが、 その逆は起こらない現象と言えます。
次に、可逆過程の特徴について見てみます。 準静過程は可逆です。 それは、初めの過程とまったく同じ経路を逆向きにたどることができるためです （例えば、周囲に放出されたエネルギーもかき集められます）。 またこの逆の、可逆過程は準静的でもあります。 これは、 非静的な現象は不可逆である という公理化された経験則（熱力学第二法則）をもとに証明されます。

これを反転させると、

以上から、 “可逆過程＝準静的過程” が成り立ちます。

4．2．サイクル

4．2．1．熱機関とサイクル

熱機関とは、 熱によって蓄えられたエネルギーを仕事として利用する装置 です。 熱機関の代表的なものとして、蒸気機関やエンジンなどがあります。 これらは、ピストンやタービンの繰り返し運動、つまり循環運動によって動力を得ています。 1回の循環につき、加熱、冷却、圧縮、膨張など様々な状態変化を経由し、また元の状態に戻ります。 このように、 種々の状態変化を経由して元の状態に戻る過程 をサイクル（循環過程）と呼びます。 熱機関の目的は上述の通り、熱エネルギーから仕事を取り出すことです。 よって熱機関では、 仕事として取り出せるエネルギーの効率が重要 になります。

4．2．2．カルノーサイクル

カルノーサイクルとは、 2つの温度の違う熱源（θ_H＞θ_L）の間で、 高熱源から正の熱量QHをもらい、 低熱源に正の熱量Q_Lを与える可逆サイクル のことを指します。 このとき、作用物質は気体、液体、固体のどれでもかまいません。 カルノーサイクルは可逆ゆえ、その逆のサイクルも成り立ちます。 これを逆カルノーサイクルと言います。
さて、カルノーサイクルが1サイクル行うと元の状態に戻ることから、内部エネルギー変化は0になります。 よって、熱力学第一法則から次式が成り立ちます。

一般に外界から系に正の熱を与えると、その系は膨張（dV＞0）します。 よってこの場合、系は外界に対して“正”の仕事を行うことになり、上式は以下のように書き換えられます。

よって、カルノーサイクルに対して次の定理が成り立ちます。

カルノーサイクルは外界に対して“正”の仕事を行う

図4.2.2－1　カルノーサイクル

4．2．3．任意の可逆サイクル

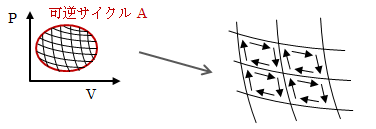
ここでは、 任意の可逆サイクルAがカルノーサイクルの組み合わせによって表せる ことを証明します。
可逆サイクルAが作る閉曲線内を微小な面積素片で分割すれば、全て同一形状の任意の面積素片として扱えます。 それは、テレビの各ピクセルが同じ形状にもかかわらず、画面は任意の形状を表せるのと同じです。

図4.2.3－1　可逆サイクルの分割

そこで、次の理由から微小面積素片を1つのカルノーサイクルと見ることができます。

1. 微小面積は閉曲線に囲まれている（さまざまな状態を経由して元に戻る）
2. 閉曲線は自分以外、つまり外界と接触している（曲線を隣り合う面積素片と共有）
3. 隣り合う微小面積間で熱の移動を考慮できる

さて上図からわかるように、隣り合う微小カルノーサイクルが共有する線上では、同一過程で向きが逆に作用します （カルノーサイクルは可逆ですのでそれが可能です）。 つまり、隣り合う線上では特性の打ち消し合いが生じ、 最終的には微小カルノーサイクルが隣り合わない線の特性のみで決まることになります。 この隣り合わない線こそが可逆サイクルAを示す閉曲線ということになります。
以上より、 任意の可逆サイクルは、無限小のカルノーサイクルの組み合わせによって表せる ことがわかりました。

4．3．熱力学第二法則

熱力学第二法則は、 不可逆に違いないとされる経験的現象を法則 として公理化し、他の現象が不可逆か？可逆か？を判断する材料とします。 これは現象が不可逆になるのは何故か？を説明するものではありません。 熱力学では、この経験則を何も考えず事実として受け入れるしかありません。 熱力学第二法則の表現方法は複数ありますが、それらはすべて等価であり、 どれか一つ正しければ、ほかの表現も正しいことが証明されます。
熱力学第二法則の表現

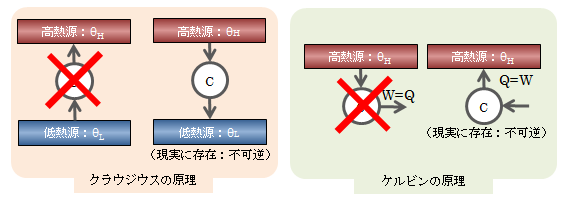
1. 熱が高温から低温へ移る現象は不可逆である（クラウジウスの原理）
2. 仕事が熱に変わる現象は不可逆である（ケルビンの原理）
3. 摩擦により熱が発生する現象は不可逆である

など

図4.3－1　熱力学第二法則の例

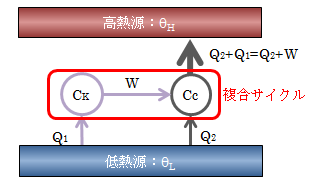
そこで例として、クラウジウスの原理を用いてケルビンの原理が正しいことを、背理法によって証明してみます。 今、ケルビンの原理を否定したサイクルC_Kが存在するものとし、 下図のように2つの熱源間でサイクルC_Kと逆カルノーサイクルC_Cを働かせます。

図4.3－2　ケルビンの原理の証明

このとき、サイクルC_Kが行う仕事Wをすべてもらって 逆カルノーサイクルC_Cは動くものとします。 この複合サイクルでは、低熱源から奪われた熱量がすべて高熱源に移動し、系外部に対しては何も行われていません。 これはクラウジウスの原理に反します。よってケルビンの原理を否定してはなりません。

4．4．熱効率

4．4．1．熱効率の定義

熱効率とは、 系が1サイクル行う間に高熱源から得た熱QHのうち、 どれだけを仕事Wに変換できたか？を割合で示したものです。

これは工業的に非常に興味をそそられるものになりますが、 理論においても状態変化の方向性を特定する上で重要な役割を担います。

4．4．2．カルノーサイクルの効率

カルノーサイクルが行う仕事は

で決まるので、その効率は次のようになります。

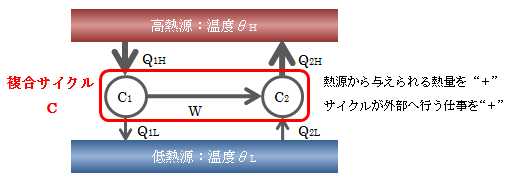
次に、温度の違う2つの熱源（θ_H＞θ_L）の間に、 2つの異なるカルノーサイクルC₁、C₂を働かせた複合サイクルCを考えます。 ただし、C₂は逆カルノーサイクルとし、 C₁が行った仕事をそのまま受け取っては働くものとします。

図4.4.2－1　複合サイクルC

このとき 複合サイクルCが可逆 であることは、C₁、C₂が可逆であることから明らかです。 次に、各カルノーサイクルの熱量と仕事から、次式が得られます。

ここでΔQ＜0、＞0、＝0で場合分けします。

（1）ΔQ＜0のとき

（2）ΔQ＞0のとき

以上より、複合サイクルCがとり得る条件はΔQ＝0、つまり

になります。 以上から、 仕事の等しい2つの異なるカルノーサイクルの熱効率は等しく、 また熱源からの熱移動は一意に決まる ことがわります。

4．4．3．可逆サイクルの熱効率

再度図4.4.2－1に着目します。 今度は逆カルノーサイクルC₂を通常のカルノーサイクルとして働かせて、 複合サイクルCの熱効率を考えます。 すると、カルノーサイクルC₁、C₂とも

であることから、複合サイクルCが外界へ行う仕事は

になります。 このとき、複合サイクルCの熱効率は、カルノーサイクルC₁、C₂と同じになります。

また、2つだけではなく任意のn個に対してもこの関係が維持されることは、容易にわかります。 つまり、 仕事が等しくなくても同じ熱源間で働く任意のカルノーサイクルの熱効率は等しい ことがわかりました。
さらに、任意の可逆サイクルはカルノーサイクルで表現可能であること （4.2.3節）と合わせると、 同じ熱源間に働くすべての可逆サイクルの熱効率は等しい 、と言えます。

参考文献

関連ページ