5.3.正準変換
5.3.1.正準変換
1.1節でみた一般座標から別の座標への変換は、時間を陽に含んでいても成り立ちます。\[
Q_i
=
Q_i(q_1, q_2, \cdots , q_s, t)
\tag{5.3.1-1}
\]
このような変換を点変換と呼びます。
実は、この変換によって得られたQは、本節後半ではもはや座標である必要はなく、単にこの関係式によって縛られた“量”あるいは“変数”として扱うことができます。
これについては後半で触れていくことにします。
ラグランジュ方程式の形はこの点変換に対して不変ですが、これはハミルトン方程式に対しても成り立ちます。 ただし、ラグランジュ方程式の自由度がsである場合に対し、ハミルトン方程式の自由度はその倍の2sになるため、点変換も自由度2sに拡張されます。
\[
\begin{eqnarray}
\left\{ \begin{array}{l}
Q_i
& = &
Q_i(q_1, q_2, \cdots , q_s, p_1, \cdots, p_s, t)
\\
P_i
& = &
P_i(q_1, q_2, \cdots , q_s, p_1, \cdots, p_s,, t)
\end{array} \right.
\end{eqnarray}
\tag{5.3.1-2}
\]
今、変換された量Q、Pを用い、それらを含むハミルトニアンH’(P,Q)によって、ハミルトン方程式(5.1.1-9)式
\[
\begin{eqnarray}
\dot{Q_i}
& = &
\frac{\partial H'}{\partial P_i}
\\
\dot{P_i}
& = &
- \frac{\partial H'}{\partial Q_i}
\end{eqnarray}
\tag{5.3.1-3}
\]
が得られるような変換があるとします。
この変換は方程式の形を不変にとどめるものであり、正準変換と呼びます。
次節では、この正準変換が満足すべき条件について調べることにします。
5.3.2.母関数
5.1.3節で見たように、ハミルトン方程式は最小作用の原理から得られます。\[
\delta \int \left( \sum p_i dq_i - Hdt \right)
=
0
\tag{5.3.2-1}
\]
今、点変換によって得られた量Q、Pがハミルトン方程式を満足する条件を見つけ出そうとしているので、Q、Pにおいても最小作用の原理を満足しなければなりません。
\[
\delta \int \left( \sum P_i dQ_i - H'dt \right)
=
0
\tag{5.3.2-2}
\]
これら二式の間には、座標、運動量および時間の任意関数Fの完全微分だけ異なっても構いません
(1.4節ラグランジアンの不定性参照)。
よって、点変換によるハミルトニアンの条件式は
\[
\sum p_i dq_i - Hdt
=
\sum P_idQ_i - H'dt +dF
\tag{5.3.2-3}
\]
を満足し、このときに得られる関数Fを、変換の母関数と呼びます。
母関数は4s+1個の変数(s個:q,Q,p,P、1個:t)を持つことになりますが、(5.3.1-2)式によって2s個の従属関係を持つことから、結局母関数の変数は2s+1個になります。
さて、(5.3.2-3)式を、母関数を定める形で書き直すと、
\[
dF
=
\sum p_i dq_i - \sum P_idQ_i + (H-H')dt
\tag{5.3.2-4}
\]
となり、次の関係式が得られます。
\[
\begin{eqnarray}
p_i
& = &
\frac{\partial F}{\partial q_i}
\\
\dot{P_i}
& = &
- \frac{\partial F}{\partial Q_i}
\\
H'
& = &
H + \frac{\partial F}{\partial t}
\end{eqnarray}
\tag{5.3.2-5}
\]
この場合、関数Fは2s個の座標q、Qを用いてF(q,Q,t)で表すことができます。
さらに(5.3.2-5)式によって、元の座標に基づく変数(p,q)と新たな座標に基づく変数(P,Q)を連結し、さらに2つのハミルトン方程式間の関係も同時に与えます。
このような結果から、関数Fを“母関数”と呼ぶのはまさにふさわしい、と言えると思います。
また、母関数はq、Qだけでなく、q、Pでも表すことができます。 この場合、(5.3.2-4)式を変数変換(ルジャンドル変換)しなければなりませんが、結果だけを記せば、
\[
\begin{eqnarray}
p_i
& = &
\frac{\partial W}{\partial q_i}
\\
\dot{P_i}
& = &
- \frac{\partial W}{\partial P_i}
\\
H'
& = &
H + \frac{\partial W}{\partial t}
\end{eqnarray}
\tag{5.3.2-6}
\]
として同じような関係が得られます。
さて、(5.3.2-5)式、(5.3.2-6)式からもわかるように、母関数が時間を陽に含まないとき、新旧のハミルトニアンは等しくなります(H’=H)。 つまり、H(p,q)は正準変換において単純にH’(P,Q)と中身を置き換えればよいことがわかります。 さらに、変換によって得られたP、Qは運動量とか座標に縛られることなく、物理的概念から解放された単なる“量”として扱えます。理由は単純で、
- (5.3.1-2)式の変換式を満足しさえすればよいこと
- P、Qにはそれぞれ独立なp、qが含まれていること (例えば、Qi=piだったりPi=qiだったり...)
5.3.3.ポアソン括弧の条件
作成中です。5.4.位相空間
5.4.1.位相空間
ハミルトニアンHはs個の座標qとs個の運動量pを独立変数として扱った関数です(時間を陽に含めばさらにtも)。 これら2s個の変数を座標軸とした2s次元空間を位相空間と呼びます。 このとき、Hはq、pの関数であることから、位相空間内のどこかに点として存在します。 さらにq、pは変数であることから、その点は位相空間内に軌跡を描きます。 この軌跡をトラジェクトリと呼びます。 今、運動が二次元以上の空間で行われると、位相空間は四次元となり、幾何学的に描くことはできません。 このような曲面を超曲面と呼びます。5.4.2.位相空間内の運動
ここでは一つの運動として一次元調和振動を例に挙げ、その運動が位相空間内でどのように表現されるかについて見ていきます。 なお、ハミルトニアンHは時間を陽に含まず、q、pは一次元であるとします。今、Hは時間を陽に含まないため、(5.1.2-2)式を用いて次のようになります。
\[
\frac{dH}{dt}
=
0
\ \leftrightarrow \
\frac{\partial W}{\partial q_i}
H
=
T+U
=
E(const)
\tag{5.4.2-1}
\]
また、ハミルトン方程式(5.1.1-9)式から
\[
\begin{eqnarray}
\Delta q
& = &
\frac{\partial H}{\partial p} \Delta t
\\
\Delta p
& = &
- \frac{\partial H}{\partial q} \Delta t
\end{eqnarray}
\tag{5.4.2-2}
\]
となり、質点は微小時間Δtの間に位相空間内をΔq、Δpだけ移動します。
一次元調和振動は、次のような関係で表現されます。
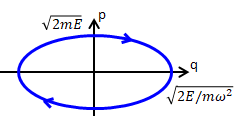
\[
\frac{1}{2}mv^2 + \frac{1}{2}m\omega^2x^2
=
\frac{1}{2m}p^2 + \frac{m\omega^2x^2}{2}
=
E(const)
\\
\\
\leftrightarrow \
\frac{1}{2mE} \ p^2 + \frac{x^2}{2E/m\omega^2}
=
1
\tag{5.4.2-3}
\]
図5.4.2-1 位相空間
図のように一次元調和振動はqp位相空間内で閉曲線(楕円)を描きます。(5.4.2-2)式の符号に注意すると、Hがtを陽に含まないことから、時間がΔt進むにつれ、前述の楕円軌道上を少しずつ時計まわりに移動します。 時計まわりである理由は(5.4.2-2)式の符号によります。 このとき、座標が決まれば運動量が決まり、また逆に運動量が決まれば座標が決まる、という関係、つまり座標と運動量のどちらか一方が決まればその運動が確定してしまう、という結果が得られます。 さらに、系のエネルギーEが変われば、この楕円が相似形で大きくなったり、小さくなったりし、楕円同士が交わることはありません。 これは同時刻に位相空間内のある1点を通る2つ以上の運動経路は存在しないことを意味します。 この結果は何も一次元調和振動に限ったことではなく、もっと一般的な運動にも拡張でき、自由度を増やしても適用できます(絵として描くのはできなくなりますが...)。
このように、ハミルトニアンと位相空間を用いて幾何学的に力学的状態を議論すると、運動の性質が把握しやすい、という利点があります。
ちなみに、一つの種類の変数(例えば座標q1、q2、…、qs)だけで構成される空間を配位空間と呼び、直交座標だけで表現する場合は、通常の私たちが暮らす空間と一致します。
5.4.3.リウビルの定理
前節では、自由度を2とした系で運動の記述を行いましたが、ここでは自由度を2sに拡張します。 系の移動の際に生じる位相空間内の微小体積を次のように表し、\[
d\Gamma
=
dq_1 \cdots dq_s dp_1 \cdots dp_s
\tag{5.4.3-1}
\]
これを位相空間のある領域にわたって積分した体積を考えます。
\[
\int d\Gamma
=
\int \cdots \int dq_1 \cdots dq_s dp_1 \cdots dp_s
\tag{5.4.3-2}
\]
変数p、qから変数P、Qへの正準変換が行われるとき、多重積分(5.4.3-2)の変数変換はヤコビアン
\[
\frac{\partial (Q_1, \cdots, Q_s, P_1, \cdots, P_s) \ \ }{\partial (q_1, \cdots, q_s, p_1, \cdots, p_s) \ \ }
=
\begin{vmatrix}
\frac{\partial Q_1}{\partial q_1} & \cdots & \frac{\partial Q_1}{\partial q_s} & \frac{\partial Q_1}{\partial p_1} & \cdots & \frac{\partial Q_1}{\partial p_s}
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial Q_s}{\partial q_1} & \cdots & \frac{\partial Q_s}{\partial q_s} & \frac{\partial Q_s}{\partial p_1} & \cdots & \frac{\partial Q_2}{\partial p_s}
\\
\frac{\partial P_1}{\partial q_1} & \cdots & \frac{\partial P_1}{\partial q_s} & \frac{\partial P_1}{\partial p_1} & \cdots & \frac{\partial P_1}{\partial p_s}
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial P_s}{\partial q_1} & \cdots & \frac{\partial P_s}{\partial q_s} & \frac{\partial P_s}{\partial p_1} & \cdots & \frac{\partial P_s}{\partial p_s}
\end{vmatrix}
\tag{5.4.3-3}
\]
によって行われます。
\[
\begin{eqnarray}
\int \cdots \int dQ_1 & \cdots & dQ_s dP_1 \cdots dP_s
\\
& = &
\int \cdots \int
\frac{\partial (Q_1, \cdots, Q_s, P_1, \cdots, P_s) \ \ }{\partial (q_1, \cdots, q_s, p_1, \cdots, p_s) \ \ }
dq_1 \cdots dq_s dp_1 \cdots dp_s
\end{eqnarray}
\tag{5.4.3-4}
\]
今、変数P、Qは正準変換によるので、ヤコビアンは次のように変形できます。
\[
\begin{eqnarray}
\frac{\partial (Q_1, \cdots, Q_s, P_1, \cdots, P_s) \ \ }{\partial (q_1, \cdots, q_s, p_1, \cdots, p_s) \ \ }
=
\frac{\quad \frac{ \partial (Q_1, \cdots, Q_s, P_1, \cdots, P_s) \ \ }{\partial (q_1, \cdots, q_s, P_1, \cdots, P_s) \ \ } \quad }
{ \quad \frac{\partial (q_1, \cdots, q_s, p_1, \cdots, p_s) \ \ }{\partial (q_1, \cdots, q_s, P_1, \cdots, P_s) \ \ } \quad }
\end{eqnarray}
\tag{5.4.3-5}
\]
ここで、P、Q、p、qのうち任意の2つを独立変数として扱うことができるので、ここではP、qを独立変数として扱います。
そこでまずは分子をそれぞれ変形していきます。
\[
\begin{eqnarray}
\frac{ \partial (Q_1, \cdots, Q_s, P_1, \cdots, P_s) \ \ }{\partial (q_1, \cdots, q_s, P_1, \cdots, P_s) \ \ }
& = &
\begin{vmatrix}
\frac{\partial Q_1}{\partial q_1} & \cdots & \frac{\partial Q_1}{\partial q_s} & \frac{\partial Q_1}{\partial P_1} & \cdots & \frac{\partial Q_1}{\partial P_s}
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial Q_s}{\partial q_1} & \cdots & \frac{\partial Q_s}{\partial q_s} & \frac{\partial Q_s}{\partial P_1} & \cdots & \frac{\partial Q_2}{\partial P_s}
\\
\frac{\partial P_1}{\partial q_1} & \cdots & \frac{\partial P_1}{\partial q_s} & \frac{\partial P_1}{\partial P_1} & \cdots & \frac{\partial P_1}{\partial P_s}
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial P_s}{\partial q_1} & \cdots & \frac{\partial P_s}{\partial q_s} & \frac{\partial P_s}{\partial P_1} & \cdots & \frac{\partial P_s}{\partial P_s}
\end{vmatrix}
\\
& = &
\begin{vmatrix}
\frac{\partial Q_1}{\partial q_1} & \cdots & \frac{\partial Q_1}{\partial q_s} & \frac{\partial Q_1}{\partial P_1} & \cdots & \frac{\partial Q_1}{\partial P_s}
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial Q_s}{\partial q_1} & \cdots & \frac{\partial Q_s}{\partial q_s} & \frac{\partial Q_s}{\partial P_1} & \cdots & \frac{\partial Q_2}{\partial P_s}
\\
0 & \cdots & 0 & 1 & \cdots & 0
\\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots
\\
0 & \cdots & 0 & 0 & \cdots & 1
\end{vmatrix}
\\
& = &
\begin{vmatrix}
A & B
\\
O & E
\end{vmatrix}
\\
& = &
|A|
\end{eqnarray}
\tag{5.4.3-6}
\]
この行列式は、小行列に分解していくことで最終的に次の形になります。
\[
|A|
=
\begin{vmatrix}
\frac{\partial Q_1}{\partial q_1} & \cdots & \frac{\partial Q_1}{\partial q_s}
\\
\vdots & \ddots & \vdots
\\
\frac{\partial Q_s}{\partial q_1} & \cdots & \frac{\partial Q_s}{\partial q_s}
\end{vmatrix}
=
\frac{ \partial (Q_1, \cdots, Q_s) \ \ }{\partial (q_1, \cdots, q_s) \ \ }
\tag{5.4.3-7}
\]
さらに、母関数を用いて書き直すと、
\[
\frac{ \partial (Q_1, \cdots, Q_s) \ \ }{\partial (q_1, \cdots, q_s) \ \ }
=
\begin{vmatrix}
\frac{\partial^2 W}{\partial q_1 \partial P_1} & \cdots & \frac{\partial^2 W}{\partial q_s \partial P_1}
\\
\vdots & \ddots & \vdots
\\
\frac{\partial^2 W}{\partial q_1 \partial P_s} & \cdots & \frac{\partial^2 W}{\partial q_s \partial P_s}
\end{vmatrix}
\tag{5.4.3-8}
\]
同様に分母も行うと、
\[
\begin{eqnarray}
\frac{\partial (q_1, \cdots, q_s, p_1, \cdots, p_s) \ \ }{\partial (q_1, \cdots, q_s, P_1, \cdots, P_s) \ \ }
& = &
\frac{ \partial (P_1, \cdots, P_s) \ \ }{\partial (p_1, \cdots, p_s) \ \ }
\\
\\
& = &
\begin{vmatrix}
\frac{\partial^2 W}{\partial q_1 \partial P_1} & \cdots & \frac{\partial^2 W}{\partial q_s \partial P_1}
\\
\vdots & \ddots & \vdots
\\
\frac{\partial^2 W}{\partial q_1 \partial P_s} & \cdots & \frac{\partial^2 W}{\partial q_s \partial P_s}
\end{vmatrix}
\end{eqnarray}
\tag{5.4.3-9}
\]
となり、結局ヤコビアンは“1”になり、(5.4.3-2)式は、
\[
\begin{eqnarray}
\int \cdots \int dQ_1 & \cdots & dQ_s dP_1 \cdots dP_s
\\
& = &
\int \cdots \int dq_1 \cdots dq_s dp_1 \cdots dp_s
\end{eqnarray}
\tag{5.4.3-10}
\]
となります。
この式の意味は、正準変換において位相空間の形は変わっても体積は不変に保たれることを意味します。
これをリウビウの定理と呼びます。


