4．4．渦の定理
4．4．1．ケルビンの循環定理
完全流体では、流体とともに動く任意の閉曲線Cに沿った循環は時間的に不変です。 これをケルビンの循環定理と呼びます。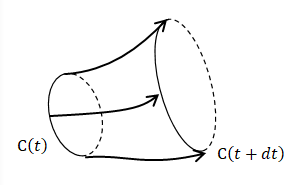
ケルビンの循環定理を証明するため、Cに沿う循環の時間変化について見ていきます。
\[
\begin{align}
\frac{d \Gamma}{dt}
& =
\frac{d}{dt}\oint_C \boldsymbol{v} \cdot d \boldsymbol{l}
\\
& =
\oint_C \frac{d \boldsymbol{v}}{dt} \cdot d \boldsymbol{l}
+ \oint_C \boldsymbol{v} \cdot \frac{d}{dt} (d \boldsymbol{l})
\end{align}
\tag{4.4.1-1}
\]
上式右辺第一項は、オイラーの式（4.3-5）とストークスの定理により
\[
\begin{align}
\oint_C \frac{d \boldsymbol{v}}{dt} \cdot d \boldsymbol{l}
& =
\oint_C -(\mathrm{grad} h) \cdot d \boldsymbol{l}
\\
& =
\oint_C -\mathrm{rot}(\mathrm{} h) \cdot d \boldsymbol{S}
\end{align}
\]
となります。
また、線素ベクトルは位置ベクトルを用いて\( d \boldsymbol{l} = \boldsymbol{r_2} - \boldsymbol{r_1} \)で表せるので、
\[
\frac{d}{dt}(d \boldsymbol{l})
=
\frac{d}{dt}(\boldsymbol{r_2} - \boldsymbol{r_1})
=
\boldsymbol{v_2} - \boldsymbol{v_1}
=
d \boldsymbol{v}
\]
とできます。よって右辺第二項は
\[
\oint_C \boldsymbol{v} \cdot \frac{d}{dt} (d \boldsymbol{l})
=
\oint_C \boldsymbol{v} \cdot d \boldsymbol{v}
=
\oint_C d \left( \frac{v^2}{2} \right)
\]
となります。
この積分は、開始点と終了点の速度\( v_s,v_e \)のみで決まりますが、閉曲線で積分しているため\( v_s=v_e \)であり、
\[
\oint_C d \left( \frac{v^2}{2} \right) = 0
\]
になります。
以上により、Cに沿う循環は時間に対し不変となることが証明できました。
\[
\frac{d \Gamma}{dt} = 0
\tag{4.4.1-2}
\]
4．4．2．ラグランジュの渦定理
完全流体では渦度は発生も消滅もしません。 つまり、- 渦あり流れは渦あり流れのまま
- 渦なし流れは渦なし流れのまま
4．4．3．ヘルムホルツの渦定理
完全流体では、1つの渦管は1つの渦管として保存され、その強さは一定になります。 これをヘルムホルツの渦定理と呼びます。この証明に先立ち、渦面とその保存について見ていきます。
渦面とは、渦線によって張られた曲面です。
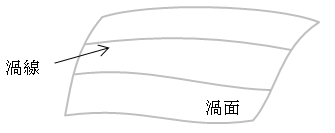
図4.4.3-1 渦面
ここで、ある時刻tで張られた渦面S上に任意の閉曲線Cをとると、その循環は\[
\Gamma(C)
=
\oint_C \boldsymbol{v} \cdot d \boldsymbol{l}
=
\oint_S \boldsymbol{\omega} \cdot d \boldsymbol{S}
\]
となります。
何故なら渦線は閉曲線Cを面外方向につらぬかないためです。
また時間\( \Delta t \)後、閉曲線CがC'に移ったとし、C'によって張られた曲面をS'とします。
このときCとC'の循環の間には、ケルビンの循環の定理によって\( \Gamma(C) = \Gamma(C') = 0 \)が成り立ちます。
C'はCを適当に選ぶことで曲面S'上で任意にとれます。 さらに\( \Gamma(C') = 0 \)から渦線は曲面S'上にのっており、S'は渦面です。 以上の結果、渦面は流体の運動に伴って1つの渦面として保存されます。 これを渦管に適用します。
渦管の側面は渦線によって張られる局面なので渦面となります。
そこで、渦管の側面上を一周するような閉曲線Cを考えると、ケルビンの循環定理によってCに沿う循環は時間に対し不変（一定）となります。 これは渦管の強さが不変であることを意味しています（2.3.4節参照）。
循環の断面積を無限小にすると渦管は渦糸となって、その強さは渦糸の断面積を\( \sigma \)とおいて
\[
d \Gamma = \omega \sigma
\tag{4.4.3-1}
\]
で表せます。
ここで、渦糸の線素\( d \boldsymbol{l} \)を用いてその体積は\( \sigma d \boldsymbol{l} \)、質量\( \rho \sigma d \boldsymbol{l} \)はとなります。
質量保存則（連続の式）から渦糸の質量\( \rho \sigma d \boldsymbol{l} \)は一定に保たれ、さらにヘルムホルツの渦定理から渦糸の循環\( d \Gamma \)も一定に保たれます。
従って、
\[
\frac{\rho d \boldsymbol{l}}{\omega} = const
\tag{4.4.3-2}
\]
の関係が得られます。
特に完全流体が非圧縮（\( \rho = const \)）の場合、渦糸の伸び縮みに対して渦度は比例します。
- 渦糸が伸びる→渦度大
- 渦糸が縮む→渦糸小
