2.4.渦なし流れ
2.4.1.領域の連結性
いきなりよくわからない言葉がでてきましたが、渦なし流れの特徴をつかむ上で大事な内容になります。 ここの厳密な話は数学の位相幾何学(トポロジー)という分野になりますが、ここで扱うのはそのさわりを使って流体内に物体があるかどうかを、流体内の領域に穴があるかないかで判別する、といったイメージを持っていただければ十分です。流体内に領域Dをとり、D内にとった任意の閉曲線Cについて考えます。 Dに穴がない場合、Cを連続的に縮めるとD内の1点に収束します。 それに対し、Dに穴がある場合、Cの取り方によっては穴が邪魔して1点に収束できません。
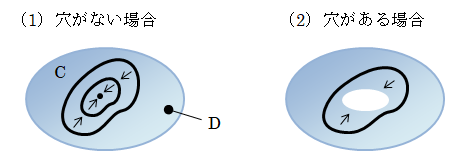
図2.4.1-1 閉曲線の縮め方
このように、D内の任意の閉曲線がすべて1点に縮められるとき、領域Dは単連結である、といい、それ以外は多重連結である、といいます。 多重連結については、D内にn-1個の切断を適切に入れると単連結にでき、この領域をn重連結と呼びます。
図2.4.1-2 連結領域の例
以上の内容が実際の流体の運動とどうつながるのか?というと、例えば川の流れをイメージすると理解しやすいと思います。
図2.4.1-3 連結領域の例
Digipot様(https://www.digipot.net/?p=1457)のフリー素材を利用しています。
この岩等で生じる流れの変化のような、流体内に置かれた固体まわりの流れを考察するために、領域の連結性の概念は必要となります。
2.4.2.多重連結の循環
この章では、渦なし流れを扱っていることに注意します。領域Dが単連結なら、D内の任意の閉曲線Cに沿う循環Γは、(2.3.3-2)式により常に0になります。
\[
\Gamma (C)
=
\oint_{S} \boldsymbol{\omega} \cdot d\boldsymbol{S}
\tag{2.4.2-1}
\]
単連結内の任意の閉曲線は1点収束するので、そのような閉曲線の循環は0になることがわかります。
次に、Dが二重連結の循環を考えます。
準備として、D内の任意の2点A、B間の速度積分を次のように表します。
\[
I(ACB)
=
\int_{ACB} \boldsymbol{v} \cdot d \boldsymbol{l}
\tag{2.4.2-2}
\]
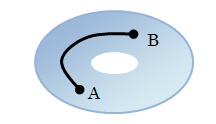 、D内に穴を囲う二つの閉曲線C、C'をとります。
さらに、C、C'をつなく直線AA'をとれば、閉曲線ACAA'C'A'は1点収束するので、その循環は0になります。
従って、
、D内に穴を囲う二つの閉曲線C、C'をとります。
さらに、C、C'をつなく直線AA'をとれば、閉曲線ACAA'C'A'は1点収束するので、その循環は0になります。
従って、
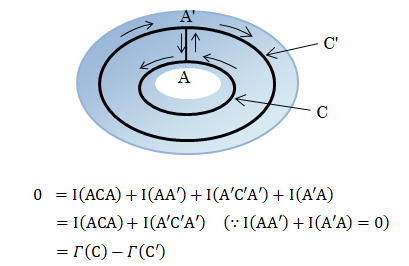 が得られ、D内の流れが静止していなければ一般に\( \Gamma(C)=\Gamma(C')≠0 \)となります。
さらに、Dを一か所切断すると単連結になります。
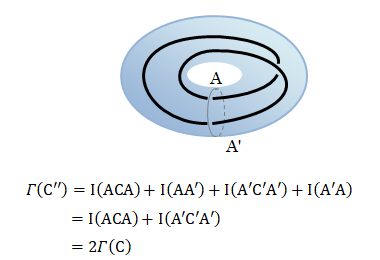
この切断を二回横切る閉曲線C''の循環を考えます。
切断を一回だけ横切る閉曲線Cの循環を\( \Gamma(C) \)とし、切断を反時計まわりに横切るときを“+”、その逆を“-”と定義します。
すると、\( \Gamma(C'') \)は次のようになります。
が得られ、D内の流れが静止していなければ一般に\( \Gamma(C)=\Gamma(C')≠0 \)となります。
さらに、Dを一か所切断すると単連結になります。
この切断を二回横切る閉曲線C''の循環を考えます。
切断を一回だけ横切る閉曲線Cの循環を\( \Gamma(C) \)とし、切断を反時計まわりに横切るときを“+”、その逆を“-”と定義します。
すると、\( \Gamma(C'') \)は次のようになります。
 また、次のような閉曲線C''をとれば
また、次のような閉曲線C''をとれば
 となり、\( \Gamma(C'') \)は\( \Gamma(C) \)の切断を横切る方向を考慮した回数倍となることがわかります。
となり、\( \Gamma(C'') \)は\( \Gamma(C) \)の切断を横切る方向を考慮した回数倍となることがわかります。
D内の穴の番号を添字\( i=1,2,\cdots,n \)とし、また、それに応じた切断を閉曲線が通過する回数について、前述の符号を考慮して\( p_i \)とします (反時計回りに3回通過すれば\( p_i=3 \)、時計回りに5回、反時計回りに3回通過すれば\( p_i=-5+3=-2 \))。 さらに、各穴のまわりの循環を\( \Gamma_i \)とすると、
\[
\Gamma (C)
=
\sum_{i=1}^{n} p_i \Gamma_i
\tag{2.4.2-3}
\]
が得られます。なお\( \Gamma_i \)を循環定数と呼びます。
一般に、多重連結において渦なし流れの循環は0でないことがわかります。
2.4.3.速度ポテンシャル
渦なし流れ、つまり渦度ωが0であれば流体要素の自転はありません。このとき、(2.3.1-1)式は\[
\boldsymbol{\omega}
=
\mathrm{rot} \boldsymbol{v}
=
\boldsymbol{0}
\tag{2.4.3-1}
\]
となります。微分演算子の回転rotの特徴として
\[
\mathrm{rot} (\mathrm{grad} \Phi)
=
\boldsymbol{0}
\tag{2.4.3-2}
\]
を満たす位置ベクトル\( \boldsymbol{r} \)を変数とするスカラー関数\( \Phi(\boldsymbol{r}) \)が存在します。
この\( \Phi(\boldsymbol{r}) \)を速度ポテンシャルと呼びます。
また、二つの式から流速ベクトル\( \boldsymbol{v} \)は速度ポテンシャル\( \Phi(\boldsymbol{r}) \)の勾配として表すことができます。
\[
\boldsymbol{v}
=
\mathrm{grad} \Phi
\tag{2.4.3-3}
\]
この速度ポテンシャルに基づく循環の性質は単連結と多重連結で異なります。
その違いについて、それぞれで見ていくことにします。
(1)領域Dが単連結の渦なし流れ
D内の任意の閉曲線Cに沿う循環は、Dが単連結で\( \boldsymbol{\omega} = 0 \)の条件により常に0です (多重連結ではこうはなりません)。\[
\Gamma (C)
=
\oint_{C} \boldsymbol{v} \cdot d \boldsymbol{l}
=
\oint_{S} \boldsymbol{\omega} \cdot d \boldsymbol{S}
\]
ここで速度ポテンシャル\( \Phi(\boldsymbol{r}) \)は、1つの任意定数に対して1つの曲面\( \Phi(\boldsymbol{r}) = const \)を与えます。
この曲面を等ポテンシャル面と呼びます。
速度ポテンシャルの特徴として、次のものが挙げられます。
a)等ポテンシャル面は流線と直交する
b)速度ポテンシャルは一価関数である
a)等ポテンシャル面と流線が直交することの証明は次の通りです。
等ポテンシャル面上に任意の曲線Sをとり、それ上の任意の点rを媒介変数\( s \)を用いて表すと、次のようになります。
\[
\boldsymbol{r}(s)
=
\left(
\begin{array}{c}
x(s)
\\
y(s)
\\
z(s)
\end{array}
\right)
\]
この点は\( \Phi(\boldsymbol{r}) = const \)を満たすので、
\[
\begin{align}
\frac{d \Phi}{ds}
& =
\frac{\partial \Phi}{\partial x} \frac{dx}{ds}
+\frac{\partial \Phi}{\partial y} \frac{dy}{ds}
+\frac{\partial \Phi}{\partial z} \frac{dz}{ds}
\\
& =
\mathrm(grad) \Phi \cdot \frac{d \boldsymbol r}{ds}
\\
& =
0
\end{align}
\]
となります。\( \mathrm{grad} \Phi \)は\( \boldsymbol{v} \)、\( d\boldsymbol{r}/ds \)は曲線Sの接線ベクトルであるから、\( \boldsymbol{v} \)と曲線Sは必ず直交します。
さらにSは等ポテンシャル面\( \Phi \)上で任意なため\( \boldsymbol{v} \)と\( \Phi \)も直交します。
つまり、流線と等ポテンシャル面は直交します。
次に、b)速度ポテンシャルが一価関数であることを証明します。
2.4.2節と同じように、D内に任意の二点をA、Bをとり、A、Bを結ぶ曲線Cに沿う速度積分を計算すると、
\[
\begin{align}
I(ACB)
& =
\int_{A}^{B} \boldsymbol{v} \cdot d\boldsymbol{l}
\\
& =
\int_{A}^{B} \frac{\partial \Phi}{\partial x}dx
+\frac{\partial \Phi}{\partial y}dy
+\frac{\partial \Phi}{\partial z} dz
\\
& =
\left[
\Phi
\right]_{\ B}^{\ A}
\\
& =
\Phi(B) - \Phi(A)
\end{align}
\]
となり、速度積分I(ACB)は経路Cに依らず点A、Bの位置のみで決まります。
この性質から、スカラー関数\( \Phi \)がポテンシャルであることになります。
(2)領域Dが多重連結の渦なし流れ
D内の任意の二点A、Bをとり二本の曲線をとります。 一つはD内で任意にとった曲線C、もう一つはD内に切断を入れたとき切断を通らない曲線C'とします。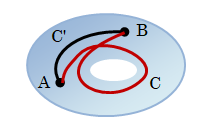 C'に沿う速度積分は(1)単連結領域で見たように、経路C'には依らずBの位置のみで決まる一価関数となります。
それに対しCに沿う速度積分は、I(ACBC'A)が閉曲線に対する速度積分であることを考慮にいれて、次のようになります。
C'に沿う速度積分は(1)単連結領域で見たように、経路C'には依らずBの位置のみで決まる一価関数となります。
それに対しCに沿う速度積分は、I(ACBC'A)が閉曲線に対する速度積分であることを考慮にいれて、次のようになります。
\[
I(ACBC'A)=I(ACB)+I(BC'A)
\]
ところで、I(ACBC'A)は前節により\( \sum p_i \Gamma_i \)で表せるので、
\[
I(ACB)
=
I(AC'B) + \sum p_i \Gamma_i
\]
となります。I(AC'B)はBの位置のみで決まる一価関数であるのに対し、I(ACB)はそれプラス循環定数の整数倍だけの多価性を持つことになります。


