レイノルズ方程式
1.レイノルズ方程式
レイノルズ方程式とは、2つの固体面にはさまれた薄い流体膜(例えば油膜など)に発生する圧力分布を求めるものです。 ただし、流体膜は次の前提条件を満足しなければなりません。- 流体力学が適用できるほど十分厚い
- レイノルズ仮定が成り立つほど十分薄い
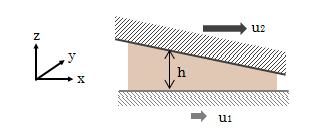
図1-1 流体膜モデル
なお、上述のレイノルズ仮定とは次のようなものです。- 層流
- 非圧縮性
- 粘性係数一定
- 重力、慣性力は粘性力に比べ無視できる
- 油膜厚さ方向(z)の圧力変化はない
- 流体と固体の間に滑りはない
- 流体の速度変化率の面内成分(x,y)は、面外成分(z)に対して無視できる
\[
\rho \frac{\partial v_i}{\partial t} + \rho v_k \frac{\partial v_i}{\partial x_k}
=
-\frac{\partial P}{\partial x_k} + \eta \frac{\partial^2 v_i}{\partial x_k^2} + F_i
\tag{1-1}
\]
上式は、アインシュタインの規約に基づく成分表示になります。
まず、レイノルズ仮定d)より慣性項を表わす(1-1)式左辺は“0”になります。
次に、右辺のFは流体に作用する外力であり、一般には重力によるものが主となります。
これについても仮定d)により“0”と出来、(1-1)式は次のようになります。\[
0
=
-\frac{\partial P}{\partial x_k} + \eta \frac{\partial^2 v_i}{\partial x_k^2}
\tag{1-2}
\]
また、仮定g)より速度変化率の面内成分は無視できることから、例えばx成分の粘性項について具体的に示すと以下のとおりになります。\[
\frac{\partial^2 v_x}{\partial x^2}+\frac{\partial^2 v_x}{\partial y^2} +\frac{\partial^2 v_x}{\partial z^2}
\simeq
\frac{\partial^2 v_x}{\partial z^2}
\tag{1-3}
\]
以上の結果、(1-2)式のx,y成分は次のように書き換えられます。\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{\partial P}{\partial x} \simeq \eta \frac{\partial^2 v_x}{\partial z^2}
\\
\displaystyle \frac{\partial P}{\partial y} \simeq \eta \frac{\partial^2 v_y}{\partial z^2}
\end{array}
\right.
\end{eqnarray}
\tag{1-4}
\]
上式を積分することで、流体膜のある高さにおける面内方向の流速を求めることが出来ます。
ここでは、x成分について具体的に示します(y成分も同様に定まります)。
なお、積分の実行において、仮定e)を踏まえておく必要があります(Pはzに対して一定)。\[
\begin{eqnarray}
\frac{\partial v_x}{\partial z}
& = &
\int \frac{1}{\eta} \frac{\partial P}{\partial x} dz
=
\frac{1}{\eta} \frac{\partial P}{\partial x} z + c_1
\\
\\
v_x
& = &
\int \Bigl( \frac{1}{\eta} \frac{\partial P}{\partial x} z + c_1 \Bigr) dz
=
\frac{1}{2\eta} \frac{\partial P}{\partial x} z^2 + c_1 z + c_2
\end{eqnarray}
\tag{1-5}
\]
ここで、境界条件である仮定f)からz=0のときvx=u1、
z=hのときvx=u2を(1-4)式に適用して、\[
v_x
=
-\frac{1}{2\eta} \frac{\partial P}{\partial x} z (h-z)
+\left\{(1-\frac{z}{h})u_1+\frac{z}{h}u_2 \right\}
\tag{1-6}
\]
が得られます。この式の各項には次のような意味があります。
右辺第一項は、圧力勾配と膜厚方向の二次関数によって得られる流れであり、ポアズイユ流(圧力流れ)と呼びます。
第二項は固体2面の運動に基づく流れであり、クエット流せん断流れ)と呼びます。次に、連続の式(質量保存則)について考えます。仮定b)により流体膜の密度変化はないため、連続の式は以下で表わせます。
\[
\frac{\partial v_x}{\partial x} +
\frac{\partial v_y}{\partial y} +
\frac{\partial v_z}{\partial z}
=
0
\tag{1-7}
\]
これをz方向に対して0~hで定積分します。
なお、z=0でのvy=v1、vz=w1、z=hでのvy=v2、vz=w2とします。\[
\begin{eqnarray}
& &\int_0^h \Bigl( \frac{\partial v_x}{\partial x} +
\frac{\partial v_y}{\partial y} +
\frac{\partial v_z}{\partial z} \Bigr) dz
\\
\\
& = &
\frac{\partial}{\partial x}\int_0^h v_x dz
+ \frac{\partial}{\partial y}\int_0^h v_y dz
+(w_2-w_1)
\end{eqnarray}
\tag{1-8}
\]
(1-6)式(x,y成分とも)を上式に代入して計算すれば、以下の式が得られます。\[
\begin{eqnarray}
& & \frac{\partial}{\partial x} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial x} \Bigr) +
\frac{\partial}{\partial y} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial y} \Bigr)
\\
\\
& = &
6 \Bigl \{
(u_1-u_2)\frac{\partial h}{\partial x}
+ h\frac{\partial}{\partial x}(u_1+u_2)
+(v_1-v_2)\frac{\partial h}{\partial y}
+ h\frac{\partial}{\partial y}(v_1+v_2)
+2(w_2-w_1)
\Bigr \}
\end{eqnarray}
\tag{1-9}
\]
この式によって、座標(x,y)における流体膜の圧力を求めることができ、レイノルズ方程式と呼びます。
実際はもう少し簡単に書き換えることができます。
面内方向の流速は、座標をうまく設定することで一成分で表わせます
(例えばuとvの合成ベクトル方向をx軸ととれば、vを落とすことが出来ます)。
次に、仮定d)によって慣性項を無視していることから、固体片側を静止面とみることができ、
u1=w1=0として一般性を失いません。
以上をもとに仮定c)を考慮に入れ(1-9)式を次のように書き換えることが出来ます。\[
\frac{\partial}{\partial x} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial x} \Bigr) +
\frac{\partial}{\partial y} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial y} \Bigr)
=
6 \Bigl \{
-u_2\frac{\partial h}{\partial x}
+ h\frac{\partial u_2}{\partial x}
+2 w_2
\Bigr \}
\tag{1-10}
\]
なお、上式右辺は流体膜に圧力が生じる要因となっています。
右辺第一項は膜厚変化によって圧力が発生することを意味し、くさび効果と呼びます。
右辺第二項は固体に変位が生じ、面内速度が変化する際に圧力が生じることを意味し、
ストレッチ効果(伸縮効果)と呼びます。
右辺第三項は、膜厚が圧縮される方向に固体が移動する際に圧力が発生することを意味し、
スクイズ効果(絞り効果)と呼びます。最後に、固体が剛体ならばu2は面内のどの位置も一定であり、ストレッチ効果はなくなます。 その結果(1-10)式から第二項を取り除くことで、簡素化されたレイノルズ方程式が得られます。
\[
\frac{\partial}{\partial x} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial x} \Bigr) +
\frac{\partial}{\partial y} \Bigl( \frac{h^3}{\eta} \frac{\partial P}{\partial y} \Bigr)
=
6 \Bigl (
-u_2\frac{\partial h}{\partial x}
+2 w_2
\Bigr )
\tag{1-11}
\]
以上、レイノルズ方程式は前提条件が多く設けられており、その適用については注意が必要です。
流体膜が温度分布の影響等を受け密度や粘性変化を考慮しなければならない場合や、慣性項を無視できない場合などは、レイノルズ仮定をはずした一般化レイノルズ方程式を適用することになります。
一般化レイノルズ方程式については別途述べることにします。


