2.流れの表現
2.1.流れの記述法
流体の運動を記述する方法として次の二つがあります。(1)ラグランジュ法:質点系の考え方
流体要素を質点と捉えて、時間的に位置を追跡する見方です。流体要素の時間変化:\( \displaystyle \frac{d \boldsymbol{v}}{dt} \)
(2)オイラー法:場の考え方
流体内に固定された位置に着目し、その位置を通過する流体の時間的変化を追う見方となります。 天気予報で見る風や台風の予報図はこの表現方法によるものです。流体要素の時間変化:\( \displaystyle \frac{\partial \boldsymbol{v}}{\partial t} \)

図2.1-1 流れの記述法
2.2.流れの可視化
2.2.1.流線
流れの中の曲線で、その線上の任意の接線が流れの速度方向と一致するものを流線と呼びます。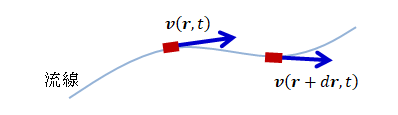
図2.2.1-1流線
流線上のある点での線素ベクトルを\( d \boldsymbol{l}=(dx,dy,dz) \)、その点での速度ベクトルを\( \boldsymbol{v} \)とすると\( \boldsymbol{v} \)と\( d \boldsymbol{l} \)は平行なため、\[
\boldsymbol{v} = c d \boldsymbol{l}
\]
が成り立ちます。各成分の関係を調べると
\[
\frac{dx}{v_x}
=
\frac{dy}{v_y}
=
\frac{dz}{v_z}
(=c)
\tag{2.2.1-1}
\]
が得られ、二つの独立した常微分方程式を与えるので、その解は次のように書けます。
\[
\begin{align}
& f_1(x,y,z,t)=c_1
\\
& f_2(x,y,z,t)=c_2
\end{align}
\tag{2.2.1-2}
\]
流線はこの2つの曲面上に存在することから、これらの交線として与えられます。
また(2.2.1-2)式はある時刻tでの流線を示すもので、通常時々刻々変化します。
それに対し定常流であれば(2.2.1-2)式は時間に対し不変となり場に固定されるので、その表現はオイラー的になります。
2.2.2.流跡線
1つの流体粒子が時間の経過とともに移動するときに描く軌跡を流跡線と呼びます。 この定義から明らかなように、その表現はラグランジュ的になります。 流体粒子が微小時間dtの間に流跡線に沿って\( d \boldsymbol{l}=(dx,dy,dz) \)動いたとすると、\[
\boldsymbol{l} = \boldsymbol{v} dt
\]
を満たします。各成分の関係を調べると
\[
\frac{dx}{v_x}
=
\frac{dy}{v_y}
=
\frac{dz}{v_z}
=
dt
\tag{2.2.2-1}
\]
が得られ、三つの独立した常微分方程式を与えるので、その解は次のように書けます。
\[
\begin{align}
& f_1(x,y,z,t)=c_1
\\
& f_2(x,y,z,t)=c_2
\\
& f_3(x,y,z,t)=c_3
\end{align}
\tag{2.2.2-2}
\]
この三つの式からtを消去すれば、tを含まない2つの曲面が得られます。
流跡線はその2つの曲面上に存在するので、その交線によって与えられます。
2.2.3.流脈線
流体中のある固定した点を時々刻々通過するすべての流体粒子が、ある時刻tで到達した点を連ねた曲線を流脈線と呼びます。 煙突の煙はまさに流脈線そのものといえます。
図2.2.3-1 流線・流跡線・流脈線
一般に、流線、流跡線、流脈線は一致しませんが、定常流の場合に限りこれらはすべて一致します。2.2.4.流管
流れの中に任意の閉曲線Cをとり、C上の各点を通る流線群から1つの管を作ることができます。 この管を流管と呼びます。 非定常流の場合流管は時々刻々変化するのに対し、定常流では流管の形は不変です(定常流の流線は不変)。 従って、定常流では流管と同じ管を流れているのと同等とみなせます。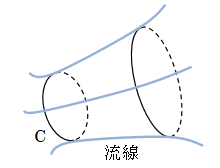
図2.2.4-1 流管
2.3.渦の表現
2.3.1.渦度
渦度は流れの局所的な自転を表すもので\[
\boldsymbol{\omega} = \mathrm{rot} \boldsymbol{v}
\tag{2.3.1-1}
\]
で定義されます。
渦度の大きさは自転の角速度の倍で、その方向は自転の向きと一致します。
渦度は他にも連続体ページ2.3.2節で示した回転テンソルをベクトルとして表したものでもあります。
2.3.2.渦線
流線(2.2.1節)が速度ベクトルvに対して定義されたのと同様に、渦度ベクトルωに対して渦線を定義します。ある時刻tにおいて流れの中に1本の曲線をとり、その各点で渦度ベクトルωが接線となるような曲線を渦線と呼びます。 渦線の線素ベクトルを\( d \boldsymbol{l} \)とすれば\( \boldsymbol{\omega} \)と\( d \boldsymbol{l} \)は平行であり、
\[
\boldsymbol{\omega} = c d \boldsymbol{l}
\]
が成り立ちます。各成分の関係を調べると
\[
\frac{dx}{\omega_x}
=
\frac{dy}{\omega_y}
=
\frac{dz}{\omega_z}
(=c)
\tag{2.3.2-1}
\]
が得られます。
流線のときと同様、これは二つの独立した常微分方程式を与え、その解は次のように書けます。
\[
\begin{align}
& g_1(x,y,z,t)=c_1
\\
& g_2(x,y,z,t)=c_2
\end{align}
\tag{2.3.2-2}
\]
渦線はこの2つの曲面上に存在することから、これらの交線として与えられます。
2.3.3.渦管・渦糸
流管同様、流れの中に任意の閉曲線Cをとり、C上の各点を通る渦線群から1つの管を作ることができます。 この管を渦管と呼びます。この渦管を定義した閉曲線Cの面積を極限まで小さくしたものを渦糸と呼びます。 渦糸は見かけ上渦糸と同じですが、渦線が単なる幾何学的な曲線であるのに対し、渦糸は面積重みの付いた曲線である、といえます。
2.3.4.循環
流体内にとった任意の閉曲線Cに沿っての流速vの積分をCに沿う循環と呼びます。\[
\Gamma
=
\oint_C \mathrm{rot} \boldsymbol{v} \cdot d \boldsymbol{l}
\tag{2.3.4-1}
\]
この積分はストークスの定理によって線積分から面積分に書き換えられます。
\[
\Gamma
=
\oint_C \mathrm{rot} \boldsymbol{v} \cdot d \boldsymbol{l}
=
\oint_S \boldsymbol{\omega} \cdot d \boldsymbol{S}
\tag{2.3.4-2}
\]
ここで、閉曲線Cに交わらず渦管を1周する別の閉曲線C'を取ります。
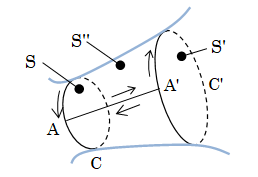
図2.3.4-1 流管
このとき、渦管上にはCで囲まれた面S、C'で囲まれた面S'、CとC'の間を結ぶ曲面S''の三つの面が作られます。 また、閉曲線C、C'上にそれぞれ1点A、A'をとります。 すると、円ACA→線AA'→円A'C'A'→線A'Aによって閉曲線C''が作れ、このC''に沿う循環が\[
\oint_{C''} \mathrm{rot} \boldsymbol{v} \cdot d \boldsymbol{l}
=
\oint_{S''} \boldsymbol{\omega} \cdot d \boldsymbol{S}
=
0
\]
を満たすことは、\( \boldsymbol{\omega} \)が渦管側面の法線と必ず直交することから明らかです。また、
\[
\begin{align}
\oint_{C''} \mathrm{rot} \boldsymbol{v} \cdot d \boldsymbol{l}
& =
\oint_C \boldsymbol{v} \cdot d \boldsymbol{l}
+ \int_{A}^{A'} \boldsymbol{v} \cdot d \boldsymbol{l}
+ \oint_{C'} \boldsymbol{v} \cdot d \boldsymbol{l}
+ \int_{A'}^{A} \boldsymbol{v} \cdot d \boldsymbol{l}
\\
& =
\oint_C \boldsymbol{v} \cdot d \boldsymbol{l}
+ \oint_{C'} \boldsymbol{v} \cdot d \boldsymbol{l}
\\
& =
0
\end{align}
\]
となるので、Cに沿う循環とC'に沿う循環は同じになります。
これは渦管を一周する循環が閉曲線Cの取り方に依らず一定であることを意味しています。
つまり、循環\( \Gamma \)はある時刻に決まった1本の渦管に固有の値であり、渦管の強さを表します。


