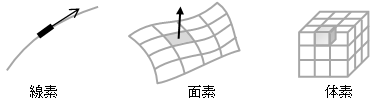
1.4.線素・面素・体素
線素は曲線の微小長さ要素を表します。 ベクトル\( d \boldsymbol{l} \)として扱い、その長さは微小長さ\( dl \)、方向は曲線の接線方向と一致します。面素は曲面の微小面積要素を表します。 ベクトル\( d \boldsymbol{S} \)として扱い、その大きさは微小面積\( dS \)、方向は面素の法線方向と一致します。
体素は領域の微小体積要素を表します。 これらは主に線積分、面積分、体積積分で用いられる概念です。
図1.4-1 線素・面素・体素
1.5.数学の準備
ここでは数学そのものの話ではなく、流体力学で頻出する公式や規則の紹介のみとします。なお、本サイトのパラメータについて、太字(例えば\( \boldsymbol{v} \)、\( \boldsymbol{r} \)など)をベクトル、標準字(例えば\( p \)、\( \rho \)など)をスカラーとして扱います。
1.5.1.テンソル
テンソルとは、端的に言えば複数のベクトル\( \boldsymbol{u},\boldsymbol{v},⋯ \)をスカラーに写す関数\( T(\boldsymbol{u},\boldsymbol{v},⋯) \)です。流体(連続体)力学で用いられるテンソルは、三次元ベクトルをスカラーに変換するものです。(1)テンソルの階数
例えば、空間座標の軸単位ベクトル\( e_x,e_y,e_z \)のうちの2つを変数とするテンソル関数\( T(e_i,e_j ) \)よって決まるスカラー量を次のように定義します。\[
T(e_i,e_j )=T_{ij}
\qquad
(i,j=x,y,z)
\]
すると、\( i,j \)の組み合わせによって9個の値が得られます。
\[
\begin{eqnarray}
\left(
\begin{array}{ccc}
t_{11} & t_{12} & t_{13}
\\
t_{21} & t_{22} & t_{23}
\\
t_{31} & t_{32} & t_{33}
\\
\end{array}
\right)
\end{eqnarray}
\]
このテンソル\( T \)は添字を二つ持つ成分で構成され、二階テンソルといいます。
添字が一つの成分で構成されるテンソルを一階テンソル、一般化して添字が\( n \)個のテンソルをn階テンソルと呼びます。
スカラーは0階テンソルとして扱われます。
(2)テンソルの縮約表記
同じ添え字があるときは、その添え字について和をとることにします。 目的は表記の簡素化です。\[
\begin{array}
v_j \frac{\partial v_i}{\partial x_j}
& =
\displaystyle \sum_{ j = x,y,z } v_j \frac{\partial v_i}{\partial x_j}
\\
& \displaystyle =
v_x \frac{\partial v_i}{\partial x}
+v_y \frac{\partial v_i}{\partial y}
+v_z \frac{\partial v_i}{\partial z}
\end{array}
\]
(3)ダイアド積
\[
\left(
\begin{array}{ccc}
a_1
\\
a_2
\\
a_3
\\
\end{array}
\right)
\otimes
\left(
\begin{array}{ccc}
b_1
\\
b_2
\\
b_3
\\
\end{array}
\right)
=
\begin{eqnarray}
\left(
\begin{array}{ccc}
a_1b_1 & a_1b_2 & a_1b_3
\\
a_2b_1 & a_2b_2 & a_2b_3
\\
a_3b_1 & a_3b_2 & a_3b_3
\\
\end{array}
\right)
\end{eqnarray}
\]
1.5.2.完全微分
関数\( f(x,y,z) \)について\[
df
=
\frac{\partial f}{\partial x}dx
+\frac{\partial f}{\partial y}dy
+\frac{\partial f}{\partial z}dz
\]
1.5.3.ベクトル微分
ベクトルの微分演算子としてナブラ演算子\( \nabla \)を次のように定義します。\[
\nabla
=
\left(
\begin{array}{ccc}
\displaystyle \frac{\partial}{\partial x}
\\
\displaystyle \frac{\partial}{\partial y}
\\
\displaystyle \frac{\partial}{\partial z}
\end{array}
\right)
\]
(1)勾配:grad
\[
\mathrm{grad} \Phi
=
\nabla \Phi
=
\left(
\begin{array}{ccc}
\displaystyle \frac{\partial \Phi}{\partial x}
\\
\displaystyle \frac{\partial \Phi}{\partial y}
\\
\displaystyle \frac{\partial \Phi}{\partial z}
\end{array}
\right)
\]
(2)発散:div
ベクトル関数\( \boldsymbol{A}(x,y,z) \)に対して\[
\mathrm{div} \boldsymbol{A}
=
\nabla \cdot \boldsymbol{A}
=
\frac{\partial A_x}{\partial x}dx
+\frac{\partial A_y}{\partial y}dy
+\frac{\partial A_z}{\partial z}dz
\]
(3)回転:rot
ベクトル関数\( \boldsymbol{A}(x,y,z) \)に対して\[
\mathrm{rot} A
=
\nabla \times A
=
\left(
\begin{array}{ccc}
\displaystyle \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z}
\\
\displaystyle \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x}
\\
\displaystyle \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}
\end{array}
\right)
\]
(4)ラプラシアン
関数\( \Phi(x,y,z) \)に対して\[
\Delta \Phi
=
\nabla^2 \Phi
=
\mathrm{div(grad} \Phi )
=
\frac{\partial^2 \Phi }{\partial x^2}
+\frac{\partial^2 \Phi }{\partial y^2}
+\frac{\partial^2 \Phi }{\partial z^2}
\]
(5)ベクトルで微分
関数\( \Phi(\boldsymbol{r}) \)に対して\[
\frac{d \Phi}{d \boldsymbol{r}}
=
\mathrm{grad} \Phi
=
\left(
\begin{array}{ccc}
\displaystyle \frac{\partial \Phi}{\partial x}
\\
\displaystyle \frac{\partial \Phi}{\partial y}
\\
\displaystyle \frac{\partial \Phi}{\partial z}
\end{array}
\right)
\]
ベクトル関数\( \boldsymbol{A}(\boldsymbol{r}) \)に対して
\[
\begin{align}
\frac{d \boldsymbol{A}(\boldsymbol{r})}{d \boldsymbol{r}}
& =
\mathrm{grad} \boldsymbol{A}
\\
& =
(
\mathrm{grad} A_x,
\mathrm{grad} A_y,
\mathrm{grad} A_z
)
\\
\\
& =
\left(
\begin{array}{ccc}
\displaystyle \frac{\partial A_x}{\partial x}
&
\displaystyle \frac{\partial A_x}{\partial y}
&
\displaystyle \frac{\partial A_x}{\partial z}
\\
\displaystyle \frac{\partial A_y}{\partial x}
&
\displaystyle \frac{\partial A_y}{\partial y}
&
\displaystyle \frac{\partial A_y}{\partial z}
\\
\displaystyle \frac{\partial A_z}{\partial x}
&
\displaystyle \frac{\partial A_z}{\partial y}
&
\displaystyle \frac{\partial A_z}{\partial z}
\end{array}
\right)
\end{align}
\]
(6)ベクトル演算子の公式
- \( \mathrm{div}(\Phi \boldsymbol{A}) = \Phi \mathrm{div} \boldsymbol{A} + \mathrm{grad} \Phi \cdot \boldsymbol{A} \)
- \( \mathrm{rot}(\Phi \boldsymbol{A}) = (\mathrm{grad} \Phi) \times \boldsymbol{A} + \Phi \mathrm{rot} \boldsymbol{A} \)
- \( \mathrm{div}(\boldsymbol{A} \times \boldsymbol{B}) = \boldsymbol{B} \cdot \mathrm{rot} \boldsymbol{A} - \boldsymbol{A} \cdot \mathrm{rot} \boldsymbol{B} \)
- \( \mathrm{rot}(\boldsymbol{A} \times \boldsymbol{B}) = ( \boldsymbol{B} \cdot \mathrm{grad} ) \boldsymbol{A} - ( \boldsymbol{A} \cdot \mathrm{grad} ) \boldsymbol{B} + \boldsymbol{A} ( \mathrm{div} \boldsymbol{B}) \)
- \( \mathrm{rot}(\mathrm{grad} \Phi) = 0 \)
- \( \mathrm{div}(\mathrm{rot} \Phi) = 0 \)
- \( \mathrm{rot}(\mathrm{rot} \boldsymbol{A}) = \mathrm{rot} ( \mathrm{div} \boldsymbol{A} ) - \mathrm{\Delta} \boldsymbol{A} \)
1.5.4.積分
ベクトル関数\( \boldsymbol{A} \)に対して、次の積分変換が成り立ちます。(1)ガウスの定理:面積分~体積積分の変換
領域Sの面積分~領域Sで囲まれた体積領域Vの体積積分の変換\[
\displaystyle \oint_S \boldsymbol{A} \cdot d \boldsymbol{S}
=
\displaystyle \int_V ( \mathrm{div} \boldsymbol{A} ) dV
\]
(2)ストークスの定理:線積分~面積分の変換
閉曲線Cに沿っての線積分~閉曲線Cで囲まれた領域Sの面積分の変換\[
\displaystyle \oint_C \boldsymbol{A} \cdot d \boldsymbol{r}
=
\displaystyle \oint_S ( \mathrm{rot} \boldsymbol{A} ) \cdot d \boldsymbol{S}
\]
(3)線積分が経路に依らない条件(積分が始点Pと終点Qのみで決まる条件)
\[
\mathrm{rot} \boldsymbol{A} = \boldsymbol{0}
\Leftrightarrow
\boldsymbol{A} = \mathrm{grad} \Phi
\Leftrightarrow
\displaystyle \int_{P}^{Q} \boldsymbol{A} \cdot d \boldsymbol{r}
=
\Phi(P) - \Phi(Q)
\]