歯車の設計
1.歯車の目的と種類
歯車の主な目的は“回転や動力の伝達”です。 歯車には、読んで字のごとく、歯が切ってあり、それらが噛み合うことによってその目的が達せられます。 よって、歯車の設計では、歯の形(諸元)を決定することが重要になります。 さて、歯車には様々な種類があり、その分類方法もいろいろあります。 そのうち本節では、用途に合わせた歯車の分類とその種類について記します。表1-1 用途に合わせた歯車の分類
| 軸 | 出力 方向 |
特殊要件 | 歯車種類 | 備考 | |
|---|---|---|---|---|---|
| 平行軸 | 反転 | 一般的 | 平歯車 (スパーギア) |
最も一般的な歯車 | |
| 高回転 静寂性 |
はすば歯車 (ヘリカルギア) |
平歯車と同じ工具で歯切り可能 | |||
| スラスト力 抑制 |
やまば歯車 | 製作困難 | |||
| 同一 | 一般的 | 内歯車 (インターナルギア) |
ギアボックス小型化 遊星歯車装置 |
||
| 高回転 静寂性 |
内はすば歯車 | ||||
| 軸同士の 連結 |
スプライン | ||||
| 直動 | 一般的 | (平)ラック | インボリュート歯形の基準となる寸法を決める | ||
| 高回転 静寂性 |
はすばラック | ||||
| 交差軸 | 減速比1:1 | マイタ歯車 | |||
| 一般的 | すぐばかさ歯車 (ベベルギア) |
歯車一対を決めて作るため、歯数が異なるとかみ合わない | |||
| 高回転 高負荷 |
まがりばかさ歯車 (スパイラルベベルギア) |
同上の問題 +製作困難 |
|||
| 食い違い軸 | 静寂性 | ねじ歯車 (スパイラルギア) |
はすば歯車の軸を変えたもの 低効率・小動力 |
||
| 大減速比 | ウォームギア | 逆転防止(条件による) | |||
| 高回転 高負荷 |
ハイポイド歯車 | まがりばかさ歯車の一種 | |||
KHK殿ホームページ:
http://www.khkgears.co.jp/gear_technology/basic_guide/KHK347.html

2.歯車の諸元と歯形
2.1.歯車の諸元
歯車の諸元については下記サイトでわかりやすく解説されていますので、そちらをご参照ください。KHK殿ホームページ
http://www.khkgears.co.jp/gear_technology/basic_guide/KHK353_2.html

また、歯車の用語については、以下のJISで規定されていますので、詳細はこちらを参照ください。
| JIS B 0102-1 | : | 歯車用語-第一部:幾何形状に関する定義 |
| JIS B 0102-2 | : | 歯車用語-第二部:ウォームギアの幾何形状に関する定義 |
| JIS B 0121 | : | 歯車記号-幾何学的データの記号 |
| JIS B 1701-1 | : | 円筒歯車-インボリュート歯車歯形 第1部:標準基準ラック歯形 |
| JIS B 1701-2 | : | 円筒歯車-インボリュート歯車歯形 第2部:モジュール |
| JIS B 1706-1 | : | すぐばかさ歯車-第1部:基準ラック |
| JIS B 1706-2 | : | すぐばかさ歯車-第2部:モジュール及びダイヤメトラルピッチ |
2.2.歯形曲線
歯形を描く曲線はいろいろありますが、特に- インボリュート曲線
- サイクロイド曲線
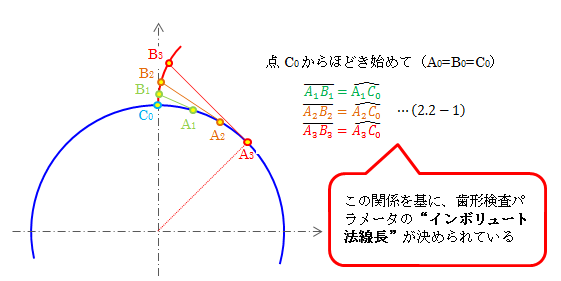
図2.2-1 インボリュート曲線
この関係性を用いれば、インボリュート曲線を関数化できます。 計算式はあえて掲載しませんが、回転変換を用いるだけで簡単に求められます(図2.2-3参照)。インボリュート曲線によって切られた歯形は、“歯車とラックの噛み合い関係”から得られます。 このインボリュート歯形を持つ歯車のことをインボリュート歯車と呼びます。 インボリュート歯形の創生方法は、下図のように、まず“歯車の噛み合いピッチ円接線(=歯切基準線)”と“ラックの噛み合いピッチ線(=ラック基準線)”を一致させます。 そして、ラックを歯車のピッチ円上の周速と一致する速度で動かせば、ラック側面が描く包絡線によってインボリュート曲線が描かれます。
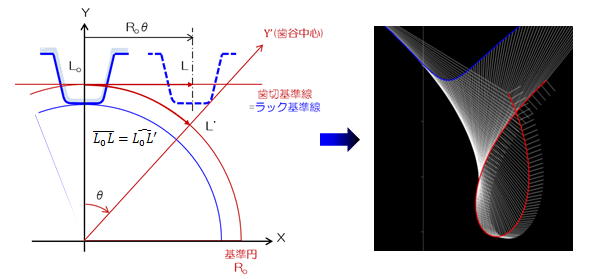
図2.2-2 ラック創生によるインボリュート曲線
この包絡線関数によってもインボリュート曲線を描画することができます (数式の立て方は、解析学の教科書を参考にしてみてください)。さらに転位歯車の場合、転位量が“+”ならばラックを転位量分歯車から離して、前述と同じように動かせば得られます。
さて、インボリュート歯形には次のような特徴があります。
- 取付軸間距離に多少の誤差があっても噛み合い精度は維持される
- 歯の生成が簡単で、歯形精度が得られやすい
- 同一工具で歯数の違う歯車を製作できる
ラックによって歯切りされる場合、歯元曲線も同様な座標変換によって得られます。 この場合、歯元曲線はトロコイド曲線となります。これについては当方で作成したソフトで描画可能です。
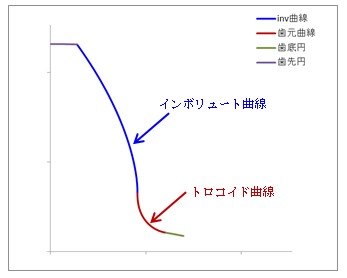
図2.2-3 インボリュート曲線と歯元曲線
2.3.歯の噛み合い
2.3.1.噛み合い率
歯車は、歯の噛み合いによってその目的が達せられることを1章で述べました。 この噛み合いについて定量的に評価する方法として、噛み合い率があります。 特に、次節でみるインボリュート歯車の噛み合い率は以下で求めることができます。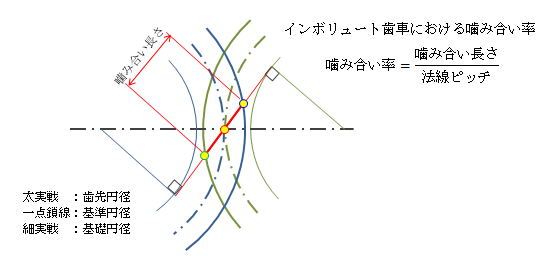
図2.3.1-1 インボリュート歯車の噛み合い率
噛み合い率は歯車の性能を決める上で重要な役割を担っており、静寂性、伝達トルク変化などに影響を与えます。 噛み合い率の設定は必ず1以上とし、一般的には1.2以上とるのが望ましいとされています。 噛み合い率が大きくなれば、それだけ歯形誤差の打ち消し合いが得られやすくなるので、騒音や伝達トルク変化に有利に働きます。 特に歯をねじったはすば歯車については、噛み合い率向上を狙っており、それによって静寂性が平歯車よりも向上します。2.3.2.すべり率
歯車の歯は、基準ピッチ円上では転がり接触、それ以外ではすべり接触となります。 すべりは摩擦に起因し、特にエネルギーを熱に変換することから伝達効率を落とす原因となります (熱の意味については、熱力学ページをご参照ください)。 そこで、このすべり度合を評価するものとして、すべり率σが定義されています。 これは互いの歯車の相対速度比に基づいて考えられたもので、\[
歯車1:\sigma_1 = \frac{d_2 - d_1}{d_1}
\\
歯車2:\sigma_2 = \frac{d_2 - d_1}{d_2}
\\
(d:歯車基準径)
\]
となります。


